Matemática
Inequação é uma desigualdade de elementos, portanto uma inequação - produto pode ser representada da seguinte forma:
h(x) . w(x) > 0
h(x) . w(x) < 0
h(x) . w(x) ≠ 0
h(x) . w(x) ≥ 0
h(x) . w(x) ≤ 0
Sendo que h e w estão representando qualquer função (elemento). Por exemplo:
Qual seriam os possíveis valores de x para que o produto das funções h(x) = (3x + 6) e w(x) = (2x – 1) seja negativo?
É possível resolver de várias formas diferentes, dentre elas podemos destacar as seguintes:
• Para que esse produto seja negativo ele deverá ser menor que zero, portanto iremos representá-lo da seguinte forma: (3x + 6) . (2x – 1) < 0. Podemos estudar o sinal de cada uma das funções e em seguida estudar o sinal da inequação, assim serão encontrados os possíveis valores de x que satisfazem a desigualdade.
(3x + 6) . (2x – 1) < 0
h(x) = (3x + 6)
3x + 6 = 0
3x = -6
x = -2
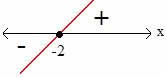
w(x) = (2x – 1)
2x – 1 = 0
2x = 1
x = 1/2
Agora montamos a seguinte tabela que possibilitará encontrar os valores de x:
Portanto, teremos como solução da inequação: S = {x R / -2 < x < 1/2}
• Outra forma de encontrar o valor dessa mesma inequação – produto é transformá-la em uma inequação de 2º grau. Veja como isso acontece:
(3x + 6) . (2x – 1) < 0
6x2 – 3x + 12x – 6 < 0
6x2 + 9x – 6 < 0 → inequação do segundo grau.
Igualamos a expressão algébrica a zero e encontramos os possíveis valores de x:
6x2 + 9x – 6 = 0
Δ = 25
x’ = 1/2
x’’ = -2
Com esses valores estudamos o sinal da inequação, dessa forma encontramos a solução da inequação – produto.
S = {x R / -2 < x < 1/2}
mundoeducacao
- Inequação Produto
Algumas inequações apresentam, no 1º membro, produto de funções que para obter a resolução dessas inequações é preciso fazer o estudo do sinal de todas as funções, a solução seria a intersecção do estudo dos sinais das funções que pertencem...
- Inequação Produto
Algumas inequações apresentam, no 1º membro, produto de funções que para obter a resolução dessas inequações é preciso fazer o estudo do sinal de todas as funções, a solução seria a intersecção do estudo dos sinais das funções que pertencem...
- Inequação De 2º Grau
Inequação do 2º grau na variável x é uma expressão matemática de desigualdade escrita nas seguintes formas redutíveis: ax² + bx + c > 0 ax² + bx + c < 0 ax² + bx + c ≥ 0 ax² + bx + c ≤ 0 onde a, b e c pertencem ao conjunto dos números...
- Inequação Do 1º Grau
Uma inequação do 1° grau na incógnita x é qualquer expressão do 1° grau que pode ser escrita numa das seguintes formas: ax + b > 0; ax + b < 0; ax + b ≥ 0; ax + b ≤ 0. Onde a, b são números reais com a ≠ 0. Exemplos: -2x + 7 >...
- Inequação Do 2º Grau
Uma inequação do 2° grau na incógnita x é uma expressão do 2° grau que pode ser escrita numa das seguintes formas: ax² + bx + c > 0; ax² + bx + c < 0; ax² + bx + c ≥ 0; ax² + bx + c ≤ 0. Para resolvermos uma inequação do Segundo...
Matemática
Inequação – produto
Inequação é uma desigualdade de elementos, portanto uma inequação - produto pode ser representada da seguinte forma:
h(x) . w(x) > 0
h(x) . w(x) < 0
h(x) . w(x) ≠ 0
h(x) . w(x) ≥ 0
h(x) . w(x) ≤ 0
Sendo que h e w estão representando qualquer função (elemento). Por exemplo:
Qual seriam os possíveis valores de x para que o produto das funções h(x) = (3x + 6) e w(x) = (2x – 1) seja negativo?
É possível resolver de várias formas diferentes, dentre elas podemos destacar as seguintes:
• Para que esse produto seja negativo ele deverá ser menor que zero, portanto iremos representá-lo da seguinte forma: (3x + 6) . (2x – 1) < 0. Podemos estudar o sinal de cada uma das funções e em seguida estudar o sinal da inequação, assim serão encontrados os possíveis valores de x que satisfazem a desigualdade.
(3x + 6) . (2x – 1) < 0
h(x) = (3x + 6)
3x + 6 = 0
3x = -6
x = -2
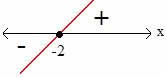
w(x) = (2x – 1)
2x – 1 = 0
2x = 1
x = 1/2
Agora montamos a seguinte tabela que possibilitará encontrar os valores de x:
Portanto, teremos como solução da inequação: S = {x R / -2 < x < 1/2}
• Outra forma de encontrar o valor dessa mesma inequação – produto é transformá-la em uma inequação de 2º grau. Veja como isso acontece:
(3x + 6) . (2x – 1) < 0
6x2 – 3x + 12x – 6 < 0
6x2 + 9x – 6 < 0 → inequação do segundo grau.
Igualamos a expressão algébrica a zero e encontramos os possíveis valores de x:
6x2 + 9x – 6 = 0
Δ = 25
x’ = 1/2
x’’ = -2
Com esses valores estudamos o sinal da inequação, dessa forma encontramos a solução da inequação – produto.
S = {x R / -2 < x < 1/2}
mundoeducacao
- Inequação Produto
Algumas inequações apresentam, no 1º membro, produto de funções que para obter a resolução dessas inequações é preciso fazer o estudo do sinal de todas as funções, a solução seria a intersecção do estudo dos sinais das funções que pertencem...
- Inequação Produto
Algumas inequações apresentam, no 1º membro, produto de funções que para obter a resolução dessas inequações é preciso fazer o estudo do sinal de todas as funções, a solução seria a intersecção do estudo dos sinais das funções que pertencem...
- Inequação De 2º Grau
Inequação do 2º grau na variável x é uma expressão matemática de desigualdade escrita nas seguintes formas redutíveis: ax² + bx + c > 0 ax² + bx + c < 0 ax² + bx + c ≥ 0 ax² + bx + c ≤ 0 onde a, b e c pertencem ao conjunto dos números...
- Inequação Do 1º Grau
Uma inequação do 1° grau na incógnita x é qualquer expressão do 1° grau que pode ser escrita numa das seguintes formas: ax + b > 0; ax + b < 0; ax + b ≥ 0; ax + b ≤ 0. Onde a, b são números reais com a ≠ 0. Exemplos: -2x + 7 >...
- Inequação Do 2º Grau
Uma inequação do 2° grau na incógnita x é uma expressão do 2° grau que pode ser escrita numa das seguintes formas: ax² + bx + c > 0; ax² + bx + c < 0; ax² + bx + c ≥ 0; ax² + bx + c ≤ 0. Para resolvermos uma inequação do Segundo...
