Matemática
Uma forma de encontrar a posição relativa entre uma reta e uma circunferência é verificando a sua intersecção, ou seja, analisando se a reta e a circunferência terão dois pontos em comum, apenas um ponto em comum ou nenhum ponto em comum.
O valor dessa intersecção é a solução do sistema formado com a equação geral da reta e com a equação reduzida da circunferência. Considerando a equação geral da reta ax+by+c = 0 e a equação reduzida da circunferência (x - a)2 + (y - b)2 = R2.
Resolvendo o sistema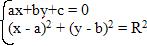 é possível encontrar uma equação do segundo grau, analisando o seu descriminante Δ é possível determinar a posição da reta em relação à circunferência:
é possível encontrar uma equação do segundo grau, analisando o seu descriminante Δ é possível determinar a posição da reta em relação à circunferência:
Δ > 0 reta secante à circunferência
Δ = 0 reta tangente à circunferência
Δ < 0 reta externa à circunferência.
Se o discriminante Δ for maior ou igual à zero, para descobrir as coordenadas dos pontos é preciso terminar a resolução da equação do segundo grau.
Exemplo: Verifique se a circunferência (x+1)2 + y2 = 25 e a reta x + y – 6 = 0 possui algum ponto de intersecção.
Resolução:
x + y – 6 = 0 → equação 1
(x+1)2 + y2 = 25 → equação 2
Escolhemos uma das duas equações e isolamos uma das incógnitas.
x + y – 6 = 0
x = 6 – y
Substituímos o valor de x na equação 2.
(6 – y +1)2 + y2 = 25
(-y + 7)2 + y2 = 25
(-y)2 – 14y + 49 + y2 = 25
y2 – 14y + 49 – 25 + y2 = 0
2y2 – 14y + 24 = 0 (: 2)
y2 – 7y + 12 = 0
Δ = b2 – 4ac
Δ = (-7)2 – 4 . 1 . 12
Δ = 49 – 48
Δ = 1
Como o descriminante Δ é maior que zero sabemos que essa reta é secante à circunferência, agora para descobrir o valor das coordenadas dos dois pontos pertencentes à circunferência é preciso terminar de resolver a equação.
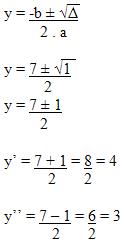
Para y’= 4
x = 6 – y
x = 6 – 4
x = 2
Para y’’ = 3
x = 6 – y
x = 6 – 3
x = 3
Portanto, os dois pontos que interceptam a circunferência são: (2,4) e (3,3).
www.mundoeducacao.com.br
- Circunferências
Verifique qual a posição dos pontos P(0,0); Q(1,-4); R(-2,-5) em relação à circunferência de equação x2 + y2 + 2x + 8y + 13 = 0 Deve-se transformar essa equação normal em reduzida. x2 + y2 + 2x + 8y + 13 = 0 x2 + 2x + y2 + 8y = -13 (x2 + 2x...
- Equação Reduzida Da Circunferência
Da mesma forma que equacionamos uma reta é possível também representarmos uma circunferência na forma de equações, utilizando seu centro e um ponto genérico da circunferência. Veja a representação em um plano cartesiano de uma circunferência...
- Equação Reduzida Da Circunferência
Equação reduzida da circunferênciaMarcelo Rigonatto CircunferênciaDo ponto de vista analítico, circunferência é o conjunto dos pontos P(x, y) do plano que equidistam (apresentam a mesma distância) de um ponto O. Essa distância...
- Equação Da Circunferência
Da mesma forma que equacionamos uma reta é possível também representarmos uma circunferência na forma de equações, utilizando seu centro e um ponto genérico da circunferência. Veja a representação em um plano cartesiano de uma circunferência...
- Circunferências
CIRCUNFERÊNCIA É o conjunto dos pontos do plano cuja distância ao ponto C é igual a r. O ponto C é chamado centro da circunferência e o segmento de reta que liga um ponto qualquer dela ao centro é chamado raio da circunferência. Assim, r é a...
Matemática
Interseção de reta e circunferências
Uma forma de encontrar a posição relativa entre uma reta e uma circunferência é verificando a sua intersecção, ou seja, analisando se a reta e a circunferência terão dois pontos em comum, apenas um ponto em comum ou nenhum ponto em comum.
O valor dessa intersecção é a solução do sistema formado com a equação geral da reta e com a equação reduzida da circunferência. Considerando a equação geral da reta ax+by+c = 0 e a equação reduzida da circunferência (x - a)2 + (y - b)2 = R2.
Resolvendo o sistema
Δ > 0 reta secante à circunferência
Δ = 0 reta tangente à circunferência
Δ < 0 reta externa à circunferência.
Se o discriminante Δ for maior ou igual à zero, para descobrir as coordenadas dos pontos é preciso terminar a resolução da equação do segundo grau.
Exemplo: Verifique se a circunferência (x+1)2 + y2 = 25 e a reta x + y – 6 = 0 possui algum ponto de intersecção.
Resolução:
x + y – 6 = 0 → equação 1
(x+1)2 + y2 = 25 → equação 2
Escolhemos uma das duas equações e isolamos uma das incógnitas.
x + y – 6 = 0
x = 6 – y
Substituímos o valor de x na equação 2.
(6 – y +1)2 + y2 = 25
(-y + 7)2 + y2 = 25
(-y)2 – 14y + 49 + y2 = 25
y2 – 14y + 49 – 25 + y2 = 0
2y2 – 14y + 24 = 0 (: 2)
y2 – 7y + 12 = 0
Δ = b2 – 4ac
Δ = (-7)2 – 4 . 1 . 12
Δ = 49 – 48
Δ = 1
Como o descriminante Δ é maior que zero sabemos que essa reta é secante à circunferência, agora para descobrir o valor das coordenadas dos dois pontos pertencentes à circunferência é preciso terminar de resolver a equação.
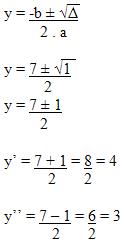
Para y’= 4
x = 6 – y
x = 6 – 4
x = 2
Para y’’ = 3
x = 6 – y
x = 6 – 3
x = 3
Portanto, os dois pontos que interceptam a circunferência são: (2,4) e (3,3).
www.mundoeducacao.com.br
- Circunferências
Verifique qual a posição dos pontos P(0,0); Q(1,-4); R(-2,-5) em relação à circunferência de equação x2 + y2 + 2x + 8y + 13 = 0 Deve-se transformar essa equação normal em reduzida. x2 + y2 + 2x + 8y + 13 = 0 x2 + 2x + y2 + 8y = -13 (x2 + 2x...
- Equação Reduzida Da Circunferência
Da mesma forma que equacionamos uma reta é possível também representarmos uma circunferência na forma de equações, utilizando seu centro e um ponto genérico da circunferência. Veja a representação em um plano cartesiano de uma circunferência...
- Equação Reduzida Da Circunferência
Equação reduzida da circunferênciaMarcelo Rigonatto CircunferênciaDo ponto de vista analítico, circunferência é o conjunto dos pontos P(x, y) do plano que equidistam (apresentam a mesma distância) de um ponto O. Essa distância...
- Equação Da Circunferência
Da mesma forma que equacionamos uma reta é possível também representarmos uma circunferência na forma de equações, utilizando seu centro e um ponto genérico da circunferência. Veja a representação em um plano cartesiano de uma circunferência...
- Circunferências
CIRCUNFERÊNCIA É o conjunto dos pontos do plano cuja distância ao ponto C é igual a r. O ponto C é chamado centro da circunferência e o segmento de reta que liga um ponto qualquer dela ao centro é chamado raio da circunferência. Assim, r é a...
