Matemática
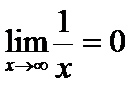
A noção de limite é basicamente intuitiva, pois estamos estudando a relação entre o domínio e a imagem de uma função, atribuindo valores a x e verificando os valores próximos da imagem, por isso dizemos que o número tende a um valor específico.
Vamos analisar o limite da função f(x) = 2x + 4, quando o domínio tende aos números 0, 1, 2, 3, 4 e 5.
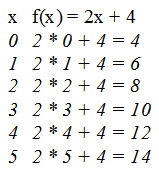
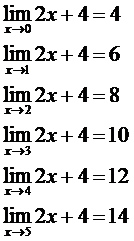
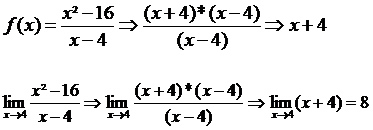
- Função
Pra que uma função seja considerada do 2º grau, ela terá que assumir certas características, como: Toda função do 2º grau deve ser dos reais para os reais, definida pela fórmula f(x) = ax2 + bx + c, sendo que a deve pertencer ao conjunto dos...
- Função 2º Grau
Uma função para ser do 2º grau precisa assumir algumas características, pois ela deve ser dos reais para os reais, definida pela fórmula f(x) = ax2 + bx + c, sendo que a, b e c são números reais com a diferente de zero. Concluímos que a condição...
- Função Exponencial
Função exponencial é uma função na qual a variável (incógnita) se encontra no expoente. A função exponencial pode ser escrita de forma geral, veja como: f : R → R*+ tal que f(x) = ax, sendo que a R*+ e a ≠ 1. Essa representação significa:...
- Limites
Consideremos a função real, de variável real, definida por . Observando o gráfico da função, que esboçámos ao lado, conclui-se que: Não existe . ...
- Função Do 1º Grau
Uma função do 1º grau pode ser chamada de função afim. Pra que uma função seja considerada afim ela terá que assumir certas características, como: Toda função do 1º grau deve ser dos reais para os reais, definida pela fórmula f(x) = ax +...
Matemática
Limite
O Limite tem por objetivo estudar uma função à medida que o seu domínio se aproxima de determinado valor, dessa forma, analisamos o valor da imagem de acordo com o domínio. Por exemplo, a função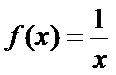 
tende a zero quando o domínio caminha sentido ao infinito. Veja tabela:
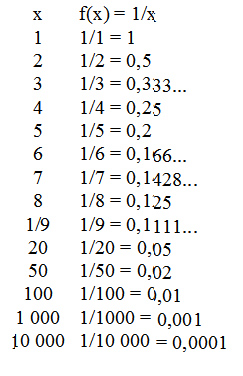
Note que à medida que o valor de x aumenta, o respectivo valor de y diminui, aproximando-se de zero.
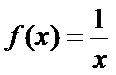tende a zero quando o domínio caminha sentido ao infinito. Veja tabela: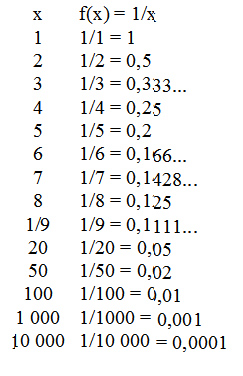Note que à medida que o valor de x aumenta, o respectivo valor de y diminui, aproximando-se de zero.
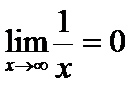
A noção de limite é basicamente intuitiva, pois estamos estudando a relação entre o domínio e a imagem de uma função, atribuindo valores a x e verificando os valores próximos da imagem, por isso dizemos que o número tende a um valor específico.
Vamos analisar o limite da função f(x) = 2x + 4, quando o domínio tende aos números 0, 1, 2, 3, 4 e 5.
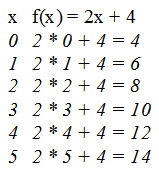
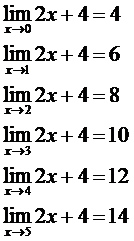
Em algumas situações, a determinação de limites envolve a simplificação da função. Por exemplo, vamos determinar o limite da função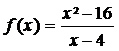 
quando o valor de x tende a 4.
Nessa função, o denominador possui uma restrição quanto ao valor de x = 4, então precisamos trabalhar a função de forma que ela aceite o valor de x. Observe:
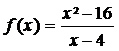quando o valor de x tende a 4.Nessa função, o denominador possui uma restrição quanto ao valor de x = 4, então precisamos trabalhar a função de forma que ela aceite o valor de x. Observe:
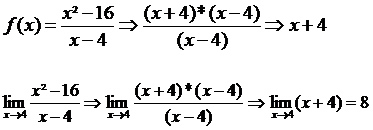
mundoeducacao
- Função
Pra que uma função seja considerada do 2º grau, ela terá que assumir certas características, como: Toda função do 2º grau deve ser dos reais para os reais, definida pela fórmula f(x) = ax2 + bx + c, sendo que a deve pertencer ao conjunto dos...
- Função 2º Grau
Uma função para ser do 2º grau precisa assumir algumas características, pois ela deve ser dos reais para os reais, definida pela fórmula f(x) = ax2 + bx + c, sendo que a, b e c são números reais com a diferente de zero. Concluímos que a condição...
- Função Exponencial
Função exponencial é uma função na qual a variável (incógnita) se encontra no expoente. A função exponencial pode ser escrita de forma geral, veja como: f : R → R*+ tal que f(x) = ax, sendo que a R*+ e a ≠ 1. Essa representação significa:...
- Limites
Consideremos a função real, de variável real, definida por . Observando o gráfico da função, que esboçámos ao lado, conclui-se que: Não existe . ...
- Função Do 1º Grau
Uma função do 1º grau pode ser chamada de função afim. Pra que uma função seja considerada afim ela terá que assumir certas características, como: Toda função do 1º grau deve ser dos reais para os reais, definida pela fórmula f(x) = ax +...