Matemática
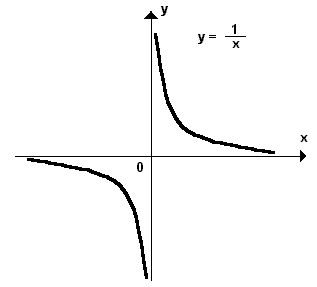
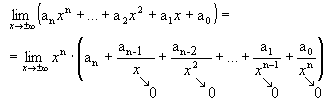
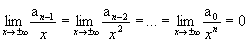
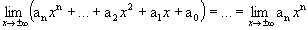
- ...::definição De Função Do 1º Grau E Zero De Uma Função Do 1º Grau::...
FUNÇÃO DO 1º GRAU Prof. Esp. Deivison da Silva e Silvae-mail:[email protected]...
- Fatoração
Professor de Matemática no Colégio Estadual Dinah GonçalvesE Biologia na rede privada de Salvador-BahiaProfessor Antonio Carlos carneiro Barrosoemail [email protected] HTTP://ensinodematemtica.blogspot.com eHTTP://accbarroso60.wordpress.com...
- Limite De Uma Função
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...
- Limite
O Limite tem por objetivo estudar uma função à medida que o seu domínio se aproxima de determinado valor, dessa forma, analisamos o valor da imagem de acordo com o domínio. Por exemplo, a função tende a zero quando o domínio caminha sentido ao...
- Limites
Consideremos a função real, de variável real, definida por . Observando o gráfico da função, que esboçámos ao lado, conclui-se que: Não existe . ...
Matemática
Limites
Limites envolvendo infinito
Conforme sabemos, a expressão x 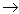
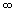 (xtende para infinito) significa que x assume valores superiores a qualquer número real e x
(xtende para infinito) significa que x assume valores superiores a qualquer número real e x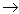
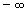 (xtende para menos infinitos), da mesma forma, indica que xassume valores menores que qualquer número real.
(xtende para menos infinitos), da mesma forma, indica que xassume valores menores que qualquer número real.
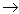
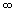 (xtende para infinito) significa que x assume valores superiores a qualquer número real e x
(xtende para infinito) significa que x assume valores superiores a qualquer número real e x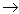
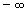 (xtende para menos infinitos), da mesma forma, indica que xassume valores menores que qualquer número real.
(xtende para menos infinitos), da mesma forma, indica que xassume valores menores que qualquer número real. Exemplo:
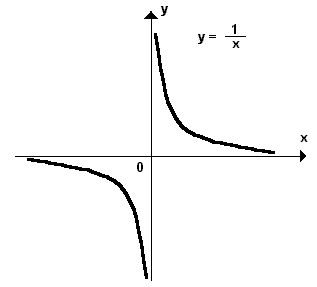
a) 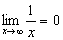 , ou seja, à medida que xaumenta, ytende para zero e o limite é zero.
, ou seja, à medida que xaumenta, ytende para zero e o limite é zero.
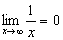 , ou seja, à medida que xaumenta, ytende para zero e o limite é zero.
, ou seja, à medida que xaumenta, ytende para zero e o limite é zero.b) 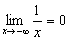 , ou seja, à medida que x diminui, y tende para zero e o limite é zero.
, ou seja, à medida que x diminui, y tende para zero e o limite é zero.
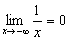 , ou seja, à medida que x diminui, y tende para zero e o limite é zero.
, ou seja, à medida que x diminui, y tende para zero e o limite é zero. c) 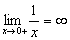 , ou seja, quando x se aproxima de zero pela direita de zero
, ou seja, quando x se aproxima de zero pela direita de zero 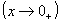 ou por valores maiores que zero, y tende para o infinito e o limite é infinito.
ou por valores maiores que zero, y tende para o infinito e o limite é infinito.
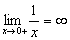 , ou seja, quando x se aproxima de zero pela direita de zero
, ou seja, quando x se aproxima de zero pela direita de zero 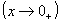 ou por valores maiores que zero, y tende para o infinito e o limite é infinito.
ou por valores maiores que zero, y tende para o infinito e o limite é infinito.d) 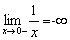 , ou seja, quando x tende para zero pela esquerda ou por valores menores que zero, ytende para menos infinito
, ou seja, quando x tende para zero pela esquerda ou por valores menores que zero, ytende para menos infinito
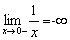 , ou seja, quando x tende para zero pela esquerda ou por valores menores que zero, ytende para menos infinito
, ou seja, quando x tende para zero pela esquerda ou por valores menores que zero, ytende para menos infinitoLimite de uma função polinomial para 

Seja a função polinomial 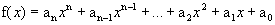 . Então:
. Então:
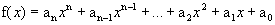 . Então:
. Então: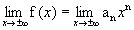 |
Demonstração:
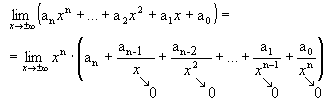
Mas:
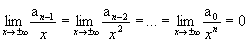
Logo:
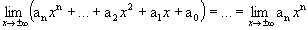
De forma análoga, para 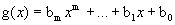 , temos:
, temos:
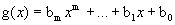 , temos:
, temos: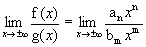 |
Exemplos:
Fonte:http://www.somatematica.com.br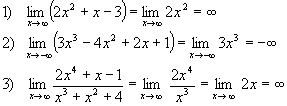
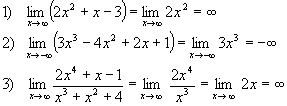
- ...::definição De Função Do 1º Grau E Zero De Uma Função Do 1º Grau::...
FUNÇÃO DO 1º GRAU Prof. Esp. Deivison da Silva e Silvae-mail:[email protected]...
- Fatoração
Professor de Matemática no Colégio Estadual Dinah GonçalvesE Biologia na rede privada de Salvador-BahiaProfessor Antonio Carlos carneiro Barrosoemail [email protected] HTTP://ensinodematemtica.blogspot.com eHTTP://accbarroso60.wordpress.com...
- Limite De Uma Função
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...
- Limite
O Limite tem por objetivo estudar uma função à medida que o seu domínio se aproxima de determinado valor, dessa forma, analisamos o valor da imagem de acordo com o domínio. Por exemplo, a função tende a zero quando o domínio caminha sentido ao...
- Limites
Consideremos a função real, de variável real, definida por . Observando o gráfico da função, que esboçámos ao lado, conclui-se que: Não existe . ...
