Matemática
Para compreender melhor o que é uma matriz, iremos compará-la com uma tabela. Toda tabela é formada por linhas e colunas, assim como uma matriz. Na matriz indicamos a quantidade de linhas por m e a quantidade de colunas por n. Tanto em uma tabela como em uma matriz a quantidade de linhas e colunas deve ser maior ou igual a um e somente números naturais.
Matematicamente podemos definir matriz como:
Uma matriz m x n com m N* e n
N* e n  N* será disposta em m linhas e n colunas.
N* será disposta em m linhas e n colunas.
A representação de matrizes é feita de três formas diferentes:
Os elementos são colocados entre parênteses:
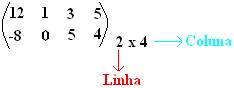
Os elementos são colocados entre colchetes:
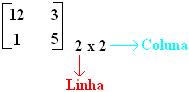
Os elementos são colocados entre duas barras paralelas:

Observado as matrizes acima percebemos que todas são compostas por números e esses são os elementos das matrizes. Todos os elementos pertencem a uma determinada linha e coluna de uma matriz.
Dada a matriz qualquer A3x2 (lê-se matriz A de ordem dois por três), veja como é feita a sua representação.

O elemento a11 pertence a 3° linha e 2° coluna.
O elemento a21 pertence a 2º linha e 3° coluna.
O elemento a31 pertence a 3° linha e 1° coluna.
O elemento a12 pertence a 1º linha e 2° coluna.
O elemento a22 pertence a 2º linha e 2º coluna.
O elemento a32 pertence a 3º linha e 2º coluna.
Podemos dizer que aij i representa a linha e j representa a coluna.
Veja o exemplo abaixo:
Escreva a matriz B = (bij)2x3 que bij = i . j.
Devemos construir uma matriz B com duas linhas e três colunas:

Cada elemento deverá obedecer a seguinte regra bij = i . j.
b11 = 1 . 1
b11 = 1
b21 = 2 . 1
b21 = 2
b12 = 1 .2
b12 = 2
b22 = 2 . 2
b22 = 4
b13 = 1 . 3
b13 = 3
b23 = 2 . 3
b23 = 6
Colocando cada valor em seu determinado elemento na matriz b, podemos concluir que a matriz B será determinada pelos seguintes elementos:
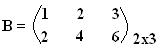
www.mundoeducacao.com.br
- Adição E Subtração De Matrizes
Matriz é um conjunto de elementos organizados em linhas e colunas. Cada elemento da matriz ocupa um lugar numa linha e numa coluna e sua representação informa onde ele está localizado na matriz. Por exemplo, numa matriz A de ordem 3 x 3 (com três...
- Determinantes
Se A é uma matriz quadrada A de ordem 2, dada por: a11 a12 a21 a22 definimos o determinante desta matriz A, denotado por det(A), como: det(A) = a11.a22 - a21.a12 Se A é uma matriz quadrada A de ordem 3, dada por: a11 a12 a13 a21 a22 a23 a31 a32 a33...
- Determinantes
Se A é uma matriz quadrada A de ordem 2, dada por: a11 a12 a21 a22 definimos o determinante desta matriz A, denotado por det(A), como: det(A) = a11.a22 - a21.a12 Se A é uma matriz quadrada A de ordem 3, dada por: a11 a12 a13 a21 a22 a23 a31 a32 a33...
- Adição E Subtração De Matrizes
Matriz é um conjunto de elementos organizados em linhas e colunas. Cada elemento da matriz ocupa um lugar numa linha e numa coluna e sua representação informa onde ele está localizado na matriz. Por exemplo, numa matriz A de ordem 3 x 3 (com três...
- Menor Complementar
Menor complementar de um elemento de uma matriz é o determinante dela, eliminando a linha e a coluna que pertencer esse elemento. É possível calcular o menor complementar se a matriz for quadrada e de ordem maior ou igual a 2. Dada uma matriz de ordem...
Matemática
Matriz
Para compreender melhor o que é uma matriz, iremos compará-la com uma tabela. Toda tabela é formada por linhas e colunas, assim como uma matriz. Na matriz indicamos a quantidade de linhas por m e a quantidade de colunas por n. Tanto em uma tabela como em uma matriz a quantidade de linhas e colunas deve ser maior ou igual a um e somente números naturais.
Matematicamente podemos definir matriz como:
Uma matriz m x n com m
 N* e n
N* e n  N* será disposta em m linhas e n colunas.
N* será disposta em m linhas e n colunas.A representação de matrizes é feita de três formas diferentes:
Os elementos são colocados entre parênteses:
Os elementos são colocados entre colchetes:
Os elementos são colocados entre duas barras paralelas:
Observado as matrizes acima percebemos que todas são compostas por números e esses são os elementos das matrizes. Todos os elementos pertencem a uma determinada linha e coluna de uma matriz.
Dada a matriz qualquer A3x2 (lê-se matriz A de ordem dois por três), veja como é feita a sua representação.
O elemento a11 pertence a 3° linha e 2° coluna.
O elemento a21 pertence a 2º linha e 3° coluna.
O elemento a31 pertence a 3° linha e 1° coluna.
O elemento a12 pertence a 1º linha e 2° coluna.
O elemento a22 pertence a 2º linha e 2º coluna.
O elemento a32 pertence a 3º linha e 2º coluna.
Podemos dizer que aij i representa a linha e j representa a coluna.
Veja o exemplo abaixo:
Escreva a matriz B = (bij)2x3 que bij = i . j.
Devemos construir uma matriz B com duas linhas e três colunas:
Cada elemento deverá obedecer a seguinte regra bij = i . j.
b11 = 1 . 1
b11 = 1
b21 = 2 . 1
b21 = 2
b12 = 1 .2
b12 = 2
b22 = 2 . 2
b22 = 4
b13 = 1 . 3
b13 = 3
b23 = 2 . 3
b23 = 6
Colocando cada valor em seu determinado elemento na matriz b, podemos concluir que a matriz B será determinada pelos seguintes elementos:
www.mundoeducacao.com.br
- Adição E Subtração De Matrizes
Matriz é um conjunto de elementos organizados em linhas e colunas. Cada elemento da matriz ocupa um lugar numa linha e numa coluna e sua representação informa onde ele está localizado na matriz. Por exemplo, numa matriz A de ordem 3 x 3 (com três...
- Determinantes
Se A é uma matriz quadrada A de ordem 2, dada por: a11 a12 a21 a22 definimos o determinante desta matriz A, denotado por det(A), como: det(A) = a11.a22 - a21.a12 Se A é uma matriz quadrada A de ordem 3, dada por: a11 a12 a13 a21 a22 a23 a31 a32 a33...
- Determinantes
Se A é uma matriz quadrada A de ordem 2, dada por: a11 a12 a21 a22 definimos o determinante desta matriz A, denotado por det(A), como: det(A) = a11.a22 - a21.a12 Se A é uma matriz quadrada A de ordem 3, dada por: a11 a12 a13 a21 a22 a23 a31 a32 a33...
- Adição E Subtração De Matrizes
Matriz é um conjunto de elementos organizados em linhas e colunas. Cada elemento da matriz ocupa um lugar numa linha e numa coluna e sua representação informa onde ele está localizado na matriz. Por exemplo, numa matriz A de ordem 3 x 3 (com três...
- Menor Complementar
Menor complementar de um elemento de uma matriz é o determinante dela, eliminando a linha e a coluna que pertencer esse elemento. É possível calcular o menor complementar se a matriz for quadrada e de ordem maior ou igual a 2. Dada uma matriz de ordem...
