Matemática
Matriz triangular inferior
Matriz em que os elementos acima da diagonal são iguais a zero.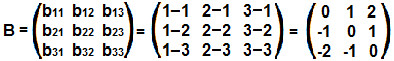
Esse modelo de matriz demonstra uma característica especial somente nas matrizes triangulares. Nelas, o produto dos elementos da diagonal principal é igual ao determinante da matriz, calculado de acordo com a regra de Sarrus. Veja:
Dada a matriz triangular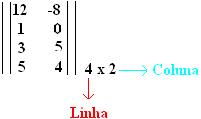
, calcularemos o seu determinante aplicando Sarrus e, logo na sequência, verificar se o valor do determinante corresponde à multiplicação dos elementos da diagonal principal da matriz triangular.
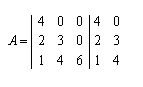
Aplicando Sarrus
Diagonal principal
4 * 3 * 6 = 72
0 * 0 * 1 = 0
0 * 2 * 4 = 0
72 + 0 + 0 = 72
Diagonal secundária
0 * 2 * 6 = 0
4 * 0 * 4 = 0
0 * 3 * 1 = 0
–16 + 0 + 0 = –16
Determinante de A72 + 0
72
Multiplicando os elementos da diagonal principal
4 * 3 * 6 = 72
Observe que os resultados são os mesmos, portanto, a regra para o cálculo do determinante nas matrizes triangulares é válida.
- Área Da Região Triangular Em Relação As Coordenadas Dos Vértices
Podemos determinar a área de uma região triangular utilizando expressões relacionadas à Geometria Plana. Nas situações envolvendo coordenadas de posicionamento dos vértices de um triângulo, os cálculos são efetuados de acordo com o determinante...
- Matriz Quadrada
Matriz quadrada é um tipo especial de matriz que possui o mesmo número de linhas e o mesmo de colunas. Ou seja, dada uma matriz A n x m será uma matriz quadrada se, somente se, n = m. Por exemplo: B = (5) 1x1 A matriz B possui apenas um elemento e...
- Determinante De Uma Matriz Quadrada De Ordem N
Para conhecermos o determinante de uma matriz de ordem 2x2 e 3x3 utilizamos a Regra de Sarrus. Nos casos em que a ordem for maior que 3x3 devemos utilizar o Teorema de Laplace. Enfatizaremos nosso estudo dos determinantes nas matrizes de ordem 2x2 e 3x3...
- Propriedades Dos Determinantes
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com As propriedades...
- Regra De Sarrus
Regra de SarrusMarcos Noé Regra de SarrusA Regra de Sarrus é utilizada no cálculo de determinantes de matrizes quadradas. Sua aplicação permite o cálculo de maneira prática, relacionando a diagonal principal com a diagonal...
Matemática
Matriz Triangular
Uma matriz constitui uma ferramenta matemática utilizada em diversas situações relacionadas à Informática e Engenharia. Elas são formadas por elementos distribuídos em linhas e colunas (aij), onde i: linhas e j: colunas. As matrizes possuem inúmeras situações especiais, como matriz coluna, matriz quadrada, matriz nula, matriz identidade, matriz diagonal e matriz triangular.
Vamos abordar as características de uma matriz triangular, classificada em superior ou inferior. Observe:
Matriz triangular superior
Matriz em que os elementos abaixo da diagonal principal são iguais a zero.
Vamos abordar as características de uma matriz triangular, classificada em superior ou inferior. Observe:
Matriz triangular superior
Matriz em que os elementos abaixo da diagonal principal são iguais a zero.
Matriz triangular inferior
Matriz em que os elementos acima da diagonal são iguais a zero.
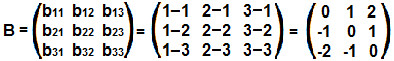
Dada a matriz triangular
, calcularemos o seu determinante aplicando Sarrus e, logo na sequência, verificar se o valor do determinante corresponde à multiplicação dos elementos da diagonal principal da matriz triangular.Aplicando Sarrus
Diagonal principal
4 * 3 * 6 = 72
0 * 0 * 1 = 0
0 * 2 * 4 = 0
72 + 0 + 0 = 72
Diagonal secundária
0 * 2 * 6 = 0
4 * 0 * 4 = 0
0 * 3 * 1 = 0
–16 + 0 + 0 = –16
Determinante de A72 + 0
72
Multiplicando os elementos da diagonal principal
4 * 3 * 6 = 72
Observe que os resultados são os mesmos, portanto, a regra para o cálculo do determinante nas matrizes triangulares é válida.
- Área Da Região Triangular Em Relação As Coordenadas Dos Vértices
Podemos determinar a área de uma região triangular utilizando expressões relacionadas à Geometria Plana. Nas situações envolvendo coordenadas de posicionamento dos vértices de um triângulo, os cálculos são efetuados de acordo com o determinante...
- Matriz Quadrada
Matriz quadrada é um tipo especial de matriz que possui o mesmo número de linhas e o mesmo de colunas. Ou seja, dada uma matriz A n x m será uma matriz quadrada se, somente se, n = m. Por exemplo: B = (5) 1x1 A matriz B possui apenas um elemento e...
- Determinante De Uma Matriz Quadrada De Ordem N
Para conhecermos o determinante de uma matriz de ordem 2x2 e 3x3 utilizamos a Regra de Sarrus. Nos casos em que a ordem for maior que 3x3 devemos utilizar o Teorema de Laplace. Enfatizaremos nosso estudo dos determinantes nas matrizes de ordem 2x2 e 3x3...
- Propriedades Dos Determinantes
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com As propriedades...
- Regra De Sarrus
Regra de SarrusMarcos Noé Regra de SarrusA Regra de Sarrus é utilizada no cálculo de determinantes de matrizes quadradas. Sua aplicação permite o cálculo de maneira prática, relacionando a diagonal principal com a diagonal...