Matemática
- Questão 79 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
Observe os dados numéricos ordenados obtidos em uma pesquisa: 23, 24, 28, x, y, 37, 40, 48 (x e y representam números inteiros). Sobre esses dados, sabe-se que a moda é 28, e que a mediana é 30. É possível concluir que (A) x =...
- Questão 8 ? Professor De Matemática ? Seap ? Paraná ? 2.013
A seqüência 4, 7, 8, 6, 7, 9, 5, 10, 8, 6, 7 indica as notas de Estatística dos 11 alunos que estão cursando uma Pós-Graduação em Matemática. Assinale a alternativa que apresenta os valores da moda, mediana e variância desses dados, nessa ordem....
- Questão 79 ? Prova Do Estado ? (ofa) 2.013 ? Professor De Educação Básica Ii
Com relação às notas de Matemática do 2.º bimestre de uma determinada turma, tem-se as seguintes informações: (1) elas variaram de 0,0 a 10,0; (2) a média dessas notas é 7,0; (3) a mediana dessas notas é 7,75; (4) 8,0 é a nota que mais vezes...
- Moda E Mediana
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...
- Moda E Mediana
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com...
Matemática
Moda e mediana
Ao realizar uma pesquisa é aconselhável realizar um estudo estatístico dos dados apresentados. Através desse estudo podemos tirar as conclusões necessárias sobre o universo pesquisado. A estatística descritiva é a parte da estatística responsável por realizar essa análise, apontando tendências de comportamento das variáveis, criando gráficos e descrevendo as características dos conjuntos pesquisados.
Numa pesquisa, os dados tendem a se concentrar em torno dos valores centrais. Esses valores centrais são chamados de medidas de tendência central. São elas: Média, Moda e Mediana. Iremos abordar e conceituar Moda e Mediana.
Definição de Moda (Mo): é o valor que mais aparece num conjunto de dados.
Exemplo 1. Os dados abaixo se referem à idade de 20 alunos de uma turma de 6º ano.
Idade: {12, 11, 12, 13, 12, 11, 13, 12, 12, 11, 14, 13, 13, 12, 11, 12, 13, 14, 11, 14}
A moda desse conjunto de dados será a idade que mais aparece, ou seja:
Mo = 12 (pois é a idade que aparece mais vezes no conjunto)
Exemplo 2. A tabela abaixo apresenta as notas em matemática de uma turma de 30 alunos.

Numa pesquisa, os dados tendem a se concentrar em torno dos valores centrais. Esses valores centrais são chamados de medidas de tendência central. São elas: Média, Moda e Mediana. Iremos abordar e conceituar Moda e Mediana.
Definição de Moda (Mo): é o valor que mais aparece num conjunto de dados.
Exemplo 1. Os dados abaixo se referem à idade de 20 alunos de uma turma de 6º ano.
Idade: {12, 11, 12, 13, 12, 11, 13, 12, 12, 11, 14, 13, 13, 12, 11, 12, 13, 14, 11, 14}
A moda desse conjunto de dados será a idade que mais aparece, ou seja:
Mo = 12 (pois é a idade que aparece mais vezes no conjunto)
Exemplo 2. A tabela abaixo apresenta as notas em matemática de uma turma de 30 alunos.

Na coluna da esquerda temos as notas na disciplina de matemática e na coluna da direita, quantos alunos obtiveram a respectiva nota. Dessa forma, podemos observar que a nota que mais aparece nesse conjunto de dados é 7. Portanto,
Mo = 7.
Exemplo 3. Os dados abaixo são referentes ao número dos calçados vendidos em uma loja num determinado dia.
{35, 33, 36, 35, 37, 36, 39, 40, 42, 43, 35, 36, 42}
Nesse caso, existem dois números de sapatos que aparecem mais vezes: 35 e 36. Logo, a moda pode ser:
Mo = 35 ou Mo = 36
Quando isso ocorre, dizemos que o conjunto de dados é bimodal.
Definição de Mediana (Md): é o valor (pertencente ou não ao conjunto de dados) que divide o conjunto de dados em dois subconjuntos de mesmo tamanho. De uma forma mais simples, é o valor que divide o conjunto de dados ao meio.
Para determinar a mediana de um conjunto de dados é necessário, primeiro, construir o rol. O rol é a ordenação do conjunto de dados em ordem crescente ou decrescente.
1. Mediana de um conjunto de dados com número de elementos ímpar.
Considere o conjunto de dados abaixo, referentes ao salário médio dos funcionários de uma empresa em reais.
Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980
Observe que nesse conjunto de dados temos 9 elementos, 9 salários. Primeiro devemos montar o rol:
Rol = {1100, 1200, 1210, 1250, 1300, 1450, 1500, 1600, 1980}
Quando o número de elementos do conjunto de dados for ímpar, a mediana é o valor que divide o conjunto ao meio, portanto Md = 1300. Observe que à esquerda e à direita de 1300 existem 4 elementos.
2. Mediana de um conjunto de dados com número de elementos ímpar.
Considere o conjunto de dados abaixo, referente ao salário médio dos funcionários de uma empresa.
Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980 1420
Rol = { 1100, 1200, 1210, 1250, 1300, 1420, 1450, 1500, 1600, 1980}
Nesse conjunto existem 10 elementos. Nesse caso a mediana será a média aritmética dos dois valores centrais. Note que tanto à direita como à esquerda dos dois valores centrais há 4 elementos. Assim,
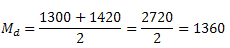
Mo = 7.
Exemplo 3. Os dados abaixo são referentes ao número dos calçados vendidos em uma loja num determinado dia.
{35, 33, 36, 35, 37, 36, 39, 40, 42, 43, 35, 36, 42}
Nesse caso, existem dois números de sapatos que aparecem mais vezes: 35 e 36. Logo, a moda pode ser:
Mo = 35 ou Mo = 36
Quando isso ocorre, dizemos que o conjunto de dados é bimodal.
Definição de Mediana (Md): é o valor (pertencente ou não ao conjunto de dados) que divide o conjunto de dados em dois subconjuntos de mesmo tamanho. De uma forma mais simples, é o valor que divide o conjunto de dados ao meio.
Para determinar a mediana de um conjunto de dados é necessário, primeiro, construir o rol. O rol é a ordenação do conjunto de dados em ordem crescente ou decrescente.
1. Mediana de um conjunto de dados com número de elementos ímpar.
Considere o conjunto de dados abaixo, referentes ao salário médio dos funcionários de uma empresa em reais.
Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980
Observe que nesse conjunto de dados temos 9 elementos, 9 salários. Primeiro devemos montar o rol:
Rol = {1100, 1200, 1210, 1250, 1300, 1450, 1500, 1600, 1980}
Quando o número de elementos do conjunto de dados for ímpar, a mediana é o valor que divide o conjunto ao meio, portanto Md = 1300. Observe que à esquerda e à direita de 1300 existem 4 elementos.
2. Mediana de um conjunto de dados com número de elementos ímpar.
Considere o conjunto de dados abaixo, referente ao salário médio dos funcionários de uma empresa.
Salário: 1500 1300 1200 1250 1600 1100 1450 1210 1980 1420
Rol = { 1100, 1200, 1210, 1250, 1300, 1420, 1450, 1500, 1600, 1980}
Nesse conjunto existem 10 elementos. Nesse caso a mediana será a média aritmética dos dois valores centrais. Note que tanto à direita como à esquerda dos dois valores centrais há 4 elementos. Assim,
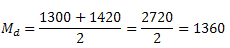
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Especialista em Estatística e Modelagem Matemática
- Questão 79 ? Prova Do Estado ? (ofa) 2.014 ? Professor De Educação Básica Ii
Observe os dados numéricos ordenados obtidos em uma pesquisa: 23, 24, 28, x, y, 37, 40, 48 (x e y representam números inteiros). Sobre esses dados, sabe-se que a moda é 28, e que a mediana é 30. É possível concluir que (A) x =...
- Questão 8 ? Professor De Matemática ? Seap ? Paraná ? 2.013
A seqüência 4, 7, 8, 6, 7, 9, 5, 10, 8, 6, 7 indica as notas de Estatística dos 11 alunos que estão cursando uma Pós-Graduação em Matemática. Assinale a alternativa que apresenta os valores da moda, mediana e variância desses dados, nessa ordem....
- Questão 79 ? Prova Do Estado ? (ofa) 2.013 ? Professor De Educação Básica Ii
Com relação às notas de Matemática do 2.º bimestre de uma determinada turma, tem-se as seguintes informações: (1) elas variaram de 0,0 a 10,0; (2) a média dessas notas é 7,0; (3) a mediana dessas notas é 7,75; (4) 8,0 é a nota que mais vezes...
- Moda E Mediana
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...
- Moda E Mediana
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com...
