Noções Fundamentais da Geometria. Idéias de ponto, reta e plano.
Matemática

Noções Fundamentais da Geometria. Idéias de ponto, reta e plano.



Ponto, Reta e Plano: Noções fundamentais da Geometria
by Roberto M.
O que é ponto? O que é reta? O que é plano? 
A Geometria tem seu início com as noções (idéias) de ponto, de reta e de plano.
Primeiramente, vou dizer que não existe definição para ponto,reta e plano.
Eles são conceitos que apreendemos através de nossas observações e experiências. Com nossos sentidos, formamos idéias, temos impressão, imaginamos o significado de ponto, reta e plano.
Vamos então imaginar: 

Ponto

- O ponto não tem tamanho;
- O ponto não tem dimensão;
- O simples toque do lápis no papel nos dá a idéia de um ponto;
- Uma estrela no céu, ou uma picada de agulha na pele são outras sensações de ponto;
- Por não ter tamanho, ele está em qualquer lugar, sendo assim, tudo é formado por pontos, toda e qualquer figura geométrica é formada por infinitos pontos. As figuras geométricas são formadas por um conjunto de pontos.
- Geralmente, para se indicar os pontos, usam-se as letras maiúsculas do nosso alfabeto: A, B, C, D, E, O, P, Q, etc.
- É fácil representar as imagens de pontos. Pegando um lápis e uma folha de papel, é só encostar a ponta do lápis no papel e estará representado o ponto. Vejam:
Os pontos na geometria

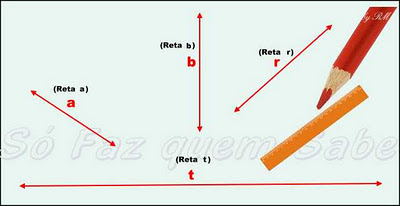
Reta

- A reta tem tamanho somente em uma direção;
- A reta tem somente uma dimensão;
- Se esticarmos um fio de linha bem esticadinho, teremos a noção de um “pedaço” de reta;
- Se esse fio de linha for pego de um carretel gigantesco, for infinito, não tiver começo nem fim, nos dará a idéia de uma reta;
- Como toda figura geométrica, a reta é formada por pontos, por infinitos pontos. A reta é um conjunto cujos elementos são pontos.
- Geralmente para se indicar as retas, usam-se as letras minúsculas do nosso alfabeto: a, b, c, r, s, t, etc.
- É fácil representar as imagens de retas. Com um lápis, um papel e uma régua, é só traçar uma linha e estará representada a reta. Vejam:
As retas e a geometria

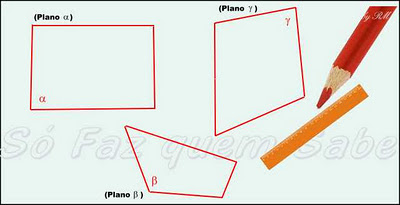
Plano

- O plano tem tamanho em duas direções;
- O plano tem duas dimensões;
- Se olharmos uma folha de papel, teremos a noção de um pedaço de um plano;
- Se esse papel fosse gigantesco, não tivesse nem fim nem começo em qualquer lado que olhássemos, teríamos a idéia de um plano;
- Como toda figura geométrica, o plano é formado por pontos, por infinitos pontos. O plano é um conjunto cujos elementos são pontos.
- Geralmente para se indicar os planos, usam-se as letras minúsculas do alfabeto grego: (alfa), (beta), (gama), (delta), etc.
- Podemos representar as imagens de planos, desenhando na folha de papel, partes da própria folha de papel. Vejam:
O plano na geometria

Fixando o Conceito

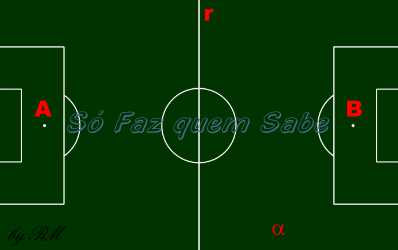
- Veja o desenho de um campo de futebol:
O plano, a reta e os pontos em um campo de futebol

- O piso do gramado nos dá idéia de plano. O plano (alfa).
- A linha que divide o gramado em duas partes nos dá idéia de reta. A reta r.
- As duas marcas de pênalti nos dão idéia de pontos. Os pontos A e B.

Uma Constatação

- Por dois pontos distintos passa uma única reta;
- Isso nos leva a concluir que para Determinar uma Reta, bastam apenas dois pontos.
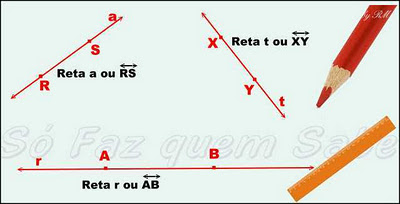
- Por isso, geralmente denominamos uma reta r qualquer que passa pelos pontos A e B, também por reta AB. Vejam os exemplos:
Bastam apenas dois pontos para determinar uma reta

Uma Definição

- Dois ou mais pontos que pertencem à mesma reta são chamados colineares, ou seja, estão na mesma linha. Veja os exemplos:
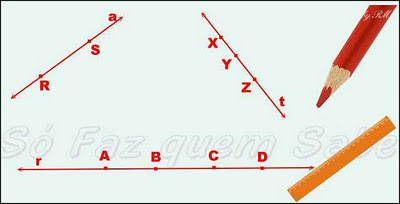
Dois ou mais pontos que pertencem à mesma reta são chamados colineares.

- Desse modo, como A, B, C e D pertencem à reta r, dizemos que A, B, C e D são colineares e, portanto a reta r passa pelos pontos A, B, C e D.
- Da mesma maneira, como X, Y e Z pertencem à reta t, dizemos que X, Y e Z são colineares e que a reta t passa pelos pontos X, Y e Z.
- Analogamente, com R e S pertencem à reta a, podemos dizer que R e S são colineares e que a reta a passa pelos pontos R e S.

Artigos Recomendados:





- Equação Geral Da Reta
Geometria Analítica demonstram que uma reta possui representação geométrica no plano cartesiano e pode ser representada por uma equação. Euclides, em seus teoremas e postulados, fundamentalizava que uma reta passa por infinitos pontos e que por...

- Equação Geral Da Reta
Geometria Analítica demonstram que uma reta possui representação geométrica no plano cartesiano e pode ser representada por uma equação. Euclides, em seus teoremas e postulados, fundamentalizava que uma reta passa por infinitos pontos e que por...

- Equação Da Reta
Toda reta não-vertical (reta que possui inclinação diferente de 90º) possui uma equação que representa todos os seus pontos. Essa equação é demonstrada através de um ponto pertencente a essa reta mais o seu coeficiente angular (m). Considere...

- Geometria
A geometria estuda as formas e as dimensões das figuras geométricas. Em geometria o ponto não possui dimensões, para representá-lo basta fazer uma marca no papel. A reta é imaginada sem espessura, sem começo, nem fim e é ilimitada nos dois sentidos,...

- Alinhamento De Três Pontos
Sabemos que com dois pontos formamos uma reta, mas três pontos só irão formar uma reta se estiverem alinhados, ou seja, deverão ser colineares. Uma das formas de verificar a condição de alinhamento de três pontos é graficamente, mas não é tão...



Matemática








.