Matemática

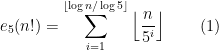

Exemplo:  . O expoente de
. O expoente de 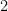 da factorização em primos de
da factorização em primos de  é igual a:
é igual a:

enquanto que o exponente de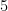 é igual a:
é igual a:

?
 Este teorema também é conhecido pelo nome de teorema de Legendre.
Este teorema também é conhecido pelo nome de teorema de Legendre.
 Para todo o inteiro
Para todo o inteiro  o expoente do primo
o expoente do primo 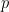 da factorização em primos de
da factorização em primos de  é igual a:
é igual a: 
- Número De Divisores Positivos De Um Número Natural
Por Profº Paulo Marques Os divisorespositivos de um número natural n são todos os números naturais p > 0 tais que n dividido por p resulta num outro número natural m. Diz-se então que p divide n e...
- Binômio De Newton
O binômio de Newton é uma maneira de expressar o desenvolvimento de um binômio na forma (a + b)n, com "n" natural.(a + b)0 = 1 (a + b)1 = a + b (a + b)2 = a2 + 2 . a . b + b2 (a + b)3 = a3 + 3 . a2 . b...
- Potenciação De Números
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...
- M.d.c) E (m.m.c).
O maior dos divisores comuns de dois ou mais números chama-se máximo divisor comum (m.d.c) exemplos consideremos os conjuntos dos divisores de 12 e 18 D12 = { 1,2,3,4,6,12} D18 = { 1,2,3,6,9,18} Os mesmos divisores ou números que aparecem em D12 e...
- PotenciaÇÃo E RadiciaÇÃo
Consideremos uma multiplicação em que todos os fatores são iguais Exemplo 5x5x5, indicada por 5³ ou seja , 5³= 5x5x5=125 onde : 5 é a base (fator que se repete) 3 é o expoente ( o número de vezes que repetimos a base) 125 é a potência ( resultado...
Matemática
Números de Zeros Finais de n Fatorial, n!

Autor: Profº Americo Tavares - http://problemasteoremas.wordpress.com/ (Grifo meu)
O número de zeros finais de  é igual ao expoente de
é igual ao expoente de 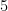 da factorização em números primos de
da factorização em números primos de  , o qual é um caso particular da Fórmula de Polignac
, o qual é um caso particular da Fórmula de Polignac 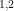 geral, sendo dado por:
geral, sendo dado por:
Pela mesma fórmula o exponente de 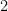 desa factorização é:
desa factorização é:
Para todo o  existe um
existe um 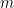 tal que
tal que 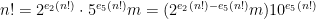 , o que conjuntamente com a demonstração apresentada na nota
, o que conjuntamente com a demonstração apresentada na nota 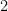 mostra a validade de
mostra a validade de  .
.
enquanto que o exponente de
Assim, o número de zeros finais de 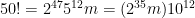 é igual a
é igual a 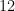 .
.
Este expoente obtém-se adicionando aos números entre 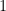 e
e  que são dvisíveis por
que são dvisíveis por 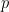 o número dos que são divisíveis por
o número dos que são divisíveis por  , depois os que são de
, depois os que são de  , e assim sucessivamente. Este processo termina na maior potência de
, e assim sucessivamente. Este processo termina na maior potência de  .
.
- Número De Divisores Positivos De Um Número Natural
Por Profº Paulo Marques Os divisorespositivos de um número natural n são todos os números naturais p > 0 tais que n dividido por p resulta num outro número natural m. Diz-se então que p divide n e...
- Binômio De Newton
O binômio de Newton é uma maneira de expressar o desenvolvimento de um binômio na forma (a + b)n, com "n" natural.(a + b)0 = 1 (a + b)1 = a + b (a + b)2 = a2 + 2 . a . b + b2 (a + b)3 = a3 + 3 . a2 . b...
- Potenciação De Números
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...
- M.d.c) E (m.m.c).
O maior dos divisores comuns de dois ou mais números chama-se máximo divisor comum (m.d.c) exemplos consideremos os conjuntos dos divisores de 12 e 18 D12 = { 1,2,3,4,6,12} D18 = { 1,2,3,6,9,18} Os mesmos divisores ou números que aparecem em D12 e...
- PotenciaÇÃo E RadiciaÇÃo
Consideremos uma multiplicação em que todos os fatores são iguais Exemplo 5x5x5, indicada por 5³ ou seja , 5³= 5x5x5=125 onde : 5 é a base (fator que se repete) 3 é o expoente ( o número de vezes que repetimos a base) 125 é a potência ( resultado...
