Matemática
Demonstração Analítica
O ponto médio $M_1$ do segmento $\overline{AB}$ é dado por:
$$M_1\left (\frac{x_A+x_B}{2},\frac{y_A+y_B}{2}\right)$$
E o ponto médio $M_2$ do segmento $\overline{BC}$ é dado por:
$$M_2\left (\frac{x_B+x_C}{2},\frac{y_B+y_C}{2}\right)$$
A equação de uma reta genérica que passa por um ponto $P(x_P,y_P)$ é dada por:
$$y-y_P=m(x-x_P)$$
r:y-\left (\frac{y_A+y_B}{2}\right)=m_r\left(x-\frac{x_A+x_B}{2}\right)
\end{equation}
Mas como $r \perp \overline{AB}$, temos que:
$$m_r \cdot m_{AB}=-1$$
\begin{matrix}
m_r \cdot \left(\frac{y_B-y_A}{x_B-x_A} \right)=-1\\
m_r=-\left(\frac{x_B-x_A}{y_B=y_A}\right)\\
\end{matrix}
\end{equation}
Substituindo $(2)$ em $(1)$, obtemos:
\begin{equation}
r:y-\left(\frac{y_A+y_B}{2}\right)=-\left(\frac{x_B-x_A}{y_B-y_A}\right)\left(x-\frac{x_A+x_B}{2}\right)
\end{equation}
Analogamente, a equação da reta $s$ é dada por:
\begin{equation}
s:y-\left(\frac{y_B+y_C}{2}\right)=-\left(\frac{x_C-x_B}{y_C-y_B}\right)\left(x-\frac{x_B+x_C}{2}\right)
\end{equation}
$$\left(\frac{y_C-y_A}{2}\right)=-x\left(\frac{x_B-x_A}{y_B-y_A}\right)+\left(\frac{x_B-x_A}{y_B-y_A}\right)\left(\frac{x_B+x_A}{2}\right)+x\left(\frac{x_C-x_B}{y_C-y_B}\right)-\left(\frac{x_C-x_B}{y_C-y_B}\right)\left(\frac{x_C+x_B}{2}\right)$$
$$\left(\frac{y_C-y_A}{2}\right)=x\left[\left(\frac{x_C-x_B}{y_C-y_B}\right)-\left(\frac{x_B-x_A}{y_B-y_A}\right)\right]+\left(\frac{x_B^2-x_A^2}{2(y_B-y_A)}\right)-\left(\frac{x_C^-x_B^2}{2(y_C-y_B)}\right)$$
$$\left(\frac{y_C-y_A}{2}\right)=x\left[\frac{(y_B-y_A)(x_C-x_B)-(y_C-y_B)(y_B-y_A)}{(y_C-y_A)(x_B-x_A)}\right]+\left(\frac{x_B^2-x_A^2}{2(y_B-y_A)}\right)-\left(\frac{x_C^2-x_B^2}{2(y_C-y_B)}\right)$$
$$\left(\frac{y_C-y_A}{2}\right)+\left(\frac{x_C^2-x_B^2}{2(y_C-y_B)}\right)-\left(\frac{x_B^2-x_A^2}{2(y_B-y_A)}\right)=x\left[\frac{(y_B-y_A)(x_C-x_B)-(y_C-y_B)(x_B-x_A)}{(y_C-y_B)(y_B-y_A)}\right]$$
\begin{equation}
x=\left[\left(\frac{y_C-y_B}{2}\right)+\left(\frac{x_C^2-x_B^2}{2(y_C-y_B)}\right)-\left(\frac{x_B^2-x_A^2}{2(y_B-y_A)}\right)\right]\cdot \left[\frac{(y_C-y_B)(y_B-y_A)}{(y_B-y_A)(x_C-x_B)-(y_C-y_B)(x_B-x_A)}\right]
\end{equation}
Utilizando a expressão $(5)$, temos:
$$x=\left[\left(\frac{-1-3}{2}\right)+\left(\frac{3^2-6^2}{2(-1-2)}\right)-\left(\frac{6^2-5^2}{2(2-3)}\right)\right]\cdot \left[\frac{(-1-2)(2-3)}{(2-3)(3-6)-(-1-2)(6-5)}\right]$$
$$x=4$$
$$y=1$$
Logo, o centro da circunferência é dado por $O(4,1)$.
r^2=(5-4)^2+(3-1)^2\\
r=\sqrt{5}\\
\end{matrix}
Da equação geral da reta temos:
\begin{equation}
x^2+y^2+Ex+Fy+G=0
\end{equation}
x_A^2+y_A^2+Ex_A+Fy_A+G=0\\
x_B^2+y_B^2+Ex_B+Fy_B+G=0\\
x_C^2+y_C^2+Ex_C+Fy_C+G=0
\end{matrix}\right.$$
onde:
$$D=\begin{vmatrix}
x_A&y_A&1\\
x_B&y_B&1\\
x_C&y_C&1
\end{vmatrix},
D_A=\begin{vmatrix}
-x_A^2-y_A^2&y_A&1\\
-x_B^2-y_B^2&y_B&1\\
-x_C-y_C^2&y_C&1
\end{vmatrix},
\qquad
D_B=\begin{vmatrix}
x_A&-x_A^2-y_A^2&1\\
x_B&-x_B^2-y_B^2&1\\
x_C&-x_C^2-y_C^2&1
\end{vmatrix},
D_C=\begin{vmatrix}
x_A&y_A&-x_A^2-y_A^2\\
x_B&y_B&-x_B^2-y_B^2\\
x_C&y_C&-x_C^2-y_C^2
\end{vmatrix}$$
Substituindo na equação $(6)$:
$$x^2+\frac{D_A}{D}x+y^2+\frac{D_B}{D}y=-\frac{D_C}{D}$$
$$\left(x^2+\frac{2D_A}{2D}x+\frac{D^2_A}{4D^2}\right)+\left(y^2+\frac{2D_B}{2D}y+\frac{D^2_B}{4D^2}\right)=\frac{D^2_A}{4D^2}+\frac{D^2_B}{4D^2}-\frac{D_C}{D}$$
$$\left(x+\frac{D_A}{2D}\right)^2+\left(y+\frac{D_B}{2D}\right)^2=\frac{D^2_A+D^2_B-4DD_C}{4D^2}$$
De modo que as coordenadas $x_O$ e $y_O$ são:
\begin{equation}
x_O=-\frac{D_A}{2D} \qquad \text{e} \qquad y_O=-\frac{D_B}{2D}
\end{equation}
Vejam que o raio $r$ é dado pela expressão:
\begin{equation}
r=\sqrt{\frac{D_A^2+D_B^2-4DD_C}{4D^2}}
\end{equation}
Veja mais:
Os $10$ Problemas de Apolônio
Como Encontrar o Centro de uma Circunferência
A Equação da Circunferência Através de um Determinante 4x4 no blog Fatos Matemáticos

- Resolução Da Integral $\displaystyle \int \frac{x^2+1}{x^2-1}dx$
Nesta postagem, veremos que: \begin{equation*} \int \frac{x^2+1}{x^2-1}dx = x+ \ln|x-1|- \ln|x+1| + C \end{equation*} onde $x \in \mathbb{R}$, sendo $x \neq \pm 1$. Seja a integral: \begin{equation*} I = \int \frac{x^2+1}{x^2-1}dx \end{equation*} Decompomos...
- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Resolução Da Integral $ \int \text{sen}(3x) \text{sen}(5x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma produto de senos em uma subtração de cossenos. Seja a integral: \begin{equation} I = \int \text{sen}(3x)...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
Matemática
Os $10$ Problemas de Apolônio: Problema $1:[PPP]$ Problema dos Três Pontos
Este é o mais simples dos problemas sobre tangências de Apolônio, que se resume em descrever uma circunferência que passa por três pontos dados não-colineares.
Sejam três pontos não-colineares quaisquer $A$, $B$ e $C$ no plano. Para descrevermos uma circunferência que passe por estes pontos, devemos encontrar o centro da circunferência.
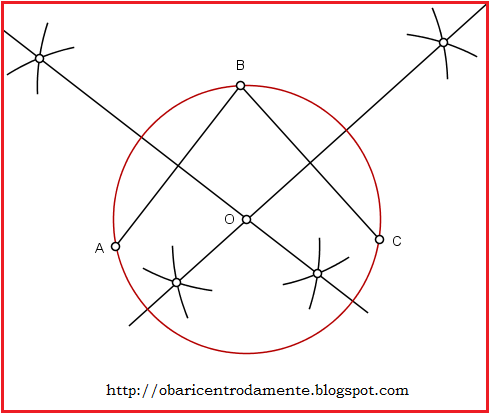
Construção Geométrica
O ponto de intersecção das mediatrizes dos segmentos $\overline{AB}$ e $\overline{BC}$ determinam o centro $O$ da circunferência $\lambda$ que passa pelos pontos $A$, $B$ e $C$, resolvendo o problema.

[Figura 1]
Vejam neste link a construção geométrica completa: Como Encontrar o Centro de uma Circunferência.
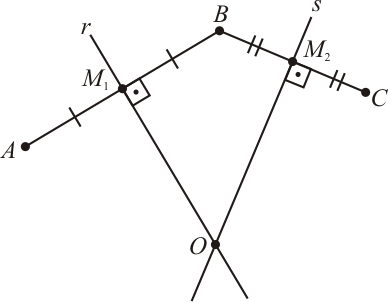
Demonstração Analítica
O centro da circunferência $\lambda$ que passa pelos pontos não-colineares $A(x_A, y_A)$, $B(x_B,y_B)$ e $C(x_C,y_C)$ é o ponto $O(x_O,y_O)$.

[Figura 2]
O ponto médio $M_1$ do segmento $\overline{AB}$ é dado por:
$$M_1\left (\frac{x_A+x_B}{2},\frac{y_A+y_B}{2}\right)$$
E o ponto médio $M_2$ do segmento $\overline{BC}$ é dado por:
$$M_2\left (\frac{x_B+x_C}{2},\frac{y_B+y_C}{2}\right)$$
A equação de uma reta genérica que passa por um ponto $P(x_P,y_P)$ é dada por:
$$y-y_P=m(x-x_P)$$
onde $m$ é o coeficiente angular da reta. Sendo assim, a equação da reta $r$ que passa pelo ponto médio $M_1$ é dada por:
\begin{equation}r:y-\left (\frac{y_A+y_B}{2}\right)=m_r\left(x-\frac{x_A+x_B}{2}\right)
\end{equation}
Mas como $r \perp \overline{AB}$, temos que:
$$m_r \cdot m_{AB}=-1$$
Esta é a condição de perpendicularidade entre duas retas, dado seus coeficientes angulares, de modo que:
\begin{equation} \begin{matrix}
m_r \cdot \left(\frac{y_B-y_A}{x_B-x_A} \right)=-1\\
m_r=-\left(\frac{x_B-x_A}{y_B=y_A}\right)\\
\end{matrix}
\end{equation}
Substituindo $(2)$ em $(1)$, obtemos:
\begin{equation}
r:y-\left(\frac{y_A+y_B}{2}\right)=-\left(\frac{x_B-x_A}{y_B-y_A}\right)\left(x-\frac{x_A+x_B}{2}\right)
\end{equation}
Analogamente, a equação da reta $s$ é dada por:
\begin{equation}
s:y-\left(\frac{y_B+y_C}{2}\right)=-\left(\frac{x_C-x_B}{y_C-y_B}\right)\left(x-\frac{x_B+x_C}{2}\right)
\end{equation}
As coordenadas do ponto $O(x_O,y_O)$ são obtidas resolvendo o sistema linear formado pelas expressões $(3)$ e $(4)$. Fazendo $(3)-(4)$, obtemos:
$$\left(\frac{y_C+y_B}{2}\right)-\left(\frac{y_B-y_A}{2}\right)=-\left(\frac{x_B-x_A}{y_B-y_A}\right)\left(x-\frac{x_B+x_A}{2}\right)+\left(\frac{x_C-x_B}{y_C-y_B}\right)\left(x-\frac{x_C+x_B}{2}\right)$$$$\left(\frac{y_C-y_A}{2}\right)=-x\left(\frac{x_B-x_A}{y_B-y_A}\right)+\left(\frac{x_B-x_A}{y_B-y_A}\right)\left(\frac{x_B+x_A}{2}\right)+x\left(\frac{x_C-x_B}{y_C-y_B}\right)-\left(\frac{x_C-x_B}{y_C-y_B}\right)\left(\frac{x_C+x_B}{2}\right)$$
$$\left(\frac{y_C-y_A}{2}\right)=x\left[\left(\frac{x_C-x_B}{y_C-y_B}\right)-\left(\frac{x_B-x_A}{y_B-y_A}\right)\right]+\left(\frac{x_B^2-x_A^2}{2(y_B-y_A)}\right)-\left(\frac{x_C^-x_B^2}{2(y_C-y_B)}\right)$$
$$\left(\frac{y_C-y_A}{2}\right)=x\left[\frac{(y_B-y_A)(x_C-x_B)-(y_C-y_B)(y_B-y_A)}{(y_C-y_A)(x_B-x_A)}\right]+\left(\frac{x_B^2-x_A^2}{2(y_B-y_A)}\right)-\left(\frac{x_C^2-x_B^2}{2(y_C-y_B)}\right)$$
$$\left(\frac{y_C-y_A}{2}\right)+\left(\frac{x_C^2-x_B^2}{2(y_C-y_B)}\right)-\left(\frac{x_B^2-x_A^2}{2(y_B-y_A)}\right)=x\left[\frac{(y_B-y_A)(x_C-x_B)-(y_C-y_B)(x_B-x_A)}{(y_C-y_B)(y_B-y_A)}\right]$$
\begin{equation}
x=\left[\left(\frac{y_C-y_B}{2}\right)+\left(\frac{x_C^2-x_B^2}{2(y_C-y_B)}\right)-\left(\frac{x_B^2-x_A^2}{2(y_B-y_A)}\right)\right]\cdot \left[\frac{(y_C-y_B)(y_B-y_A)}{(y_B-y_A)(x_C-x_B)-(y_C-y_B)(x_B-x_A)}\right]
\end{equation}
Exemplo $1$: Dados três pontos não-colineares $A(5,3)$, $B(6,2)$ e $C(3,-1)$, encontre as coordenadas do centro $O(x_O,y_O)$ e o raio da circunferência que passa por estes pontos.
Utilizando a expressão $(5)$, temos:
$$x=\left[\left(\frac{-1-3}{2}\right)+\left(\frac{3^2-6^2}{2(-1-2)}\right)-\left(\frac{6^2-5^2}{2(2-3)}\right)\right]\cdot \left[\frac{(-1-2)(2-3)}{(2-3)(3-6)-(-1-2)(6-5)}\right]$$
$$x=4$$
Substituindo o valor de $x$ na equação da reta $r$ ou $s$, encontramos o valor de $y$. Vamos tomar a equação $(3)$:
$$y-\left(\frac{3+2}{2}\right)=-\left(\frac{6-5}{2-3}\right)\left(4-\frac{5+6}{2}\right)$$$$y=1$$
Logo, o centro da circunferência é dado por $O(4,1)$.
Para determinarmos o raio, tomamos a distância do centro $O$ a quaquer um dos pontos da circunferência. Tomemos, por exemplo, o ponto $A$:
\begin{matrix}r^2=(5-4)^2+(3-1)^2\\
r=\sqrt{5}\\
\end{matrix}
Veremos a seguir um outro método que permite deduzir as expressões para as coordenadas do centro da circunferência de forma simples.
Da equação geral da reta temos:
\begin{equation}
x^2+y^2+Ex+Fy+G=0
\end{equation}
Se uma circunferência $\lambda$ passa por três pontos não-colineares $A(x_A,y_A)$, $B(x_B,y_B)$ e $C(x_C,y_C)$, então temos o sistema:
$$\left\{\begin{matrix}x_A^2+y_A^2+Ex_A+Fy_A+G=0\\
x_B^2+y_B^2+Ex_B+Fy_B+G=0\\
x_C^2+y_C^2+Ex_C+Fy_C+G=0
\end{matrix}\right.$$
Esse sistema possui três equações e três incógnitas $A$, $B$ e $C$, que podem ser obtidas através da Regra de Cramer:
$$E=\frac{D_A}{D},\qquad F=\frac{D_B}{D}, \qquad G=\frac{D_C}{D}$$onde:
$$D=\begin{vmatrix}
x_A&y_A&1\\
x_B&y_B&1\\
x_C&y_C&1
\end{vmatrix},
D_A=\begin{vmatrix}
-x_A^2-y_A^2&y_A&1\\
-x_B^2-y_B^2&y_B&1\\
-x_C-y_C^2&y_C&1
\end{vmatrix},
\qquad
D_B=\begin{vmatrix}
x_A&-x_A^2-y_A^2&1\\
x_B&-x_B^2-y_B^2&1\\
x_C&-x_C^2-y_C^2&1
\end{vmatrix},
D_C=\begin{vmatrix}
x_A&y_A&-x_A^2-y_A^2\\
x_B&y_B&-x_B^2-y_B^2\\
x_C&y_C&-x_C^2-y_C^2
\end{vmatrix}$$
Substituindo na equação $(6)$:
$$x^2+\frac{D_A}{D}x+y^2+\frac{D_B}{D}y=-\frac{D_C}{D}$$
$$\left(x^2+\frac{2D_A}{2D}x+\frac{D^2_A}{4D^2}\right)+\left(y^2+\frac{2D_B}{2D}y+\frac{D^2_B}{4D^2}\right)=\frac{D^2_A}{4D^2}+\frac{D^2_B}{4D^2}-\frac{D_C}{D}$$
$$\left(x+\frac{D_A}{2D}\right)^2+\left(y+\frac{D_B}{2D}\right)^2=\frac{D^2_A+D^2_B-4DD_C}{4D^2}$$
De modo que as coordenadas $x_O$ e $y_O$ são:
\begin{equation}
x_O=-\frac{D_A}{2D} \qquad \text{e} \qquad y_O=-\frac{D_B}{2D}
\end{equation}
Vejam que o raio $r$ é dado pela expressão:
\begin{equation}
r=\sqrt{\frac{D_A^2+D_B^2-4DD_C}{4D^2}}
\end{equation}
Exemplo $2$: Dados três pontos não-colineares $A(5,3)$, $B(6,2)$ e $C(3,-1)$, encontre as coordenadas do centro $O(x_O,y_O)$ e o raio da circunferência que passa por estes pontos.
$$D=\begin{vmatrix}
5&3&1\\
6&2&1\\
3&-1&1
\end{vmatrix}
=-6$$
$$
D_A=\begin{vmatrix}
-5^2-6^2&3&1\\
-6^2-2^2&2&1\\
-3^2-(-1)^2&-1&1
\end{vmatrix}
=48$$
$$D_B=\begin{vmatrix}
5&-5^2-3^2&1\\
6&-6^2-2^2&1\\
3&-3^2-(-1)^2&1
\end{vmatrix}
=12$$
$$x_O=-\frac{D_A}{2D}=-\frac{48}{-12}=4 \qquad \text{e} \qquad y_O=-\frac{D_B}{2D}=-\frac{12}{-12}=1$$
Logo, o centro da circunferência é dado por $O(4,1)$, que é o mesmo valor encontrado no exemplo $1$.
Para o raio $r$, devemos calcular $D_C$:
$$D_C=\begin{vmatrix}
5&3&-5^2-3^2\\
6&2&-6^2-2^2\\
3&-1&-3^2-(-1)^2
\end{vmatrix}
=-72$$
Agora, usamos a expressão $(8)$:
$$r=\sqrt{\frac{48^2+12^2-4(-6)(-72)}{4(-6)^2}}=\sqrt{5}$$
Deixo meus agradecimentos ao Professor Paulo Sérgio, articulador do blog Fatos Matemáticos.
$$D=\begin{vmatrix}
5&3&1\\
6&2&1\\
3&-1&1
\end{vmatrix}
=-6$$
$$
D_A=\begin{vmatrix}
-5^2-6^2&3&1\\
-6^2-2^2&2&1\\
-3^2-(-1)^2&-1&1
\end{vmatrix}
=48$$
$$D_B=\begin{vmatrix}
5&-5^2-3^2&1\\
6&-6^2-2^2&1\\
3&-3^2-(-1)^2&1
\end{vmatrix}
=12$$
$$x_O=-\frac{D_A}{2D}=-\frac{48}{-12}=4 \qquad \text{e} \qquad y_O=-\frac{D_B}{2D}=-\frac{12}{-12}=1$$
Logo, o centro da circunferência é dado por $O(4,1)$, que é o mesmo valor encontrado no exemplo $1$.
Para o raio $r$, devemos calcular $D_C$:
$$D_C=\begin{vmatrix}
5&3&-5^2-3^2\\
6&2&-6^2-2^2\\
3&-1&-3^2-(-1)^2
\end{vmatrix}
=-72$$
Agora, usamos a expressão $(8)$:
$$r=\sqrt{\frac{48^2+12^2-4(-6)(-72)}{4(-6)^2}}=\sqrt{5}$$
Deixo meus agradecimentos ao Professor Paulo Sérgio, articulador do blog Fatos Matemáticos.
Veja mais:
Os $10$ Problemas de Apolônio
Como Encontrar o Centro de uma Circunferência
A Equação da Circunferência Através de um Determinante 4x4 no blog Fatos Matemáticos

- Resolução Da Integral $\displaystyle \int \frac{x^2+1}{x^2-1}dx$
Nesta postagem, veremos que: \begin{equation*} \int \frac{x^2+1}{x^2-1}dx = x+ \ln|x-1|- \ln|x+1| + C \end{equation*} onde $x \in \mathbb{R}$, sendo $x \neq \pm 1$. Seja a integral: \begin{equation*} I = \int \frac{x^2+1}{x^2-1}dx \end{equation*} Decompomos...
- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Resolução Da Integral $ \int \text{sen}(3x) \text{sen}(5x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma produto de senos em uma subtração de cossenos. Seja a integral: \begin{equation} I = \int \text{sen}(3x)...
- Integral De $1/(1+x^2)^2dx$
Considere a integral: $$\int \left ( \frac{1}{1+x^2} \right )^2$$ Para resolvê-la, utilizamos uma substiruição trigonométrica, fazendo: \begin{matrix} x&=&\tan(u)\\ dx&=&\sec^2(u)du\\ \end{matrix} Assim temos: \begin{equation} \int...
