POLÍGONOS
Matemática

POLÍGONOS





CONSIDERAÇÕES INICIAIS

Superfície de polígono é a reunião do polígono com o seu interior.

Área de um polígono é a medida de superficie desse polígono.

Nota: Por comodidade, a área da superficie de um poligonoserá denominada área de um poligono.

Dois polígonos se dizem equivalentes se têm a mesma área.


AREAS DOS PRINCIPAIS POLIGONOS



































































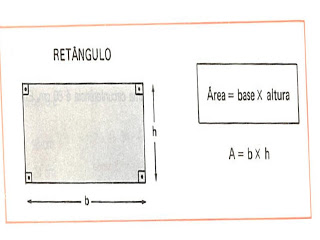
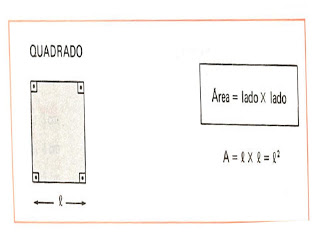
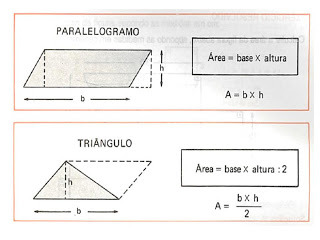
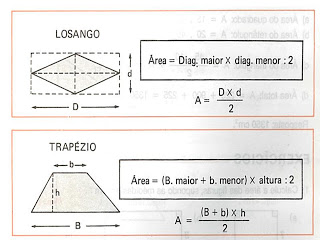
Nota:

Nas fórmulas, para facilitar,usamos apenas a palavra:
= lado em vez de medida do lado.
= base nem vez de medida da base, e assim por diante.


EXERCÍCIOS RESOLVIDOS

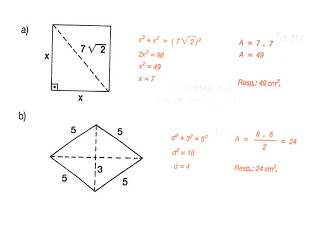
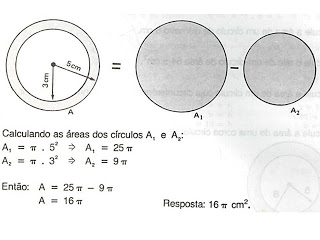
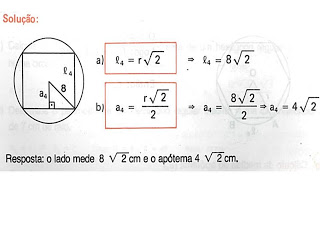
Calcular a área da figura abaixo, supondo as medidas em centimetros.


































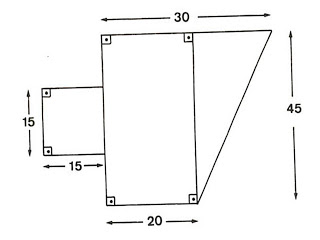
EXERCÍCIOS

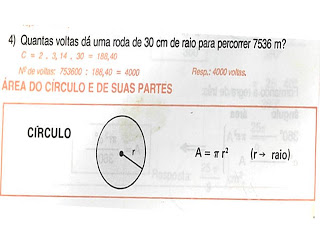
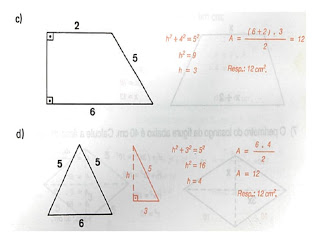
1) Calcule a área das figuras, supondo as medidas em cm:


















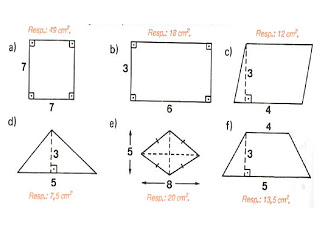
2) Calcule a área da figura, supondo as medidas em cm:

















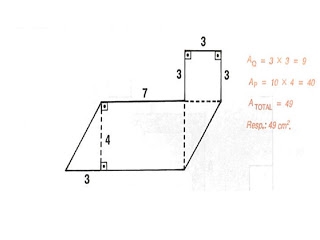
3) Calcule a área dos polígonos, supondo as medidas em cm:





































































































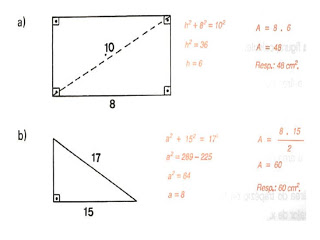
8) Calcule a área da figura sombreada, sabendo que o lado do quadrado maior mede 8m e do quadrado menor 5 m.

















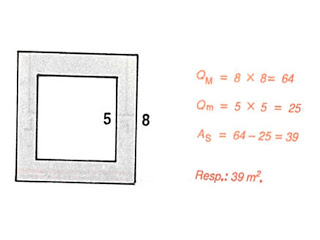
9) Calcule a áreada figura, supondo as medidas em cm:


















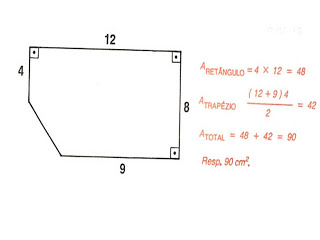
10) Calcule a área dos polígonos,supondo as medidas em cm:




16 - MEDIDA DA CIRCUNFERÊNCIA E ÁREA DO CÍRCULO

MEDIDA DA CIRCUNFERÊNCIA E ÁREA DO CÍRCULO



COMPRIMENTO DA CIRCUNFERÊNCIA

Coloque um disco numa mesa e com um barbante dê a volta completa no mesmo.
















A seguir, estique o barbante e meça o seu comprimento. VCalculando a razão entre as medidas do barbante e do diâmentro do disco, vamos ter aproximadamente:

















Logo:

O comprimento da circunferência é igual a duas vezes o pi vezes o raio da mesma .


















EXERCICIOS RESOLVIDOS
















EXERCÍCIOS
































SETOR CERCULAR































EXERCÍCIOS RESOLVIDOS

1) Calcule a área de uma coroa circular de raio 3cm e 5cm

solução













































EXERCÍCIOS














































































15 - POLÍGNOS REGULARES

POLÍGNOS REGULARES


POLÍGNO INSCRITO NUMA CIRCUNFERÊNCIA


Dizemos que o polignos é inscrito quando todos os seus vértices pertencem à circunferência.

veja:
















A circunferência está circunscrita ao polígno


POLÍGNO CIRCUNSCRITO A UMA CIRCUNFERÊNCIA

Dizemos que um poligno é circunscrito quanto todos os seus lados são tangentes à circunferência.

veja:















A circunferência está inscrita no polígno


POLÍGNO REGULARES

Um poligno é regular quando tem os lados congruentes e os ângulos congruentes.

veja:
















Os polígnos regulares podem ser inscritos ou circunscritos a uma circunferência .


APÓTEMA DE UM POLÍGNO REGULAR

















RELAÇÕES MÉTRICAS NOS POLÍGNOS REGULARES































EXERCÍCIOS RESOLVIDOS 

Calcular a medida do lado e do apótema do quadrado inscrito numa circunferência de raio 8 cm
















EXERCÍCIOS

















RAZÕES TRIGONOMÉTRICA


SENO, COSSENO E TANGENTE DE UM ÂNGULO AGUDO

No triângulo retângulo definem-se:
















































EXERCÍCIO RESOLVIDO

Calcular o seno, o cosseno e a tangente do ângulo aslfa
















Observações:

O seno e o cosseno são sempre números reais menores que 1, pois qualquer cateto é sempre menor que a hopotenusa.
A tagente é um número real positivo.


EXERCÍCIOS

1) No triângulo da figura calcule:


















2) No triângulo retângulo da figura calcule:


















3) No triângulo retângulo da figura calcule:

















TABELA DE RAZÕES TRIGONOMÉTRICAS

Os valores aproximados dos senos, cossenos e tangentes dos ângulos de 1º a 89º são encontraods na tabela a seguir.

Uso da tabela

Com a tabela podemos resolver dois tipos de problemas:

Dado o ângulo, determinar a razão trigonométrica.

exemplos:

1) Calcule sen15º
Na coluna ângulo, achamos 0,2588.
Assim sen 15º = 0,2588.

2) Calcule tg 50º
Na coluna ângulo, procuramos 50º
Na coluna tangente, achamos 1,1918
Assim tg 50º = 1,1918

Dada a razão trigonométrica, determinar o ângulo

Exemplo

Calcule o ângulo x, sendo cosx = 0,4226
Na coluna cosseno, procuramos 0,4226
Na coluna ângulo, achamos 65º
Assim x = 65º

































































EXERCÍCIOS

1) Consulte a tabela e enconctre o valor de:

















2) Consulte a tabela e responda:

















3) Consulte a tabela e determine o ângulo x:

















ÂNGULOS NOTÁVEIS

As razões trigonométricas dos ângulos de 30º, 45º e 60º aparecem frequentemente no problemas. Por isso, vamos apresentar essas razões na forma fracionária.


















EXERCÍCIOS RESOLVIDOS 

1) Calcular o valor de x no triângulo retângulo da figura abaixo.

















2) Calcular os catetos de um triângulo retângulo cuja a hipotenusa mede 6 cm e um dos ângulos mede 60º
































EXERCÍCIOS 

1) Calcule o valor de x em cada um dos triângulos:

























































































fonte:jmpgeograafia.blogspot.com.br




- Medidas De Comprimento
Para medirmos comprimento, usamos como unidade o metro, que representamos pelo símbolo m (lê-se metro). Medidas maiores que o metro 1000 m = 1 km (quilometro) 100 m = 1 (hectômetro) 10 m = 1 dam (decâmetro) Medidas menores que o metro 1 m = 10 dm...

- PolÍgnos Convexos
POLÍGNOS Plignos é um conjunto de segmentos consecutivos não colíneares no qual os extremos do primeiro e do último coincidem. Assim como já vimos para os quadriláteros, dizemos que um polígno é convexo quando qualquer segmento com extremidades...

- PolÍgonos Inscritos Na CircunferÊncia
Professor de Matemática e Ciências Antonio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] HTTP://ensinodematemtica.blogspot.com http://accbarrosogestar.blogspot.com.br  I) RESUMO DE ALGUNS POLÍGONOS...

- Apótema
Considerando um círculo e um polígono inscrito de n lados, definimos como apótema de uma figura poligonal o segmento de reta que parte do centro da figura formando com o lado um ângulo de 90º, isto é, podemos dizer que o apótema é perpendicular...

- Apótema
Considerando um círculo e um polígono inscrito de n lados, definimos como apótema de uma figura poligonal o segmento de reta que parte do centro da figura formando com o lado um ângulo de 90º, isto é, podemos dizer que o apótema é perpendicular...



Matemática








.