Matemática
O ponto comparado à circunferência pode assumir três posições diferentes, pode ser: externo à circunferência, interno à circunferência ou pertencer à circunferência.
Antes é preciso saber o que é uma circunferência, veja o desenho abaixo que distingue círculo de circunferência:
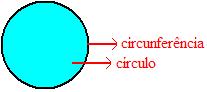
Portanto, circunferência é o contorno de um círculo. E podemos dizer que no círculo e fora dele e na própria circunferência existem infinitos pontos.
• Ponto interno à circunferência
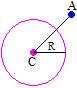
Podemos concluir que nesse caso o raio é menor que a distância do ponto A ao centro da circunferência.
Então, como dCA > R podemos escrever: (xA – a)2 + (yA – b) > R2
• Ponto externo à circunferência
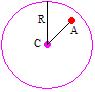
Podemos concluir que nesse caso o raio é maior que a distância do ponto A ao centro da circunferência.
Então, como dCA < R podemos escrever: (xA – a)2 + (yA – b) < R2
• Ponto pertence à circunferência
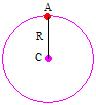
Podemos concluir que nesse caso o raio é igual à distância do ponto A ao centro da circunferência.
Então, como dCA = R podemos escrever: (xA – a)2 + (yA – b) = R2
Exemplo: Verifique qual a posição dos pontos P(0,0); Q(1,-4); R(-2,-5) em relação à circunferência de equação x2 + y2 + 2x + 8y + 13 = 0
Deve-se transformar essa equação normal em reduzida.
x2 + y2 + 2x + 8y + 13 = 0
x2 + 2x + y2 + 8y = -13
(x2 + 2x + 1) + (y2 + 8y + 16) = -13 + 1 +16
(x + 1)2 + (y + 4)2 = 4
Agora, com essa equação reduzida da circunferência, iremos substituir cada ponto os termos de x e y.
• P(0,0)
(0+ 1)2 + (0 + 4)2 = 4
12 + 42 = 4
1 + 16 = 4
17 > 4
Portanto, o ponto P é externo à circunferência
• Q(1,-4)
(1+ 1)2 + ((-4) + 4)2 = 4
22 + 02 = 4
4 = 4
Portanto, o ponto Q pertence à circunferência.
• R(-2,-5)
((-2)+ 1)2 + ((-5) + 4)2 = 4
(-1)2 + (-1)2 = 4
1 + 1 = 4
2 < 4
Portanto, o ponto R é interno à circunferência.
www.mundoeducacao.com.br
- Posições Relativas Entre Um Ponto E Uma Circunferência
Um pensamento elementar quanto à posição de um ponto em relação a uma circunferência é que esse ponto pode assumir três posições diferentes. Mas como verificar de fato a posição de um ponto no plano cartesiano em relação a uma circunferência...
- Equação Reduzida Da Circunferência
Da mesma forma que equacionamos uma reta é possível também representarmos uma circunferência na forma de equações, utilizando seu centro e um ponto genérico da circunferência. Veja a representação em um plano cartesiano de uma circunferência...
- Posição De Um Ponto Em Relação A Uma Circunferência
Posição de um ponto em relação a uma circunferênciaMarcelo Rigonatto Circunferência no planoSabemos que os pontos de uma circunferência estão a uma mesma distância do centro O(x0, y0) e que a essa distância damos o nome...
- Equação Da Circunferência
Da mesma forma que equacionamos uma reta é possível também representarmos uma circunferência na forma de equações, utilizando seu centro e um ponto genérico da circunferência. Veja a representação em um plano cartesiano de uma circunferência...
- Circunferências
CIRCUNFERÊNCIA É o conjunto dos pontos do plano cuja distância ao ponto C é igual a r. O ponto C é chamado centro da circunferência e o segmento de reta que liga um ponto qualquer dela ao centro é chamado raio da circunferência. Assim, r é a...
Matemática
Posição relativa entre ponto e circunferência
O ponto comparado à circunferência pode assumir três posições diferentes, pode ser: externo à circunferência, interno à circunferência ou pertencer à circunferência.
Antes é preciso saber o que é uma circunferência, veja o desenho abaixo que distingue círculo de circunferência:
Portanto, circunferência é o contorno de um círculo. E podemos dizer que no círculo e fora dele e na própria circunferência existem infinitos pontos.
• Ponto interno à circunferência

Podemos concluir que nesse caso o raio é menor que a distância do ponto A ao centro da circunferência.
Então, como dCA > R podemos escrever: (xA – a)2 + (yA – b) > R2
• Ponto externo à circunferência
Podemos concluir que nesse caso o raio é maior que a distância do ponto A ao centro da circunferência.
Então, como dCA < R podemos escrever: (xA – a)2 + (yA – b) < R2
• Ponto pertence à circunferência
Podemos concluir que nesse caso o raio é igual à distância do ponto A ao centro da circunferência.
Então, como dCA = R podemos escrever: (xA – a)2 + (yA – b) = R2
Exemplo: Verifique qual a posição dos pontos P(0,0); Q(1,-4); R(-2,-5) em relação à circunferência de equação x2 + y2 + 2x + 8y + 13 = 0
Deve-se transformar essa equação normal em reduzida.
x2 + y2 + 2x + 8y + 13 = 0
x2 + 2x + y2 + 8y = -13
(x2 + 2x + 1) + (y2 + 8y + 16) = -13 + 1 +16
(x + 1)2 + (y + 4)2 = 4
Agora, com essa equação reduzida da circunferência, iremos substituir cada ponto os termos de x e y.
• P(0,0)
(0+ 1)2 + (0 + 4)2 = 4
12 + 42 = 4
1 + 16 = 4
17 > 4
Portanto, o ponto P é externo à circunferência
• Q(1,-4)
(1+ 1)2 + ((-4) + 4)2 = 4
22 + 02 = 4
4 = 4
Portanto, o ponto Q pertence à circunferência.
• R(-2,-5)
((-2)+ 1)2 + ((-5) + 4)2 = 4
(-1)2 + (-1)2 = 4
1 + 1 = 4
2 < 4
Portanto, o ponto R é interno à circunferência.
www.mundoeducacao.com.br
- Posições Relativas Entre Um Ponto E Uma Circunferência
Um pensamento elementar quanto à posição de um ponto em relação a uma circunferência é que esse ponto pode assumir três posições diferentes. Mas como verificar de fato a posição de um ponto no plano cartesiano em relação a uma circunferência...
- Equação Reduzida Da Circunferência
Da mesma forma que equacionamos uma reta é possível também representarmos uma circunferência na forma de equações, utilizando seu centro e um ponto genérico da circunferência. Veja a representação em um plano cartesiano de uma circunferência...
- Posição De Um Ponto Em Relação A Uma Circunferência
Posição de um ponto em relação a uma circunferênciaMarcelo Rigonatto Circunferência no planoSabemos que os pontos de uma circunferência estão a uma mesma distância do centro O(x0, y0) e que a essa distância damos o nome...
- Equação Da Circunferência
Da mesma forma que equacionamos uma reta é possível também representarmos uma circunferência na forma de equações, utilizando seu centro e um ponto genérico da circunferência. Veja a representação em um plano cartesiano de uma circunferência...
- Circunferências
CIRCUNFERÊNCIA É o conjunto dos pontos do plano cuja distância ao ponto C é igual a r. O ponto C é chamado centro da circunferência e o segmento de reta que liga um ponto qualquer dela ao centro é chamado raio da circunferência. Assim, r é a...
