Matemática
- Resultados Possíveis E Casos Favoráveis
Todo experimento aleatório - os fenômenos casuais onde as experiências são repetidas inúmeras vezes sob condições iguais, mas não apresentam os mesmos resultados - constitui o conjunto formado por todos os resultados possíveis. Esse conjunto...
- Experimento Aleatório
Todo experimento aleatório - os fenômenos casuais onde as experiências são repetidas inúmeras vezes sob condições iguais, mas não apresentam os mesmos resultados - constitui o conjunto formado por todos os resultados possíveis. Esse conjunto...
- Probabilidade
PROBABILIDADE A história da teoria das probabilidades, teve início com os jogos de cartas, dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo da probabilidade. A teoria da probabilidade permite que se calcule...
- Probabilidade De Dois Eventos Sucessivos Ou Simultâneos
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...
- Probabilidade
PROBABILIDADE A história da teoria das probabilidades, teve início com os jogos de cartas, dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo da probabilidade. A teoria da probabilidade permite que se calcule...
Matemática
Probabilidade
Experimento
Chama-se experimento uma experiência realizada ao acaso (aleatória) para a obtenção de alguma observação de seus resultados.
Exemplos:
No lançamento de uma moeda, observar a face voltada para cima.
Retirar uma carta de um baralho e observar seu naipe.
Exemplos:
No lançamento de uma moeda, observar a face voltada para cima.
Retirar uma carta de um baralho e observar seu naipe.
Espaço Amostral (S)
O conjunto de todos os resultados possíveis de um experimento aleatório é dito espaço amostral.
Exemplos:
No lançamento de uma moeda, observar a face voltada para cima.
S = { cara, coroa }
Ao retirar uma carta de um baralho e observar seu naipe.
S = { copas, ouros, paus, espadas }
Num lançamento de um dado, observar a face voltada para cima.
S = { 1, 2, 3, 4, 5, 6 }
Exemplos:
No lançamento de uma moeda, observar a face voltada para cima.
S = { cara, coroa }
Ao retirar uma carta de um baralho e observar seu naipe.
S = { copas, ouros, paus, espadas }
Num lançamento de um dado, observar a face voltada para cima.
S = { 1, 2, 3, 4, 5, 6 }
Evento (E)
Qualquer subconjunto do espaço amostral é dito evento.
Exemplos:
No lançamento de uma moeda, observar a face voltada para cima.
E = { sair cara }
Ao retirar uma carta de um baralho e observar seu naipe.
E = { a carta é de espadas }
Exemplos:
No lançamento de uma moeda, observar a face voltada para cima.
E = { sair cara }
Ao retirar uma carta de um baralho e observar seu naipe.
E = { a carta é de espadas }
Evento certo
Evento certo é aquele que possui todos os elementos do espaço amostral.
Exemplo:
Num lançamento de um dado, a face voltada para cima ser um número menor do que 10.
E = { 1, 2, 3, 4, 5, 6 }
Evento certo é aquele que possui todos os elementos do espaço amostral.
Exemplo:
Num lançamento de um dado, a face voltada para cima ser um número menor do que 10.
E = { 1, 2, 3, 4, 5, 6 }
Evento impossível
Evento impossível ou improvável é aquele que não possui elementos do espaço amostral.
Exemplo:
Num lançamento de um dado, a face voltada para cima ser um número maior do que 10.
E =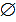
Evento impossível ou improvável é aquele que não possui elementos do espaço amostral.
Exemplo:
Num lançamento de um dado, a face voltada para cima ser um número maior do que 10.
E =
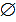
Probabilidade
Se em um fenômeno aleatório as possibilidades são igualmente prováveis, então a probabilidade de ocorrer um evento E é:
P(E) = n(E) / n(S)
Onde n(E) é o número de elementos do evento E e n(S) é o número de elementos do espaço amostral.
Exemplo:
Num lançamento de um dado, qual a probabilidade de sair um número primo?
O espaço amostral é S = { 1, 2, 3, 4, 5, 6 } e o evento é E = { 2, 3, 5 }, então:
P(E) = n(E) / n(S)
P(E) = 3/6 = 1/2 = 0,5.
P(E) = n(E) / n(S)
Onde n(E) é o número de elementos do evento E e n(S) é o número de elementos do espaço amostral.
Exemplo:
Num lançamento de um dado, qual a probabilidade de sair um número primo?
O espaço amostral é S = { 1, 2, 3, 4, 5, 6 } e o evento é E = { 2, 3, 5 }, então:
P(E) = n(E) / n(S)
P(E) = 3/6 = 1/2 = 0,5.
Propriedades
Seja A um evento e S o espaço amostral, assim sempre se tem:
1) 0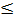 P(A)
P(A) 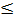 1.
1.
2) P(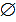 ) = 0.
) = 0.
3) P(S) = 1.
4) P(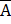 ) = 1 – P(A).
) = 1 – P(A).
1) 0
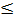 P(A)
P(A) 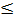 1.
1.2) P(
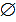 ) = 0.
) = 0.3) P(S) = 1.
4) P(
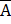 ) = 1 – P(A).
) = 1 – P(A).Probabilidade da união de dois eventos
Se A e B são eventos quaisquer de um espaço amostral, o número de elementos da ocorrência de A "ou" B é dado por:
n(A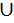 B).
B).
O número de elementos da ocorrência de A "e" B é dado por:
n(A B).
B).
A probabilidade da ocorrência de A união B é dada por:
P(A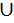 B) = P(A) + P(B) – P(A
B) = P(A) + P(B) – P(A  B).
B).
n(A
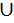 B).
B).O número de elementos da ocorrência de A "e" B é dado por:
n(A
 B).
B).A probabilidade da ocorrência de A união B é dada por:
P(A
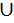 B) = P(A) + P(B) – P(A
B) = P(A) + P(B) – P(A  B).
B).Eventos mutuamente excludentes
Dois eventos A e B são ditos mutuamente excludentes ou exclusivos se a ocorrência de um impede a ocorrência do outro.
Neste caso, A B =
B = 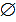 , então:
, então:
P(A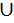 B) = P(A) + P(B).
B) = P(A) + P(B).
Exemplo:
Num lançamento de um dado, seja o evento A = { sair um número par } e o evento B = { sair um número ímpar }.
Logo, se o evento A ocorrer impede a ocorrência de B.
Assim tem-se:
S = {1, 2, 3, 4, 5, 6}; A = {2, 4, 6} e B = {1, 3, 5} e daí:
P(A) = 3/6 = 1/2 e P(B) = 3/6 = 1/2.
P(A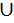 B) = 1/2 + 1/2 = 1.
B) = 1/2 + 1/2 = 1.
Neste caso, A
 B =
B = 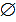 , então:
, então:P(A
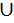 B) = P(A) + P(B).
B) = P(A) + P(B).Exemplo:
Num lançamento de um dado, seja o evento A = { sair um número par } e o evento B = { sair um número ímpar }.
Logo, se o evento A ocorrer impede a ocorrência de B.
Assim tem-se:
S = {1, 2, 3, 4, 5, 6}; A = {2, 4, 6} e B = {1, 3, 5} e daí:
P(A) = 3/6 = 1/2 e P(B) = 3/6 = 1/2.
P(A
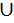 B) = 1/2 + 1/2 = 1.
B) = 1/2 + 1/2 = 1.Probabilidade condicional
Se um evento A ocorreu ou irá ocorrer, a probabilidade de outro evento B ocorrer sabendo da ocorrência de A ( onde P(A) > 0 ) é dada por:
P(B|A) = n(A B) / n(A) ou P(B/A) = P(A
B) / n(A) ou P(B/A) = P(A  B) / P(A)
B) / P(A)
Exemplo:
Lança-se dois dados, sabendo que a soma dos dois resultados foi 6, qual a probabilidade de ter sair o número 2 em um deles?
Sendo A = { a soma dois dois é 6 } e B = { sair um número primo }
A = { (1, 5); (5, 1); (2, 4); (4, 2); (3, 3) } e B = { (1, 2); (2, 1); (2, 2); (2, 3); (3, 2); (2, 4); (4, 2); (2, 5); (5, 2); (2, 6); (6, 2) }
A B = { (2, 4); (4, 2) }, daí:
B = { (2, 4); (4, 2) }, daí:
P(B|A) = n(A B) / n(A)
B) / n(A)
P(B|A) = 2 / 5.
P(B|A) = n(A
 B) / n(A) ou P(B/A) = P(A
B) / n(A) ou P(B/A) = P(A  B) / P(A)
B) / P(A)Exemplo:
Lança-se dois dados, sabendo que a soma dos dois resultados foi 6, qual a probabilidade de ter sair o número 2 em um deles?
Sendo A = { a soma dois dois é 6 } e B = { sair um número primo }
A = { (1, 5); (5, 1); (2, 4); (4, 2); (3, 3) } e B = { (1, 2); (2, 1); (2, 2); (2, 3); (3, 2); (2, 4); (4, 2); (2, 5); (5, 2); (2, 6); (6, 2) }
A
 B = { (2, 4); (4, 2) }, daí:
B = { (2, 4); (4, 2) }, daí:P(B|A) = n(A
 B) / n(A)
B) / n(A)P(B|A) = 2 / 5.
Regra da multiplicação
Como P(B/A) = P(A  B) / P(A)
B) / P(A)
Então, tem-se que:
P(A B) = P(B|A) . P(A) = P(A|B) . P(B)
B) = P(B|A) . P(A) = P(A|B) . P(B)
 B) / P(A)
B) / P(A)Então, tem-se que:
P(A
 B) = P(B|A) . P(A) = P(A|B) . P(B)
B) = P(B|A) . P(A) = P(A|B) . P(B)Propriedades
1) 0 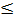 P(B|A)
P(B|A) 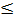 1.
1.
2) P(S|A) = 1.
3) Se B1 B2 =
B2 = 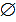 , então:
, então:
P(B1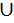 B2|A) = P(B1|A) + P(B2|A).
B2|A) = P(B1|A) + P(B2|A).
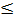 P(B|A)
P(B|A) 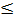 1.
1.2) P(S|A) = 1.
3) Se B1
 B2 =
B2 = 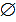 , então:
, então:P(B1
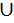 B2|A) = P(B1|A) + P(B2|A).
B2|A) = P(B1|A) + P(B2|A).Eventos independentes
Dois eventos A e B são ditos independentes se o fato de A ter ocorrido não tem qualquer efeito sobre a ocorrência de B.
Neste caso, P(B/A) = P(B).
Se A e B eventos independentes, a probabilidade de ocorrer A e B nesta ordem é:
P(A B) = P(A) . P(B).
B) = P(A) . P(B).
Exemplo:
No lançamento de dois dados, qual a probabilidade de sair 2 no 1º e 3 no 2º?
O fato de sair 2 no 1º em nada influi em sair 3 no 2º, logo são independentes.
Chamando A = { sair 2 no 1º } e B = { sair 3 no 2º }, então:
P(A B) = (1/6) . (1/6) = 1/36.
B) = (1/6) . (1/6) = 1/36.
De uma forma geral, se os eventos A1, A2, . . . , An são independentes, então:
P(A1 A2
A2  . . .
. . .  An) = P(A1) . P(A2) . . . P(An)
An) = P(A1) . P(A2) . . . P(An)
Neste caso, P(B/A) = P(B).
Se A e B eventos independentes, a probabilidade de ocorrer A e B nesta ordem é:
P(A
 B) = P(A) . P(B).
B) = P(A) . P(B).Exemplo:
No lançamento de dois dados, qual a probabilidade de sair 2 no 1º e 3 no 2º?
O fato de sair 2 no 1º em nada influi em sair 3 no 2º, logo são independentes.
Chamando A = { sair 2 no 1º } e B = { sair 3 no 2º }, então:
P(A
 B) = (1/6) . (1/6) = 1/36.
B) = (1/6) . (1/6) = 1/36.De uma forma geral, se os eventos A1, A2, . . . , An são independentes, então:
P(A1
 A2
A2  . . .
. . .  An) = P(A1) . P(A2) . . . P(An)
An) = P(A1) . P(A2) . . . P(An)Teorema de Bayes
Sejam E1, E2, E3, . . . , En, eventos mutuamente excludentes e A um evento qualquer tal que P(A) > 0, tem-se então:
P(Ek|A) = P(A|Ek) . P(Ek) /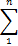 [ P(A|Ek) . P(Ek) ]
[ P(A|Ek) . P(Ek) ]
P(Ek|A) = P(A|Ek) . P(Ek) /
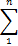 [ P(A|Ek) . P(Ek) ]
[ P(A|Ek) . P(Ek) ]Exercícios Resolvidos
R01 — No lançamento de dado qual a probabilidade de sair um número maior do que 4?
Seja o evento A = { número maior do que 4 } = { 5, 6 }, o espaço amostral é S = { 1, 2, 3, 4, 5, 6 }, então:
P(A) = n(A) / n(S) = 2 / 6 = 1/3.
P(A) = n(A) / n(S) = 2 / 6 = 1/3.
R02 — Em uma urna há 20 bolas numeradas de 1 a 20, retira-se ao acaso uma bola. Qual a probabilidade do número dela ser um múltiplo de 2 ou de 3?
Seja o evento A = { múltiplo de 2 } = { 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 } e o evento B = { múltiplo de 3 } = { 3, 6, 9, 12, 15, 18 }, logo n(A) = 10 e n(B) = 6. O número de elementos de A e B é n(A  B) = 3.
B) = 3.
P(A) = 10 / 20; P(B) = 6 / 20 e P(A B) = 3 / 20. P(A
B) = 3 / 20. P(A 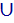 B) = 10/20 + 6/20 – 3/20 = 13/20.
B) = 10/20 + 6/20 – 3/20 = 13/20.
 B) = 3.
B) = 3.P(A) = 10 / 20; P(B) = 6 / 20 e P(A
 B) = 3 / 20. P(A
B) = 3 / 20. P(A 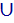 B) = 10/20 + 6/20 – 3/20 = 13/20.
B) = 10/20 + 6/20 – 3/20 = 13/20.R03 — Em uma urna há 20 bolas numeradas de 1 a 20, retira-se ao acaso uma bola. Qual a probabilidade do número dela ser um múltiplo de 3 ou de 7?
Seja A = { múltiplo de 3 }; B = { múltiplo de 7 }, entre 1 e 20, não há múltiplos em comum, logo são mutuamente excludentes e, portanto:
P(A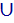 B) = 6/20 + 2/20 = 8/20 = 2/5.
B) = 6/20 + 2/20 = 8/20 = 2/5.
P(A
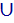 B) = 6/20 + 2/20 = 8/20 = 2/5.
B) = 6/20 + 2/20 = 8/20 = 2/5.R04 — Uma bola é retirada de uma sacola contendo 4 bolas pretas, 2 amarelas e 6 bolas vermelhas. Qual a probabilidade desta bola não ser preta?
Há 12 bolas na sacola, sendo o evento A = { a bola é preta }, então P(A) = 4/12 = 1/3.
Como se deseja que não seja preta então:
P(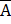 ) = 1 – 1/3 = 2/3.
) = 1 – 1/3 = 2/3.
Como se deseja que não seja preta então:
P(
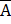 ) = 1 – 1/3 = 2/3.
) = 1 – 1/3 = 2/3.R05 — De uma urna contendo bolas numeradas de 1 a 10, retira-se duas bolas sucessivamente e sem reposição. Qual a probabilidade de ser um múltiplo de 2 e de 3, nesta ordem?
Os eventos A = { a 1ª múltiplo de 2 }; B = { a 2ª é múltiplo de 3 }.
São eventos independentes, pois a ocorrência de A em nada muda a ocorrência de B.
P(A B) = P(A) . P(B) = (5 / 10) . (3 / 10) = 15/100 = 3/20.
B) = P(A) . P(B) = (5 / 10) . (3 / 10) = 15/100 = 3/20.
São eventos independentes, pois a ocorrência de A em nada muda a ocorrência de B.
P(A
 B) = P(A) . P(B) = (5 / 10) . (3 / 10) = 15/100 = 3/20.
B) = P(A) . P(B) = (5 / 10) . (3 / 10) = 15/100 = 3/20.R06 — Um dado foi fabricado de tal forma que num lançamento a probabilidade de ocorrer um número par é o dobro da probabilidade de ocorrer número ímpar na face superior, sendo que os três números pares ocorrem com igual probabilidade, bem como os três números ímpares.
Determine a probabilidade de ocorrência de:
a) sair um número par;
b) sair o número 2 ou o número 3.
Determine a probabilidade de ocorrência de:
a) sair um número par;
b) sair o número 2 ou o número 3.
Seja A = { o número é par }; B = { o número é ímpar }. Como A  B =
B = 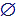 , então: P(A
, então: P(A 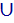 B) = P(A) + P(B) = 1
B) = P(A) + P(B) = 1
Como a probabilidade de ocorrer um número par é o dobro da de ocorrer um número ímpar P(A) = 2 . P(B), então:
2 . P(B) + P(B) = 1, logo P(B) = 1/3.
a) P(A) = 2 . P(B) = 2 . (1/3) = 2/3.
b) P(1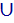 3
3 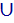 5 ) = P(1) + P(3) + P(5) = 1/3, e como:
5 ) = P(1) + P(3) + P(5) = 1/3, e como:
P(1) = P(3) = P(5), logo P(1) + P(1) + P(1) = 1/3 e daí, P(1) = 1/9 = P(3) = P(5).
Portanto, P(2) = P(4) = P(6) = 2/9.
P(2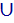 3) = P(2) + P(3) = 2/9 + 1/9 = 3/9 = 1/3.
3) = P(2) + P(3) = 2/9 + 1/9 = 3/9 = 1/3.
 B =
B = 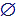 , então: P(A
, então: P(A 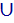 B) = P(A) + P(B) = 1
B) = P(A) + P(B) = 1Como a probabilidade de ocorrer um número par é o dobro da de ocorrer um número ímpar P(A) = 2 . P(B), então:
2 . P(B) + P(B) = 1, logo P(B) = 1/3.
a) P(A) = 2 . P(B) = 2 . (1/3) = 2/3.
b) P(1
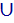 3
3 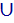 5 ) = P(1) + P(3) + P(5) = 1/3, e como:
5 ) = P(1) + P(3) + P(5) = 1/3, e como:P(1) = P(3) = P(5), logo P(1) + P(1) + P(1) = 1/3 e daí, P(1) = 1/9 = P(3) = P(5).
Portanto, P(2) = P(4) = P(6) = 2/9.
P(2
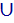 3) = P(2) + P(3) = 2/9 + 1/9 = 3/9 = 1/3.
3) = P(2) + P(3) = 2/9 + 1/9 = 3/9 = 1/3.R07 — Três moedas são lançadas ao mesmo tempo. Qual é a probabilidade de as três moedas caírem com a mesma face para cima?
Para contar o número de elementos do espaço amostral, tem-se três posições, para cada uma delas há duas opções (cara ou coroa), então: n(S) = 2 . 2 . 2 = 8.
Para terem a mesma face para cima, seria A = { (cara, cara, cara); (coroa, coroa, coroa) }, n(A) = 2.
P(A) = 2/8 = 1/4.
Para terem a mesma face para cima, seria A = { (cara, cara, cara); (coroa, coroa, coroa) }, n(A) = 2.
P(A) = 2/8 = 1/4.
R08 — Duas cartas são retiradas de um baralho sem haver reposição. Qual a probabilidade de ambas serem COPAS ou ESPADAS?
O número de elementos do espaço amostral S é dado por:
A52,2 = 52 . 51.
O número de elementos do evento "A" ambas serem de copas é dado por:
A13,2 = 13 . 12.
O número de elementos do evento "B" ambas serem de espadas é dado por:
A13,2 = 13 . 12.
P(A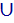 B) = (13 . 12 / 52 . 51) + (13 . 12 / 52 . 51) = 0,0588 + 0,0588 = 0,1176.
B) = (13 . 12 / 52 . 51) + (13 . 12 / 52 . 51) = 0,0588 + 0,0588 = 0,1176.
A52,2 = 52 . 51.
O número de elementos do evento "A" ambas serem de copas é dado por:
A13,2 = 13 . 12.
O número de elementos do evento "B" ambas serem de espadas é dado por:
A13,2 = 13 . 12.
P(A
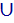 B) = (13 . 12 / 52 . 51) + (13 . 12 / 52 . 51) = 0,0588 + 0,0588 = 0,1176.
B) = (13 . 12 / 52 . 51) + (13 . 12 / 52 . 51) = 0,0588 + 0,0588 = 0,1176.R09 — Uma determinada peça é manufaturada por 3 máquinas: A, B e C. Sabe-se que A produz o dobro de peças que B e que B e C produzem o mesmo número de peças.
Sabe-se ainda que 2% das peças produzidas por A e por B são defeituosas, enquanto que 4% das produzidas por C são defeituosas.
Todas as peças produzidas são misturadas e colocadas em um depósito. Se do depósito for retirada uma peça ao acaso, qual a probabilidade de que ela seja defeituosa?
Sabe-se ainda que 2% das peças produzidas por A e por B são defeituosas, enquanto que 4% das produzidas por C são defeituosas.
Todas as peças produzidas são misturadas e colocadas em um depósito. Se do depósito for retirada uma peça ao acaso, qual a probabilidade de que ela seja defeituosa?
Considerem-se os seguintes eventos: D = { A peça é defeituosa }, A = { A peça é da máquina A }, B = { A peça é da máquina B } e C = { A peça é da máquina C }.
Tem-se então que:
P(A) = 1/2, P(B) = P(C) = 1/3.
Sabe-se também que P(D|A) = P(D|B) = 2% e que P(D|C) = 4%. Logo, tem-se:
P(D) = P(A) . P(D|A) + P(B) . P(D|B) + P(C) . P(D|C) = 0,5 . 0,02 + 0,25 . 0,02 + 0,25 . 0,04 = 2,50%.
Tem-se então que:
P(A) = 1/2, P(B) = P(C) = 1/3.
Sabe-se também que P(D|A) = P(D|B) = 2% e que P(D|C) = 4%. Logo, tem-se:
P(D) = P(A) . P(D|A) + P(B) . P(D|B) + P(C) . P(D|C) = 0,5 . 0,02 + 0,25 . 0,02 + 0,25 . 0,04 = 2,50%.
R10 — Em uma linha de produção de uma certa fábrica, determinada peça é produzida em duas máquinas.
A máquina 1, mais antiga, é responsável por 35% da produção e os 65% restantes vêm da máquina 2.
A partir dos dados passados e das informações do fabricante das máquinas, estima-se em 5% a proporção de peças defeituosas produzidas pela máquina 1 e em 2,5% a proporção de defeituosas produzidas pela máquina 2.
As peças produzidas pelas duas máquinas seguem para o departamento de armazenamento e embalagem, para venda posterior, sem distinção de qual máquina a produziu.
Se um cliente identifica uma peça defeituosa, qual é a probabilidade de que ela tenha sido produzida pela máquina 2?
A máquina 1, mais antiga, é responsável por 35% da produção e os 65% restantes vêm da máquina 2.
A partir dos dados passados e das informações do fabricante das máquinas, estima-se em 5% a proporção de peças defeituosas produzidas pela máquina 1 e em 2,5% a proporção de defeituosas produzidas pela máquina 2.
As peças produzidas pelas duas máquinas seguem para o departamento de armazenamento e embalagem, para venda posterior, sem distinção de qual máquina a produziu.
Se um cliente identifica uma peça defeituosa, qual é a probabilidade de que ela tenha sido produzida pela máquina 2?
Sejam os eventos D = { a peça é defeituosa }, M1 = { produção da máquina 1 }, M2 = { produção da máquina 2 }. Logo:
P(M1) = 0,35; P(M2) = 0,65; P(D|M1) = 0,05; P(D|M2) = 0,025; deseja-se P(M2|D), logo:
Pelo teorema de Bayes:
P(M2|D) = P(D|M2) . P(M2) / [ P(D|M1) . P(M1) + P(D|M2) . P(M2) ]
P(M2|D) = 0,025 . 0,65 / [ 0,05 . 0,35 + 0,025 . 0,65 ]
P(M2|D) = 0,01625 / 0,03375 = 0,4815.
P(M1) = 0,35; P(M2) = 0,65; P(D|M1) = 0,05; P(D|M2) = 0,025; deseja-se P(M2|D), logo:
Pelo teorema de Bayes:
P(M2|D) = P(D|M2) . P(M2) / [ P(D|M1) . P(M1) + P(D|M2) . P(M2) ]
P(M2|D) = 0,025 . 0,65 / [ 0,05 . 0,35 + 0,025 . 0,65 ]
P(M2|D) = 0,01625 / 0,03375 = 0,4815.
Exercícios Propostos
P01 — Um número natural é escolhida ao acaso entre 1 e 100. Qual a probabilidade dele não se múltiplo de 5?
P02 — Calcule a probabilidade de um piloto de automóveis vencer uma dada corrida, onde as suas "chances", segundo os entendidos, são de "3 para 2". Calcule também a probabilidade dele perder.
P03 — No lançamento dois dados. Calcule a probabilidade de ocorrer a soma 7.
P04 — Uma urna contém 10 bolas vermelhas, 6 bolas amarelas e 9 bolas pretas. Uma bola da urna é escolhida ao acaso e verifica-se que não é preta, qual a probabilidade de ser amarela?
P05 — Escolhe ao acaso um número natural entre 11 e 951. Qual a probabilidade dele ser um múltiplo de 3 ou de 5?
P06 — Seja S = {a, b, c, d}. Consideremos a seguinte distribuição de probabilidades:
P(a) = 1/8; P(b) = 1/8; P(c) = 1/4 e P(d) = x. Calcule o valor de x.
P(a) = 1/8; P(b) = 1/8; P(c) = 1/4 e P(d) = x. Calcule o valor de x.
P07 — No lançamento de 3 moedas. Qual a probabilidade de:
a) ocorrerem duas caras?
b) ocorrer pelo menos uma cara?
a) ocorrerem duas caras?
b) ocorrer pelo menos uma cara?
P08 — Um número inteiro é escolhido aleatoriamente entre 1 e 50. Qual a probabilidade de:
a) o número ser divisível por 5? b) ser divisível por 2 ou 3?
a) o número ser divisível por 5? b) ser divisível por 2 ou 3?
P09 — Uma urna A contém 4 bolas: 2 brancas e 2 pretas; uma urna B contém 5 bolas, 3 brancas e 2 pretas. Uma bola é transferida de A para B.
Uma bola é retirada de B e verifica-se ser branca. Qual a probabilidade de que a bola transferida ter sido branca?
Uma bola é retirada de B e verifica-se ser branca. Qual a probabilidade de que a bola transferida ter sido branca?
P10 — As probabilidades de três jogadores marcarem um “penalty” são, respectivamente, 2/3; 4/5 e 7/10. Se cada um “cobrar” apenas uma vez, qual a probabilidade de:
a) todos acertarem? b) apenas um acertar? c) todos errarem?
a) todos acertarem? b) apenas um acertar? c) todos errarem?
P11 — Três parafusos e três porcas estão numa caixa. Se duas peças forem retiradas ao acaso da caixa, qual a probabilidade de uma ser um parafuso e a outra ser uma porca?
P12 — As chances de um time de futebol "A" ganhar o campeonato que está disputando são de "7 para 2". Determine a probabilidade de "A" ganhar e a probabilidade de "A" perder.
P13 — De um baralho de 52 cartas retiram-se, ao acaso, duas cartas sem reposição. Qual é a probabilidade de a primeira carta ser o ÁS de paus e a segunda ser o REI de paus?
P14 — Suponha que numa turma há 6 moças e 10 rapazes. Se uma comissão de 3 pessoas é escolhida aleatoriamente, qual a probabilidade de serem selecionados:
a) 3 rapazes;
b) exatamente dois rapazes;
c) pelo menos um rapaz;
d) exatamente duas moças.
a) 3 rapazes;
b) exatamente dois rapazes;
c) pelo menos um rapaz;
d) exatamente duas moças.
P15 — Um grupo é formado por seis homens e quatro mulheres. Três pessoas são selecionadas ao acaso e sem reposição.
Qual a probabilidade de que ao menos duas sejam do sexo masculino?
Qual a probabilidade de que ao menos duas sejam do sexo masculino?
P16 — Dois dados são lançados, sejam os eventos A = {(x, y); x + y = 8}; B = {(x, y); x = y}; C = {(x, y); x + y = 10}; D = {(x, y); x > y} e E = {(x, y); x = 2y}. Calcule:
a) P(A|B) b) P(C|D) c) P(D|E) d) P(A|C) e) P(C|E)
a) P(A|B) b) P(C|D) c) P(D|E) d) P(A|C) e) P(C|E)
P17 — Três máquinas, A, B e C produzem respectivamente 40%, 50% e 10% do total de peças de uma fábrica. As percentagens de peças defeituosas nas respectivas máquinas são 3%, 5% e 2%.
Uma peça é sorteada ao acaso e verifica-se que é defeituosa. Qual a probabilidade de que ela tenha vindo da máquina B?
Uma peça é sorteada ao acaso e verifica-se que é defeituosa. Qual a probabilidade de que ela tenha vindo da máquina B?
P18 — Um grupo de 15 pessoas, dispostas da seguinte forma: 10 homens, sendo 5 menores de idade e 5 mulheres, sendo 3 menores.
Um elemento é escolhido ao acaso. Pergunta-se:
a) qual a probabilidade de ser homem?
b) qual a probabilidade de ser adulto?
c) sabendo que o escolhido foi homem, qual a probabilidade de ser adulto?
Um elemento é escolhido ao acaso. Pergunta-se:
a) qual a probabilidade de ser homem?
b) qual a probabilidade de ser adulto?
c) sabendo que o escolhido foi homem, qual a probabilidade de ser adulto?
P19 — O jogo de dominó é composto de peças retangulares formadas pela junção de dois quadrados. Em cada quadrado há a indicação de um número, representado por uma certa quantidade de bolinhas, que variam de nenhuma a seis. O número total de combinações possíveis é de 28 peças.
Se pegarmos uma peça qualquer, qual a probabilidade dela possuir ao menos um 3 ou 4 na sua face?
Se pegarmos uma peça qualquer, qual a probabilidade dela possuir ao menos um 3 ou 4 na sua face?
P20 — Em uma cidade onde carros têm que ser avaliados para controle de emissão de poluentes, 25% de todos os carros testados emitem quantidades excessivas de poluentes.
No entanto, o teste não é perfeito e pode indicar resultados errados. Desta forma, carros que emitem excesso de poluentes podem não ser detectados pelo teste e carros que não emitem excesso de poluentes podem ser considerados erroneamente fora do padrão de emissão.
Quando efetivamente testados, 99% dos carros fora do padrão são detectados e 17% dos carros em bom estado são considerados fora do padrão por erro do teste.
Qual é a probabilidade de que um carro reprovado pelo teste emita realmente excesso de poluentes?
No entanto, o teste não é perfeito e pode indicar resultados errados. Desta forma, carros que emitem excesso de poluentes podem não ser detectados pelo teste e carros que não emitem excesso de poluentes podem ser considerados erroneamente fora do padrão de emissão.
Quando efetivamente testados, 99% dos carros fora do padrão são detectados e 17% dos carros em bom estado são considerados fora do padrão por erro do teste.
Qual é a probabilidade de que um carro reprovado pelo teste emita realmente excesso de poluentes?
P21 — Duas bolas são retiradas ( com reposição ) de uma urna que contém 2 bolas brancas e 3 bolas pretas.
Qual a probabilidade de que a 1ª seja branca e a 2ª seja preta?
Qual a probabilidade de que a 1ª seja branca e a 2ª seja preta?
fonte:hpdemat.apphb.com
- Resultados Possíveis E Casos Favoráveis
Todo experimento aleatório - os fenômenos casuais onde as experiências são repetidas inúmeras vezes sob condições iguais, mas não apresentam os mesmos resultados - constitui o conjunto formado por todos os resultados possíveis. Esse conjunto...
- Experimento Aleatório
Todo experimento aleatório - os fenômenos casuais onde as experiências são repetidas inúmeras vezes sob condições iguais, mas não apresentam os mesmos resultados - constitui o conjunto formado por todos os resultados possíveis. Esse conjunto...
- Probabilidade
PROBABILIDADE A história da teoria das probabilidades, teve início com os jogos de cartas, dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo da probabilidade. A teoria da probabilidade permite que se calcule...
- Probabilidade De Dois Eventos Sucessivos Ou Simultâneos
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...
- Probabilidade
PROBABILIDADE A história da teoria das probabilidades, teve início com os jogos de cartas, dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo da probabilidade. A teoria da probabilidade permite que se calcule...
