Matemática
Definição: uma sequência numérica é chamada de Progressão Geométrica (P.G.) se o quociente entre qualquer termo (a partir do 2º) e o termo antecessor for sempre o mesmo (constante). A essa constante dá-se o nome de razão da P.G. e é representada por q.
A sequência numérica abaixo é uma P.G. Vamos verificar?
(2, 10, 50, 250, ...)
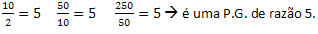
Outros exemplos:
a) ( 3, 6, 12, 24, 48, ...) é uma P.G. cuja razão é q = 2
b) ( -7, 14, -28, 56, ...) é uma P.G. de razão q = -2
c) (60, 30, 15, 15/2, ...) é uma P.G. de razão q = 1/2
d) (10, -10, 10, -10, 10, ...) é uma P.G. de razão q = -1
As Progressões Geométricas são classificadas de acordo com a razão q.
q < 0 → P.G. é alternada.
a1 > 0 e q > 1 ou a1 < 0 e 0 < q < 1 → P.G. é crescente.
a1 > 0 e 0 < q < 1 ou a1 < 0 e q > 1 → P.G. é decrescente.
Determinando o termo geral da P.G.
Qualquer termo de uma P.G. pode ser determinado quando conhecemos o 1º termo (a1) e a razão (q). Observe o processo abaixo.
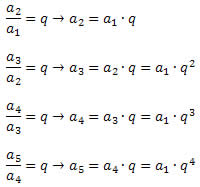
Generalizando, obtemos:
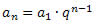
que é a fórmula do termo geral da P.G.
Exemplo 1. Determine o 10º termo da P.G. (3, 9, 27, ...).
Solução: temos que
a1 = 3 q = 9/3 = 3 a10 = ?
Usando a fórmula do termo geral, obtemos:
a10 = 3∙3(10-1)
a10 = 3∙39 = 59049
Exemplo 2. Determine o 15º termo da P.G. (-2, 10, - 50, 250, ...).
Solução: sabemos que
a1 = - 2 q = 10/(-2) = -5 a15 = ?
Vamos utilizar a fórmula do termo geral da P.G.
a15 = -2∙(-5)(15-1) = -2∙(-5)14 = -12.207.031.250
Exemplo 3. O 5º termo de uma P.G. é igual a 112 e o 1º termo é igual a 7. Determine a razão dessa P.G.
Solução: Sabemos que a5 = a1.q5 - 1
Assim,
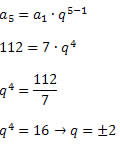
alunosonline
- Progressão Geométrica
É toda seqüência em que cada termo, a partir do segundo, é igual ao seu antecessor multiplicado por um número constante q (razão). Exemplos: a) (2, 4, 8, 16) 4 = 2.2 8 = 4.2 →a razão é 2. 16 = 8.2 b) (3, 9, 27, 81) 9 = 3.3 27 = 9.3 ...
- Progressão Geometrica
Progressão geométrica é uma seqüencia numérica que cresce ou decresce pelo produto por uma taxa constante. Nessa progressão, os seus termos a partir do segundo é igual ao produto do termo anterior por uma constante denominada razão q. Por exemplo:...
- Progressão Aritmetica
Progressão aritmética é um tipo de seqüência numérica que a partir do segundo elemento cada termo (elemento) é a soma do seu antecessor por uma constante. (5,7,9,11,13,15,17) essa seqüência é uma Progressão aritmética, pois os seus elementos...
- ProgressÃo Geometrica
Professor de Matemática no Colégio Estadual Dinah Gonçalves E Biologia na rede privada de Salvador-Bahia Professor Antonio Carlos carneiro Barroso email [email protected] HTTP://ensinodematemtica.blogspot.com.br ; ...
- Progressão Aritmética
Marcos Noé P.AA sequência numérica que envolve números reais em que a partir do 2º elemento a diferença entre qualquer termo e seu antecessor seja um número constante recebe o nome de Progressão Aritmética...
Matemática
Progressão Geométrica (P.G.)
A sequência numérica abaixo é uma P.G. Vamos verificar?
(2, 10, 50, 250, ...)
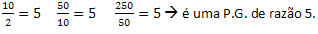
Outros exemplos:
a) ( 3, 6, 12, 24, 48, ...) é uma P.G. cuja razão é q = 2
b) ( -7, 14, -28, 56, ...) é uma P.G. de razão q = -2
c) (60, 30, 15, 15/2, ...) é uma P.G. de razão q = 1/2
d) (10, -10, 10, -10, 10, ...) é uma P.G. de razão q = -1
As Progressões Geométricas são classificadas de acordo com a razão q.
q < 0 → P.G. é alternada.
a1 > 0 e q > 1 ou a1 < 0 e 0 < q < 1 → P.G. é crescente.
a1 > 0 e 0 < q < 1 ou a1 < 0 e q > 1 → P.G. é decrescente.
Determinando o termo geral da P.G.
Qualquer termo de uma P.G. pode ser determinado quando conhecemos o 1º termo (a1) e a razão (q). Observe o processo abaixo.
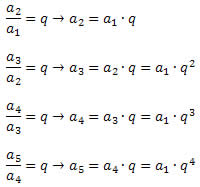
Generalizando, obtemos:
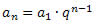
que é a fórmula do termo geral da P.G.
Exemplo 1. Determine o 10º termo da P.G. (3, 9, 27, ...).
Solução: temos que
a1 = 3 q = 9/3 = 3 a10 = ?
Usando a fórmula do termo geral, obtemos:
a10 = 3∙3(10-1)
a10 = 3∙39 = 59049
Exemplo 2. Determine o 15º termo da P.G. (-2, 10, - 50, 250, ...).
Solução: sabemos que
a1 = - 2 q = 10/(-2) = -5 a15 = ?
Vamos utilizar a fórmula do termo geral da P.G.
a15 = -2∙(-5)(15-1) = -2∙(-5)14 = -12.207.031.250
Exemplo 3. O 5º termo de uma P.G. é igual a 112 e o 1º termo é igual a 7. Determine a razão dessa P.G.
Solução: Sabemos que a5 = a1.q5 - 1
Assim,
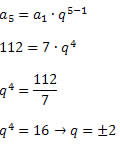
alunosonline
- Progressão Geométrica
É toda seqüência em que cada termo, a partir do segundo, é igual ao seu antecessor multiplicado por um número constante q (razão). Exemplos: a) (2, 4, 8, 16) 4 = 2.2 8 = 4.2 →a razão é 2. 16 = 8.2 b) (3, 9, 27, 81) 9 = 3.3 27 = 9.3 ...
- Progressão Geometrica
Progressão geométrica é uma seqüencia numérica que cresce ou decresce pelo produto por uma taxa constante. Nessa progressão, os seus termos a partir do segundo é igual ao produto do termo anterior por uma constante denominada razão q. Por exemplo:...
- Progressão Aritmetica
Progressão aritmética é um tipo de seqüência numérica que a partir do segundo elemento cada termo (elemento) é a soma do seu antecessor por uma constante. (5,7,9,11,13,15,17) essa seqüência é uma Progressão aritmética, pois os seus elementos...
- ProgressÃo Geometrica
Professor de Matemática no Colégio Estadual Dinah Gonçalves E Biologia na rede privada de Salvador-Bahia Professor Antonio Carlos carneiro Barroso email [email protected] HTTP://ensinodematemtica.blogspot.com.br ; ...
- Progressão Aritmética
Marcos Noé P.AA sequência numérica que envolve números reais em que a partir do 2º elemento a diferença entre qualquer termo e seu antecessor seja um número constante recebe o nome de Progressão Aritmética...