Matemática
Marcos Noé

A sequência numérica que envolve números reais em que a partir do 2º elemento a diferença entre qualquer termo e seu antecessor seja um número constante recebe o nome de Progressão Aritmética (PA). Esse valor constante é chamado de razão (r) da P.A.
Observe as Progressões Aritméticas a seguir:
(2, 4, 6, 8, 10, 12, 14, 16, 18, 20, ....), temos razão (r) igual à 2, pois 4 – 2 = 2.
(-2, 2, 6, 10, 14, 18, 22, 26, 30, ...), temos razão (r) igual à 4, pois 6 – 2 = 4.
(21, 19, 17, 15, 13, 11, 9, 7, ...), temos razão (r) igual à –2, pois 19 – 21 = –2.
Podemos classificar uma P.A. de acordo com a sua razão, se:
r > 0 , dizemos que a P.A. é crescente.
r < 0, dizemos que a P.A. é decrescente.
r = 0, P.A. constante, todos os termos são iguais.
Termo Geral de uma P.A.
Para obtermos qualquer termo de uma P.A. conhecendo o 1º termo (a1) e a razão (r) utilizamos a seguinte expressão matemática:
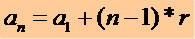
Através dessa expressão podemos escrever qualquer termo de uma P.A., veja:
a2 = a1 + r
a3 = a1 + 2r
a8 = a1+ 7r
a12 = a1 + 11r
a100 = a1 + 99r
a51 = a1 + 50r
Exemplo 1
Determine o 12º termo da P.A. (4, 9, 14, 19, 24, 29, ...).
Dados:
a1 = 4
r = 9 – 4 = 5
an = a1 + (n – 1)*r
a12 = 4 + (12 – 1)*5
a12 = 4 + 11*5
a12 = 4 + 55
a12 = 59
Exemplo 2
Dada a P.A. (18, 12, 6, 0, -6, -12, ....), calcule o 16º termo.
a1 = 18
r = 12 – 18 = – 6
an = a1 + (n – 1)*r
a16 = 18 + (16 – 1)*( –6)
a16 = 18 + 15*( –6)
a16 = 18 – 90
a16 = – 72
Soma dos Termos de uma P.A.
Podemos calcular a soma dos n primeiros termos de uma P.A., para isso basta conhecermos o 1º termo (a1) e o último termo (an). Usaremos a seguinte expressão matemática: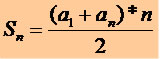
Exemplo 3
Determine a soma dos 40 primeiros termos da seguinte P.A. (3, 6, 9, 12, 15, 18, ....).
Precisamos calcular o 40º termo:
a1 = 3
r = 3
an = a1 + (n – 1)*r
a40 = 3 + (40 – 1)*3
a40 = 3 + 39*3
a40 =3 + 117
a40 =120
Agora podemos determinar a soma dos 40 primeiros termos da P.A.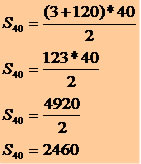
- Pa E Pg
Exercícios com PA e PG 1. Calcule a razão da P.G. onde a1 = e a8 = 48. 2. Em uma P.G. crescente tem-se a2 = 576. Calcule a razão e o 1º termo. 3. Sabendo que em uma P.G. a2 + a4 = 60 e a3 + a5 = 180, calcule a6 . 4. Somando o 1º termo com...
- Progressão Aritmetica
As atividades envolvendo progressões exigem atenção por parte dos estudantes, pois devemos ter conhecimento das fórmulas matemáticas na resolução das progressões. A partir da interpretação do enunciado deveremos escolher qual a fórmula adequada....
- Progressão Aritmetica
Progressão aritmética é um tipo de seqüência numérica que a partir do segundo elemento cada termo (elemento) é a soma do seu antecessor por uma constante. (5,7,9,11,13,15,17) essa seqüência é uma Progressão aritmética, pois os seus elementos...
- Progressão Aritmética
Definição: uma Progressão Aritmética (ou P.A.) é uma sequência numérica em que a diferença entre qualquer termo (a partir do 2º) e o termo anterior é sempre a mesma (constante). A essa constante...
- Progressão Aritmética
Progressão Aritmética é uma sequência de números reais onde cada termo, a partir do segundo, é igual ao anterior mais uma constante denominada de razão. Por exemplo, na sequência 2, 5, 8, 11, 14, 17, 20, 23, a razão é igual a 3, pois: 2 + 3...
Matemática
Progressão Aritmética
Marcos Noé

P.A
Observe as Progressões Aritméticas a seguir:
(2, 4, 6, 8, 10, 12, 14, 16, 18, 20, ....), temos razão (r) igual à 2, pois 4 – 2 = 2.
(-2, 2, 6, 10, 14, 18, 22, 26, 30, ...), temos razão (r) igual à 4, pois 6 – 2 = 4.
(21, 19, 17, 15, 13, 11, 9, 7, ...), temos razão (r) igual à –2, pois 19 – 21 = –2.
Podemos classificar uma P.A. de acordo com a sua razão, se:
r > 0 , dizemos que a P.A. é crescente.
r < 0, dizemos que a P.A. é decrescente.
r = 0, P.A. constante, todos os termos são iguais.
Termo Geral de uma P.A.
Para obtermos qualquer termo de uma P.A. conhecendo o 1º termo (a1) e a razão (r) utilizamos a seguinte expressão matemática:
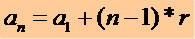
Através dessa expressão podemos escrever qualquer termo de uma P.A., veja:
a2 = a1 + r
a3 = a1 + 2r
a8 = a1+ 7r
a12 = a1 + 11r
a100 = a1 + 99r
a51 = a1 + 50r
Exemplo 1
Determine o 12º termo da P.A. (4, 9, 14, 19, 24, 29, ...).
Dados:
a1 = 4
r = 9 – 4 = 5
an = a1 + (n – 1)*r
a12 = 4 + (12 – 1)*5
a12 = 4 + 11*5
a12 = 4 + 55
a12 = 59
Exemplo 2
Dada a P.A. (18, 12, 6, 0, -6, -12, ....), calcule o 16º termo.
a1 = 18
r = 12 – 18 = – 6
an = a1 + (n – 1)*r
a16 = 18 + (16 – 1)*( –6)
a16 = 18 + 15*( –6)
a16 = 18 – 90
a16 = – 72
Soma dos Termos de uma P.A.
Podemos calcular a soma dos n primeiros termos de uma P.A., para isso basta conhecermos o 1º termo (a1) e o último termo (an). Usaremos a seguinte expressão matemática:
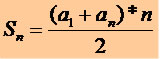
Exemplo 3
Determine a soma dos 40 primeiros termos da seguinte P.A. (3, 6, 9, 12, 15, 18, ....).
Precisamos calcular o 40º termo:
a1 = 3
r = 3
an = a1 + (n – 1)*r
a40 = 3 + (40 – 1)*3
a40 = 3 + 39*3
a40 =3 + 117
a40 =120
Agora podemos determinar a soma dos 40 primeiros termos da P.A.
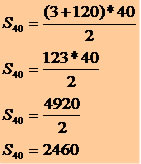
- Pa E Pg
Exercícios com PA e PG 1. Calcule a razão da P.G. onde a1 = e a8 = 48. 2. Em uma P.G. crescente tem-se a2 = 576. Calcule a razão e o 1º termo. 3. Sabendo que em uma P.G. a2 + a4 = 60 e a3 + a5 = 180, calcule a6 . 4. Somando o 1º termo com...
- Progressão Aritmetica
As atividades envolvendo progressões exigem atenção por parte dos estudantes, pois devemos ter conhecimento das fórmulas matemáticas na resolução das progressões. A partir da interpretação do enunciado deveremos escolher qual a fórmula adequada....
- Progressão Aritmetica
Progressão aritmética é um tipo de seqüência numérica que a partir do segundo elemento cada termo (elemento) é a soma do seu antecessor por uma constante. (5,7,9,11,13,15,17) essa seqüência é uma Progressão aritmética, pois os seus elementos...
- Progressão Aritmética
Definição: uma Progressão Aritmética (ou P.A.) é uma sequência numérica em que a diferença entre qualquer termo (a partir do 2º) e o termo anterior é sempre a mesma (constante). A essa constante...
- Progressão Aritmética
Progressão Aritmética é uma sequência de números reais onde cada termo, a partir do segundo, é igual ao anterior mais uma constante denominada de razão. Por exemplo, na sequência 2, 5, 8, 11, 14, 17, 20, 23, a razão é igual a 3, pois: 2 + 3...
