Matemática
Tem duas formas de provar como resolver o quadrado da soma.
A primeira é resolvendo algebricamente, veja como:
(a + b)2 é o mesmo que (a + b) . (a + b)
Então, utilizando a propriedade distributiva vamos calcular:
(a + b) . (a + b) ------ utilizando a propriedade distributiva.
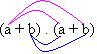
a 2 + ab + ab + b 2 ------ operar os termos semelhantes.
a 2 + 2ab + b 2
Concluímos que:
(a + b) . (a + b) = (a + b)2
A segunda forma é geometricamente, veja como:
Observe o quadrado de lado (a + b) e calculemos a sua área.
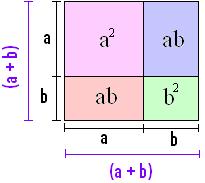

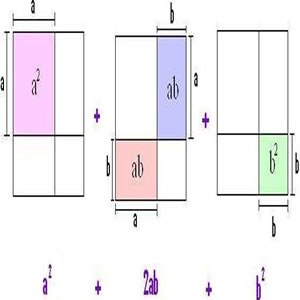
Da igualdade entre as áreas das figuras, temos:
Concluimos que (a + b)2 = a 2 + 2ab + b 2
- Quadrado Da Diferença
Professor de Matemática Antonio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] HTTP://ensinodematemtica.blogspot.com http://accbarrosogestar.blogspot.com.br Algumas multiplicações envolvendo expressões...
- Produtos Notáveis
Produtos Notáveis Mais Comuns PN1. Quadrado da soma de dois números reais a e b quaisquer – a mais b ao quadrado é igual ao quadrado do primeiro mais duas vezes o primeiro vezes o segundo, mais o quadrado do segundo: (a + b)2 = a2 + 2ab + b2 Demonstração:...
- Produtos Notaveis
Produtos notáveis são produtos de expressões algébricas que possuem uma forma geral para sua resolução. Os produtos abaixo são exemplos, em forma geral, de produtos notáveis: (a + b) . (a + b) = (a + b)2 Quadrado da soma (a – b) . (a –...
- Produtos Notáveis Mais Comuns
PN1. Quadrado da soma de dois números reais a e b quaisquer – a mais b ao quadrado é igual ao quadrado do primeiro mais duas vezes o primeiro vezes o segundo, mais o quadrado do segundo: (a + b)2 = a2 + 2ab + b2 Demonstração: Pela definição de...
- Produtos Notaveis
Produtos Notáveis Antes de iniciarmos o estudo de produtos notáveis, vamos recordar a propriedade distributiva. (a+b).(a+b) = a²+ab+ab+b² = a²+2ab+b² (a-b).(a-b) = a²-ab-ab+b² = a²-2ab+b² (a+b+c).(a+b+c)=a²+ab+ac+ab+b²+bc+ac+bc+c² Somando...
Matemática
Quadrado da soma
Tem duas formas de provar como resolver o quadrado da soma.
A primeira é resolvendo algebricamente, veja como:
(a + b)2 é o mesmo que (a + b) . (a + b)
Então, utilizando a propriedade distributiva vamos calcular:
(a + b) . (a + b) ------ utilizando a propriedade distributiva.
a 2 + ab + ab + b 2 ------ operar os termos semelhantes.
a 2 + 2ab + b 2
Concluímos que:
(a + b) . (a + b) = (a + b)2
A segunda forma é geometricamente, veja como:
Observe o quadrado de lado (a + b) e calculemos a sua área.

Da igualdade entre as áreas das figuras, temos:
Concluimos que (a + b)2 = a 2 + 2ab + b 2
(a + b)2 = quadrado do primeiro termo mais duas vezes o primeiro vezes o segundo mais o quadrado do segundo termo.
Danielle de Miranda
- Quadrado Da Diferença
Professor de Matemática Antonio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] HTTP://ensinodematemtica.blogspot.com http://accbarrosogestar.blogspot.com.br Algumas multiplicações envolvendo expressões...
- Produtos Notáveis
Produtos Notáveis Mais Comuns PN1. Quadrado da soma de dois números reais a e b quaisquer – a mais b ao quadrado é igual ao quadrado do primeiro mais duas vezes o primeiro vezes o segundo, mais o quadrado do segundo: (a + b)2 = a2 + 2ab + b2 Demonstração:...
- Produtos Notaveis
Produtos notáveis são produtos de expressões algébricas que possuem uma forma geral para sua resolução. Os produtos abaixo são exemplos, em forma geral, de produtos notáveis: (a + b) . (a + b) = (a + b)2 Quadrado da soma (a – b) . (a –...
- Produtos Notáveis Mais Comuns
PN1. Quadrado da soma de dois números reais a e b quaisquer – a mais b ao quadrado é igual ao quadrado do primeiro mais duas vezes o primeiro vezes o segundo, mais o quadrado do segundo: (a + b)2 = a2 + 2ab + b2 Demonstração: Pela definição de...
- Produtos Notaveis
Produtos Notáveis Antes de iniciarmos o estudo de produtos notáveis, vamos recordar a propriedade distributiva. (a+b).(a+b) = a²+ab+ab+b² = a²+2ab+b² (a-b).(a-b) = a²-ab-ab+b² = a²-2ab+b² (a+b+c).(a+b+c)=a²+ab+ac+ab+b²+bc+ac+bc+c² Somando...
