Matemática

Questão 21 e 22 ? Vestibulinho ETEC ? 2° Semestre de 2.014

Considere as informações para responder às questões de números 21 e 22.

Um técnico em móveis projetou uma estante conforme a figura 1.

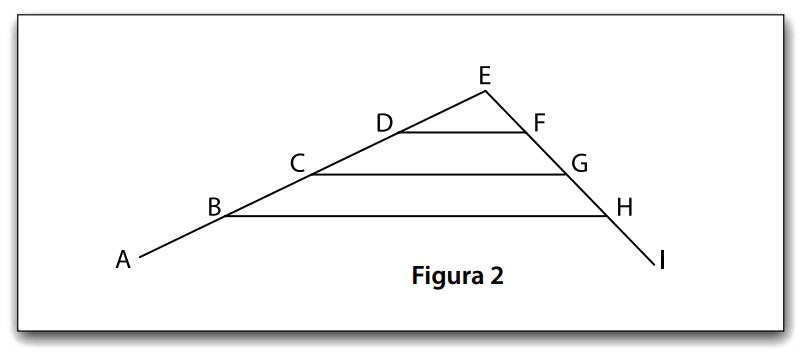
A figura 2 apresenta o esquema da parte frontal da estante.

No esquema da figura 2, tem-se que:

D é ponto médio do segmento CE;
C é ponto médio do segmento AE;
B é ponto médio do segmento AC;
F é ponto médio do segmento EG;
G é ponto médio do segmento EI;
H é ponto médio do segmento GI, e;
a medida do ângulo EIA é de 60°.

* * *

Questão 21

Se, na figura 2, a distância entre os pontos A e I for de 1,80 m, então a medida do segmento DF será, em metro,

(A) 0,55.

(B) 0,45.

(D) 0,25.

(E) 0,15.

Solução: (B)

Questão de Matemática sobre conceitos de Geometria: semelhança de triângulos.

O enunciado não cita, mas segundo o pouco que sabemos sobre construções de estantes as prateleira ficam na horizontal, logo são paralelas ao chão.

Portanto ao construir o segmento de reta AI que representa o chão obtemos um triângulo AEI (vide Figura 3).

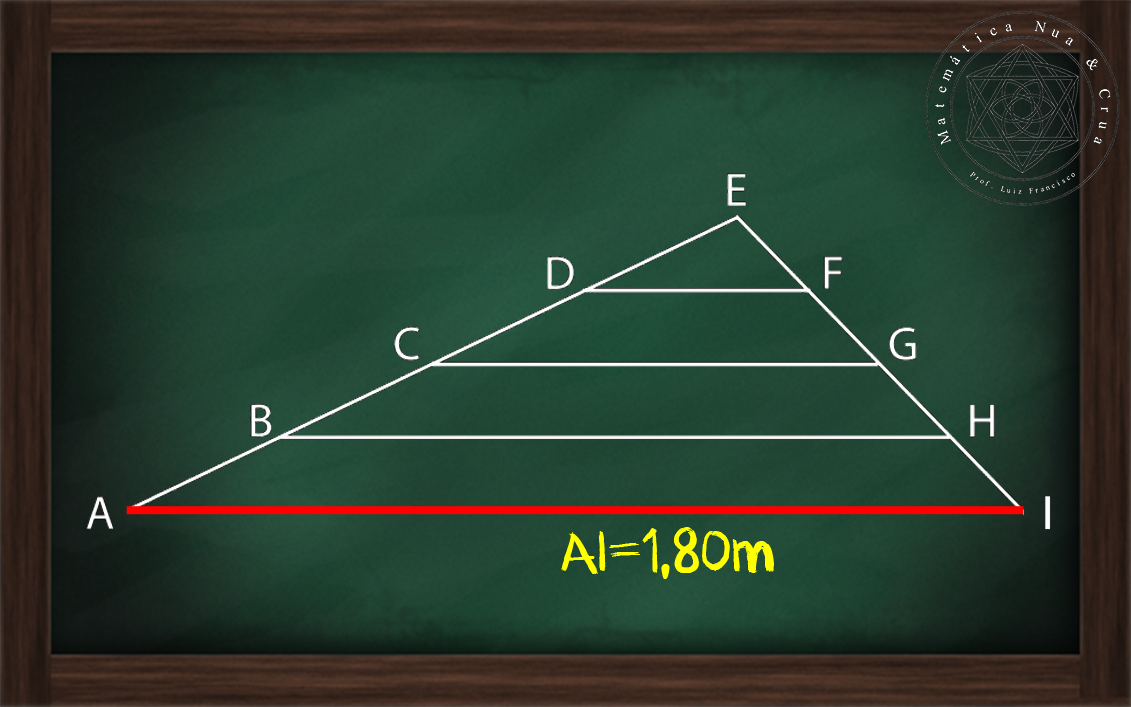Figura 3: Construção do segmento AI que representa o chão.

O ponto C é ponto médio do segmento de reta AE, logo o segmento CE tem a metade da medida do segmento AE. O ponto D é ponto médio do segmento CE, logo DE tem a metade da medida do segmento CE.

De maneira análoga, o ponto G é ponto médio do segmento de reta IE, logo o segmento GE tem a metade da medida do segmento IE. O ponto F é ponto médio do segmento GE, logo FE tem a metade da medida do segmento GE.

Então o segmento de reta DE é 1/4 da medida do segmento de reta AE, da mesma forma o segmento FE é 1/4 da medida do segmento de reta IE.

Sabemos então que no vértice E temos um ângulo é que o mesmo para o triângulo AEI e DEF sabemos também que o segmento de reta DE é proporcional ao segmento de reta AE, da mesma forma que o semento de reta FE é proporcional ao semento de reta IE.

Temos um critério de semelhança entre triângulos que diz: "se dois lados de um triângulo são proporcionais aos lados homólogos do outro triângulo e se o ângulo entre estes lados for congruente ao correspondente do outro triângulo, então os triângulos são semelhantes."

Então o triângulo AEI é semelhante ao triângulo DEF. Se são semelhantes os seus lados homólogos (lados correspondentes) são proporcionais. Já sabemos que os lados DE e FE são 1/4 da medida dos seus lados correspondentes, logo o lado DF é 1/4 da medida do lado AI.

DF = 1/4 ? (1,80 m) = 0,45 m

* * *

Questão 22

Se, na figura 2, a medida do segmento El for de 2 m, então a altura do triângulo AEI relativa ao lado Al será aproximadamente, em metro(s),

(A) 0,43.

(B) 0,87.

(D) 1,74.

(E) 3,46.

Adote:

sen 60° = 0,87
cos 60° = 0,50

Solução: (D)

Questão de Matemática sobre conceitos de Geometria: relações trigonométricas no triângulo retângulo.

A altura do triângulo AEI relativa ao lado Al é o segmento de reta que parte de do ponto E e toca perpendicularmente o lado AI.

Na Figura 4 mostramos este segmento indicando que toca o lado AI no ponto P. Como o segmento de reta EP é perpendicular ao segmento de reta AI o ângulo EPI é igual a 90°, portanto o triângulo IPE é um triângulo retângulo, reto no ponto P.

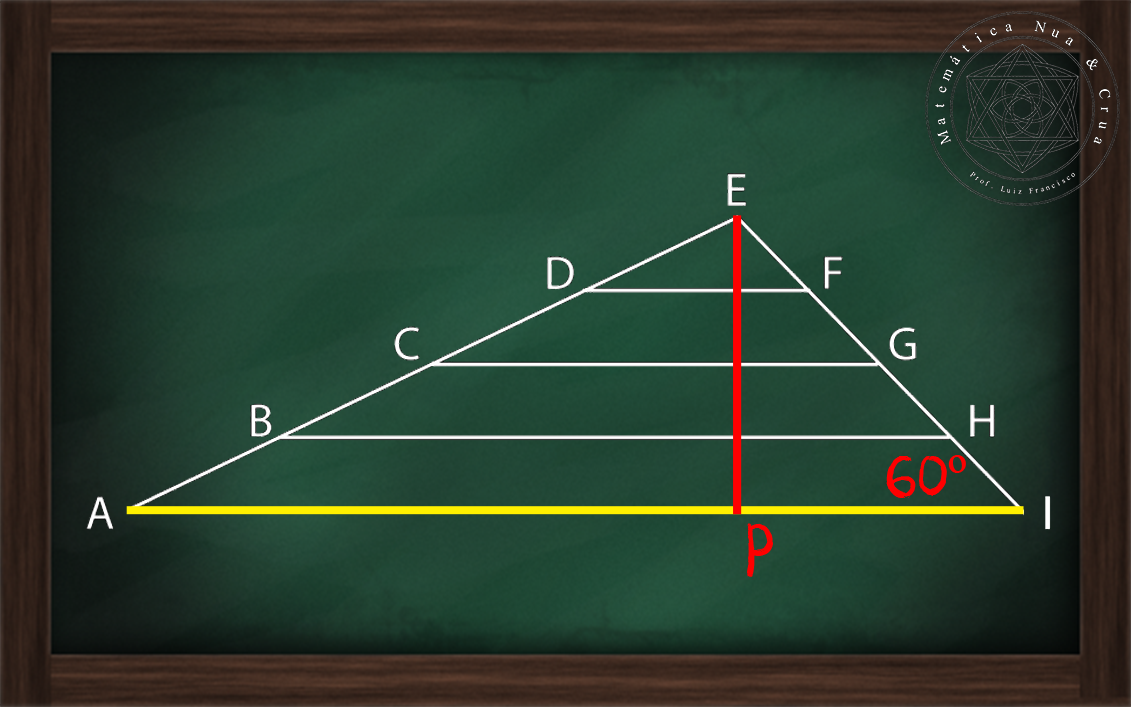Figura 4: Localização da altura do triângulo AEI e localização dos dados necessários para resolução da questão.

A altura do triângulo AEI é o cateto PE do triângulo retângulo IPE. O cateto PE é oposto ao ângulo EIA de medida 60°.

Sabemos que cosseno de um ângulo é o quociente entre a medida do cateto oposto pela hipotenusa, então

sen 60° = (cateto oposto) / hipotenusa = PE / EI

0,87 = PE / 2,00 m ? PE = 0,87 ? 2,00 m = 1,74 m

- Questão 67 ? Prova Do Estado ? (ofa) 2.010 ? Professor De Educação Básica Ii
Um professor solicitou que seus alunos provassem a proposição: ?Todo ponto da mediatriz de um segmento é equidistante dos extremos desse segmento?. Um dos alunos apresentou a seguinte sequência de argumentos: Seja o segmento AB e seja m a sua mediatriz,...

- Questão 74 ? Prova Do Estado ? (ofa) 2.011
Dados, num plano cartesiano, as coordenadas dos vértices de um triângulo retângulo, a demonstração de que o ponto médio da hipotenusa está a uma mesma distância de cada um dos vértices deste triângulo envolve apenas o uso: (A) dos coeficientes...

- Ponto Médio De Um Segmento No Plano
Ponto médio de um segmento no planoMarcelo Rigonatto Cálculo do ponto médioO segmento de reta é um subconjunto da reta, é parte da reta. Ao contrário da reta, o segmento é finito, possuindo começo e fim, podendo ser medido....

- Área Do Triângulo Equilátero
A área de um triângulo pode ser determinada através da aplicação da seguinte fórmula: Para aplicá-la é preciso ter o valor da base e da altura de um triângulo, sendo assim, uma fórmula de fácil utilização quando o triângulo for retângulo....

- Elementos De Um Triângulo
Elementos de um Triângulo Marcos Noé TriângulosOs triângulos são formados por lados, vértices, ângulos internos e externos. Neles também determinamos outros elementos mais notáveis, como mediana, altura, bissetriz, incentro,...

Matemática