Matemática
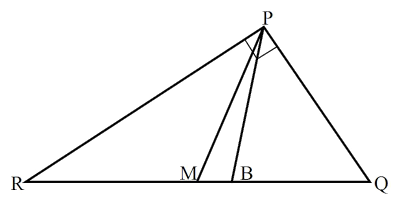
A distância entre os pontos M e B é igual a
(A) 30 / 7.
Solução: (C)
Antes de resolver gostaria de pedir desculpas, pois tenho a incrível capacidade de sempre escolher o caminho mais longo na resolução.
A medida da mediana relativa a hipotenusa de um triangulo retângulo é igual a metade da medida da hipotenusa.
h2 = c2 + c2 ? RQ2 = PR2 + PQ2 ? RQ2= 122 + 92 = 225 ?RQ = ?225 = 15
A medida de PM = RQ / 2 = 15 / 2.
Para determinar a medida da bissetriz PB inicialmente traçamos por B o segmento BA paralelo a um dos catetos, neste caso utilizamos o cateto PQ (vide, Fig. 1). O triângulo RAB é semelhante ao triângulo RPQ, portanto:
PA = BA
PA = BA = PB / ?2 = PB ? ?2 / 2
RA = PR ? PA
Sendo o triângulo RAB e o triângulo RPQ semelhantes, temos a seguinte relação:
PQ / BA = PR / RA ? PQ / BA = PR / (PR ? PA)
Resolvemos obtemos:
PQ ? (PR ? PA) = PR ? BA ? PR ? BA = PQ ? PR ? PQ ? PA ?
? PR ? (PB ? ?2 / 2) = PQ ? PR ? PQ ? (PB ? ?2 / 2) ?
? PR ? (PB ? ?2 / 2) + PQ ? (PB ? ?2 / 2) = PQ ? PR ?
? PB ? (?2 / 2) ? (PR + PQ) ? = PQ ? PR ? PB ? (?2 / 2) = (PQ ? PR) / (PR + PQ) ?
? PB = (2 ? PQ ? PR) / (?2 ? PR + PQ) ?
? PB = (PQ ? PR ? ?2) / (PR + PQ) ? PB = (9 ? 12 ? ?2) / (12 + 9) = 36 ? ?2 / 7
MB = MQ ? BQ, devemos então determinar BQ aplicando o teorema dos cossenos no triângulo BPQ:
BQ2= PB2 + PQ2 ? 2 ? PB ? PQ ? cos (P)
BQ2= (36 ? ?2 / 7)2 + 92 ? 2 ? (36 ? ?2 / 7) ? 9 ? cos (45°) =
= 2592 / 49 + 81 ? (648 ? ?2 / 7) ? (?2 / 2) = 2592 / 49 + 81 ? 648 / 7 = 2025 / 49
BQ2= 2025 / 49 ? BQ = ?(2025 / 49) = 45 / 7
Calculando MB:
MQ = RM = PM = 15 / 2
MB = MQ ? BQ = (15 / 2) ? (45 / 7) = 15 / 14.
Resolução a pedido da Profª. Édnamar.
- Questão 21 E 22 ? Vestibulinho Etec ? 2° Semestre De 2.014
Considere as informações para responder às questões de números 21 e 22. Um técnico em móveis projetou uma estante conforme a figura 1. A figura 2 apresenta o esquema da parte frontal da estante. No esquema da figura 2, tem-se que: D é ponto...
- Triângulo Retângulo
Todo triângulo que tem um ângulo de 90°(ângulo reto) é denominado triângulo retângulo. O triângulo ABC tem um ângulo reto e é denominado triângulo retângulo: Onde: a: hipotenusa; b e c: catetos; h: altura relativa à hipotenusa; m e n: projeções...
- Razões Trigonométricas
Trigonometria I TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO Em princípio, Trigonometria é o estudo da relações entre as medidas de ângulos e lados nos triângulos retângulos (trigono = triângulo e metria = medida). 1. RAZÕES TRIGONOMÉTRICAS O triângulo...
- Razões Trigonométricas
Trigonometria I TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO Em princípio, Trigonometria é o estudo da relações entre as medidas de ângulos e lados nos triângulos retângulos (trigono = triângulo e metria = medida). 1. RAZÕES TRIGONOMÉTRICAS O triângulo...
- Teorema Da Bissetriz Interna
Este é um importante teorema da geometria plana, onde conseguimos determinar segmentos proporcionais em um triângulo. Mas o que é bissetriz? Definição: Bissetriz é o lugar geométrico dos pontos equidistantes de duas retas, concorrentes dividindo...
Matemática
Questão 55 ? Processo de Promoção ? Professor de Matemática ? SEE ? São Paulo ? 2.013
O triângulo PQR da figura é retângulo em P. O segmento PM é mediana relativa ao lado RQ do triângulo e PB é bissetriz do ângulo P. A medida do cateto PR é 12 cm e a medida do cateto PQ é 9 cm

A distância entre os pontos M e B é igual a
(A) 30 / 7.
(B) 45 / 27.
(C) 15 / 14.
(D) 5 / 4.
(E) 13 / 12.
Solução: (C)
Antes de resolver gostaria de pedir desculpas, pois tenho a incrível capacidade de sempre escolher o caminho mais longo na resolução.
A medida da mediana relativa a hipotenusa de um triangulo retângulo é igual a metade da medida da hipotenusa.
h2 = c2 + c2 ? RQ2 = PR2 + PQ2 ? RQ2= 122 + 92 = 225 ?RQ = ?225 = 15
A medida de PM = RQ / 2 = 15 / 2.
Para determinar a medida da bissetriz PB inicialmente traçamos por B o segmento BA paralelo a um dos catetos, neste caso utilizamos o cateto PQ (vide, Fig. 1). O triângulo RAB é semelhante ao triângulo RPQ, portanto:
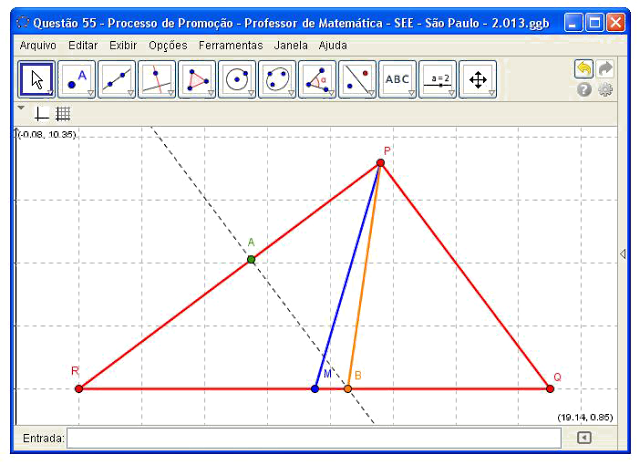 |
| Figura 1: Construção auxiliar. |
PA2+ BA2 = PB2
PA = BA = PB / ?2 = PB ? ?2 / 2
RA = PR ? PA
Sendo o triângulo RAB e o triângulo RPQ semelhantes, temos a seguinte relação:
PQ / BA = PR / RA ? PQ / BA = PR / (PR ? PA)
Resolvemos obtemos:
PQ ? (PR ? PA) = PR ? BA ? PR ? BA = PQ ? PR ? PQ ? PA ?
? PR ? (PB ? ?2 / 2) = PQ ? PR ? PQ ? (PB ? ?2 / 2) ?
? PR ? (PB ? ?2 / 2) + PQ ? (PB ? ?2 / 2) = PQ ? PR ?
? PB ? (?2 / 2) ? (PR + PQ) ? = PQ ? PR ? PB ? (?2 / 2) = (PQ ? PR) / (PR + PQ) ?
? PB = (2 ? PQ ? PR) / (?2 ? PR + PQ) ?
? PB = (PQ ? PR ? ?2) / (PR + PQ) ? PB = (9 ? 12 ? ?2) / (12 + 9) = 36 ? ?2 / 7
MB = MQ ? BQ, devemos então determinar BQ aplicando o teorema dos cossenos no triângulo BPQ:
BQ2= PB2 + PQ2 ? 2 ? PB ? PQ ? cos (P)
BQ2= (36 ? ?2 / 7)2 + 92 ? 2 ? (36 ? ?2 / 7) ? 9 ? cos (45°) =
= 2592 / 49 + 81 ? (648 ? ?2 / 7) ? (?2 / 2) = 2592 / 49 + 81 ? 648 / 7 = 2025 / 49
BQ2= 2025 / 49 ? BQ = ?(2025 / 49) = 45 / 7
Calculando MB:
MQ = RM = PM = 15 / 2
MB = MQ ? BQ = (15 / 2) ? (45 / 7) = 15 / 14.
***
O amigo Raimundo do fórum Pir2 utilizou o teorema da bissetriz interna: uma bissetriz interna de um triângulo divide o lado oposto em segmentos proporcionais aos lados adjacentes.
RB = RQ ? BQ = 15 ? BQ
Aplicando o teorema da bissetriz interna:
PR / RB = PQ / BQ
12 / (15 ? BQ) = 9 / BQ ? 12 ? BQ = 9 ? (15 ? BQ) ?
? 12 ? BQ = 135 ? 9 ? BQ ? 21 ? BQ = 135 ? BQ = 45 / 7
MB = MR ? BQ = (15 / 2) ? (45 / 7) = 15 / 14.
Referência: DOLCE, Osvaldo. POMPEO, José Niciolau. Fundamentos da Matemática Elementar - Volume 9: Geometria Plana. 7º edição. São Paulo: Editora Atual, 1.997.
Resolução a pedido da Profª. Édnamar.
- Questão 21 E 22 ? Vestibulinho Etec ? 2° Semestre De 2.014
Considere as informações para responder às questões de números 21 e 22. Um técnico em móveis projetou uma estante conforme a figura 1. A figura 2 apresenta o esquema da parte frontal da estante. No esquema da figura 2, tem-se que: D é ponto...
- Triângulo Retângulo
Todo triângulo que tem um ângulo de 90°(ângulo reto) é denominado triângulo retângulo. O triângulo ABC tem um ângulo reto e é denominado triângulo retângulo: Onde: a: hipotenusa; b e c: catetos; h: altura relativa à hipotenusa; m e n: projeções...
- Razões Trigonométricas
Trigonometria I TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO Em princípio, Trigonometria é o estudo da relações entre as medidas de ângulos e lados nos triângulos retângulos (trigono = triângulo e metria = medida). 1. RAZÕES TRIGONOMÉTRICAS O triângulo...
- Razões Trigonométricas
Trigonometria I TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO Em princípio, Trigonometria é o estudo da relações entre as medidas de ângulos e lados nos triângulos retângulos (trigono = triângulo e metria = medida). 1. RAZÕES TRIGONOMÉTRICAS O triângulo...
- Teorema Da Bissetriz Interna
Este é um importante teorema da geometria plana, onde conseguimos determinar segmentos proporcionais em um triângulo. Mas o que é bissetriz? Definição: Bissetriz é o lugar geométrico dos pontos equidistantes de duas retas, concorrentes dividindo...
