Matemática
Relações de Girard
Considere a função polinomial
F(x) = a0. xn + a1. xn – 1 + a2. xn – 2 +... + an – 1. x + an, sendo a0 ≠ 0 e n ≥ 1.
Considerando o teorema da decomposição podemos representar F(x) = a0 . (x – r1) . (x – r2) . ... . (x – rn).
Empregando a propriedade distributiva, tornando redutíveis os termos semelhantes, e ordenando o polinômio, temos:
F(x) = a0 . xn – a0(r1 + r2 + ... + rn) . xn-1 + a0 (r1r2 + r1r3 + ...) xn-2 + ...
Se igualarmos os coeficientes deste último polinômio, dois a dois, respectivamente, como os coeficientes iniciais a0, a1, a2, ..., an, obtemos n relações entre as raízes e os coeficientes de F, tais relações são denominadas Relações de Girard, e são as seguintes:

Relações de Girard para uma equação de grau 2
A equação a0x2 + a1 x + a2 = 0 possue como raízes os termos r1 e r2, nesse caso:
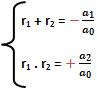
Relações de Girard para uma equação de grau 3
A equação a0x3 + a1x2 + a2x + a3 = 0 possui como raízes os termos r1, r2 e r3, nesse caso:
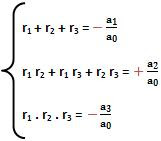
Relações de Girard para uma equação de grau 4
A equação a0x4 + a1x3 + a2x2 + a3x + a4 = 0 possui como raízes os termos r1, r2, r3 e r4, nesse caso:
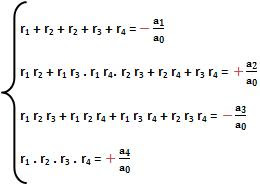
extraido de www.colegioweb.com.br
- Polinômios
I - Polinômios 1 - Definição: Seja C o conjunto dos números complexos ( números da forma a + bi , onde a e b são números reais e i é a unidade imaginária tal que i2 = -1) . Entende-se por polinômio em C à função: P(x) = aoxn + a1xn-1 + a2xn-2...
- Equações Polinomiais
Seja "p(x)" o polinômio dado por: p(x) = an . xn + an–1 . xn–1 + an–2 . xn–2 + . . . + a2 . x2 + a1 . x + a0. Os elementos ai são chamados de coeficientes. (...
- Relações De Girard
As fundamentações de Girard são responsáveis pela relação existente entre os coeficientes de uma equação algébrica e suas raízes. Na equação do 2º grau, as relações são obtidas por meio das fórmulas da soma e do produto: – b/a e c/a,...
- Relações De Girard
Relações de GirardMarcos Noé Raízes de equações do 2º grauAlbert Girard aprofundou, aproximadamente no ano de 1629, os estudos sobre as raízes de equações do 2º grau criando relações entre os coeficientes a, b e c....
- Polinômios
I - Polinômios 1 - Definição: Seja C o conjunto dos números complexos ( números da forma a + bi , onde a e b são números reais e i é a unidade imaginária tal que i2 = -1) . Entende-se por polinômio em C à função: P(x) = aoxn + a1xn-1 + a2xn-2...
Matemática
Relação de Girard
Relações de Girard
Considere a função polinomial
F(x) = a0. xn + a1. xn – 1 + a2. xn – 2 +... + an – 1. x + an, sendo a0 ≠ 0 e n ≥ 1.
Considerando o teorema da decomposição podemos representar F(x) = a0 . (x – r1) . (x – r2) . ... . (x – rn).
Empregando a propriedade distributiva, tornando redutíveis os termos semelhantes, e ordenando o polinômio, temos:
F(x) = a0 . xn – a0(r1 + r2 + ... + rn) . xn-1 + a0 (r1r2 + r1r3 + ...) xn-2 + ...
Se igualarmos os coeficientes deste último polinômio, dois a dois, respectivamente, como os coeficientes iniciais a0, a1, a2, ..., an, obtemos n relações entre as raízes e os coeficientes de F, tais relações são denominadas Relações de Girard, e são as seguintes:

Relações de Girard para uma equação de grau 2
A equação a0x2 + a1 x + a2 = 0 possue como raízes os termos r1 e r2, nesse caso:
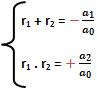
Relações de Girard para uma equação de grau 3
A equação a0x3 + a1x2 + a2x + a3 = 0 possui como raízes os termos r1, r2 e r3, nesse caso:
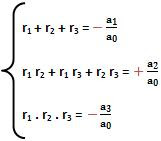
Relações de Girard para uma equação de grau 4
A equação a0x4 + a1x3 + a2x2 + a3x + a4 = 0 possui como raízes os termos r1, r2, r3 e r4, nesse caso:
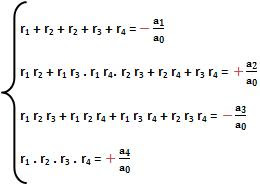
extraido de www.colegioweb.com.br
- Polinômios
I - Polinômios 1 - Definição: Seja C o conjunto dos números complexos ( números da forma a + bi , onde a e b são números reais e i é a unidade imaginária tal que i2 = -1) . Entende-se por polinômio em C à função: P(x) = aoxn + a1xn-1 + a2xn-2...
- Equações Polinomiais
Seja "p(x)" o polinômio dado por: p(x) = an . xn + an–1 . xn–1 + an–2 . xn–2 + . . . + a2 . x2 + a1 . x + a0. Os elementos ai são chamados de coeficientes. (...
- Relações De Girard
As fundamentações de Girard são responsáveis pela relação existente entre os coeficientes de uma equação algébrica e suas raízes. Na equação do 2º grau, as relações são obtidas por meio das fórmulas da soma e do produto: – b/a e c/a,...
- Relações De Girard
Relações de GirardMarcos Noé Raízes de equações do 2º grauAlbert Girard aprofundou, aproximadamente no ano de 1629, os estudos sobre as raízes de equações do 2º grau criando relações entre os coeficientes a, b e c....
- Polinômios
I - Polinômios 1 - Definição: Seja C o conjunto dos números complexos ( números da forma a + bi , onde a e b são números reais e i é a unidade imaginária tal que i2 = -1) . Entende-se por polinômio em C à função: P(x) = aoxn + a1xn-1 + a2xn-2...
