Matemática
Nesta postagem, veremos que:
\begin{equation*}
\int \frac{x}{ax+b}dx = \frac{1}{a^2} \left(ax -b \ln \left|ax+b \right| \right)+C
\end{equation*}
onde $a$ e $b$ são constantes $\in \mathbb{R}$, sendo $a \neq 0$.
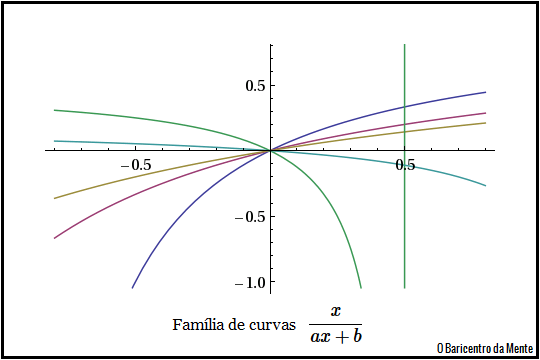
Seja a integral:
\begin{equation*}
I = \int \frac{x}{ax+b} dx
\end{equation*}
Reescrevemos o integrando como:
\begin{equation*}
I = \int \left(\frac{1}{a}-\frac{b}{a(ax+b)}\right) dx
\end{equation*}
Integrando termo a termo:
\begin{equation*}
I = \frac{1}{a} \int dx - \frac{b}{a} \int \frac{1}{ax+b} dx
\end{equation*}
Para o integrando $\cfrac{1}{ax+b}$, fazemos a substituição $u = ax+b$. Assim, $du = a~dx$ e $dx = \cfrac{1}{a}du$:
\begin{equation*}
I = \frac{1}{a} \int dx - \frac{b}{a} \int \frac{1}{u}\cdot \frac{1}{a} du \\
\ \\
I = \frac{1}{a} \int dx - \frac{b}{a^2} \int \frac{1}{u} du
\end{equation*}
A integral de $1$ é $x$ e a integral de $\cfrac{1}{u}$ é $\ln (u)$. Assim:
\begin{equation*}
I = \frac{x}{a} - \frac{b}{a^2} \ln (u)+C \\
\ \\
I = \frac{ax - b \ln (u)}{a^2} + C\\
\ \\
I = \frac{1}{a^2}\left( ax-b \ln (u)\right)+C
\end{equation*}
Mas $u = ax+b$, assim:
\begin{equation}
I = \frac{1}{a^2} \left(ax - b \ln |ax+b|\right) + C
\end{equation}
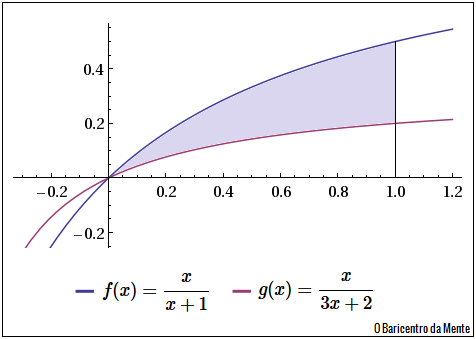
A área desejada é a diferença entre as áreas das duas curvas. Para o cálculo dessas área, utilizamos o conceito de integral definida com limite inferior igual a $0$ e superior igual a $1$, de modo que:
\begin{equation*}
A = \int_0^1 \frac{x}{x+1}dx - \int_0^1 \frac{x}{3x+2}dx
\end{equation*}
Utilizamos a fórmula obtida em $(1)$.
\begin{equation*}
A = \left[ \left(x - \ln |x+1|\right) \right]_0^1 - \left[ \frac{1}{9} \left(3x - 2 \ln |3x+2|\right)\right]_0^1\\
\ \\
A = \left[ 1- \ln (2) + \ln (1)\right] - \left[ \frac{3-2\ln(5)+2\ln(2)}{9}\right]\\
\ \\
A \approx 0,177~\text{unidades de área}
\end{equation*}
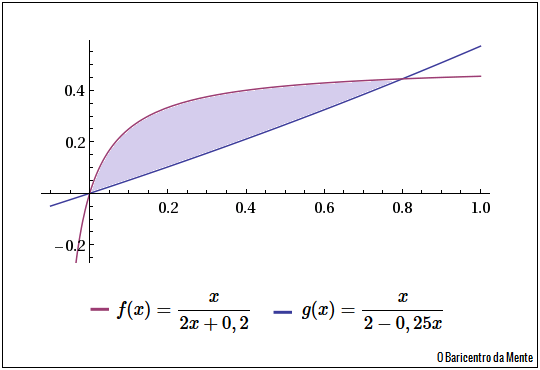
Começamos escrevendo as funções como:
\begin{equation*}
f(x) = \frac{5x}{10x+1} \quad \text{e} \quad g(x) = \frac{4x}{8-x}
\end{equation*}
Para encontrarmos os ponto de intersecção entre as duas curvas, fazemos $f(x)=g(x)$ e calculamos o valor de $x$:
\begin{equation*}
\frac{5x}{10x+1} = \frac{4x}{8-x}\\
\ \\
5x(8-x) = 4x(10x+1)\\
\ \\
45x^2-36x = 0\\
\ \\
x(45x-36)=0\\
\ \\
x_1=0 \quad \text{e} \quad x_2 = \cfrac{4}{5}
\end{equation*}
Desta forma, os limites de integração serão $0$ e $4/5$, e a área desejada será a diferença das áreas de $f(x)$ e $g(x)$, dada pela diferença das integrais definidas:
\begin{equation*}
A = \int_0^{4/5}\frac{x}{2x+\frac{1}{5}}dx - \int_0^{4/5}\frac{x}{2-\frac{x}{4}} dx
\end{equation*}
Para a primeira integral, temos que $a=2$ e $b=1/5$. Para a segunda integral, temos $a=-1/4$ e $b=2$. Assim, aplicando a fórmula encontrada em $(1)$:
\begin{equation*}
A = \left[ \frac{1}{4}\left(2x-\frac{1}{5}\ln\left|2x+\frac{1}{5}\right| \right) \right]_0^{4/5} - \left[16\left( -\frac{x}{4}-2\ln \left|-\frac{x}{4}+2\right|\right)\right]_0^{4/5}
\end{equation*}
Aplicando os limites em $x$:
\begin{equation*}
A=\left[ \frac{1}{4}\left( \frac{8}{5}-\frac{1}{5}\ln\left(\frac{9}{5}\right) \right) -\frac{1}{4}\left( -\frac{1}{5}\ln\left(\frac{1}{5}\right) \right) \right] - \\
\ \\
\left[ 16\left( -\frac{1}{5}-2\ln\left(\frac{9}{5}\right) \right) - 16\left( -2\ln(2) \right) \right]
\ \\
A \approx 0,1186 ~\text {unidades de área}
\end{equation*}
Integração por substituição
Integração por partes

- Resolução Da Integral $\displaystyle \int \frac{x^2+1}{x^2-1}dx$
Nesta postagem, veremos que: \begin{equation*} \int \frac{x^2+1}{x^2-1}dx = x+ \ln|x-1|- \ln|x+1| + C \end{equation*} onde $x \in \mathbb{R}$, sendo $x \neq \pm 1$. Seja a integral: \begin{equation*} I = \int \frac{x^2+1}{x^2-1}dx \end{equation*} Decompomos...
- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a^2}dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a^2}\ dx = \frac{1}{a}\text{arctg}\left(\frac{x}{a}\right) + C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2 + a^2 \neq 0$. Seja a integral:...
- Resolução Da Integral $\displaystyle \int \text{sen}^2 (ax)dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \text{sen}^2(ax)dx = \frac{x}{2} - \frac{\text{sen}(2ax)}{4a} + C \end{equation*} onde $a \in \mathbb{R}$ e $a \neq 0$. Seja a integral: \begin{equation*} I = \int \text{sen}^2(ax)dx \end{equation*}...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
Matemática
Resolução da integral $\small \displaystyle \int \frac{x}{ax+b} dx$
Nesta postagem, veremos que:
\begin{equation*}
\int \frac{x}{ax+b}dx = \frac{1}{a^2} \left(ax -b \ln \left|ax+b \right| \right)+C
\end{equation*}
onde $a$ e $b$ são constantes $\in \mathbb{R}$, sendo $a \neq 0$.

Seja a integral:
\begin{equation*}
I = \int \frac{x}{ax+b} dx
\end{equation*}
Reescrevemos o integrando como:
\begin{equation*}
I = \int \left(\frac{1}{a}-\frac{b}{a(ax+b)}\right) dx
\end{equation*}
Integrando termo a termo:
\begin{equation*}
I = \frac{1}{a} \int dx - \frac{b}{a} \int \frac{1}{ax+b} dx
\end{equation*}
Para o integrando $\cfrac{1}{ax+b}$, fazemos a substituição $u = ax+b$. Assim, $du = a~dx$ e $dx = \cfrac{1}{a}du$:
\begin{equation*}
I = \frac{1}{a} \int dx - \frac{b}{a} \int \frac{1}{u}\cdot \frac{1}{a} du \\
\ \\
I = \frac{1}{a} \int dx - \frac{b}{a^2} \int \frac{1}{u} du
\end{equation*}
A integral de $1$ é $x$ e a integral de $\cfrac{1}{u}$ é $\ln (u)$. Assim:
\begin{equation*}
I = \frac{x}{a} - \frac{b}{a^2} \ln (u)+C \\
\ \\
I = \frac{ax - b \ln (u)}{a^2} + C\\
\ \\
I = \frac{1}{a^2}\left( ax-b \ln (u)\right)+C
\end{equation*}
Mas $u = ax+b$, assim:
\begin{equation}
I = \frac{1}{a^2} \left(ax - b \ln |ax+b|\right) + C
\end{equation}
Exemplo $1$:
Encontrar a área entre as curvas $f(x)= \cfrac{x}{x+1}$ e $g(x)=\cfrac{x}{3x+2}$, compreendida no intervalo $[0,1]$.
A área desejada é a diferença entre as áreas das duas curvas. Para o cálculo dessas área, utilizamos o conceito de integral definida com limite inferior igual a $0$ e superior igual a $1$, de modo que:
\begin{equation*}
A = \int_0^1 \frac{x}{x+1}dx - \int_0^1 \frac{x}{3x+2}dx
\end{equation*}
Utilizamos a fórmula obtida em $(1)$.
\begin{equation*}
A = \left[ \left(x - \ln |x+1|\right) \right]_0^1 - \left[ \frac{1}{9} \left(3x - 2 \ln |3x+2|\right)\right]_0^1\\
\ \\
A = \left[ 1- \ln (2) + \ln (1)\right] - \left[ \frac{3-2\ln(5)+2\ln(2)}{9}\right]\\
\ \\
A \approx 0,177~\text{unidades de área}
\end{equation*}
Exemplo $2$:
Encontrar a área compreendida entre as curvas $f(x)=\cfrac{x}{2x+0,2}$ e $g(x)=\cfrac{x}{2-0,25 x}$, sendo o limite inferior igual a $0$ e o limite superior o ponto de intersecção entre as duas curvas no quadrante onde $x$ e $y$ são positivos.
Começamos escrevendo as funções como:
\begin{equation*}
f(x) = \frac{5x}{10x+1} \quad \text{e} \quad g(x) = \frac{4x}{8-x}
\end{equation*}
Para encontrarmos os ponto de intersecção entre as duas curvas, fazemos $f(x)=g(x)$ e calculamos o valor de $x$:
\begin{equation*}
\frac{5x}{10x+1} = \frac{4x}{8-x}\\
\ \\
5x(8-x) = 4x(10x+1)\\
\ \\
45x^2-36x = 0\\
\ \\
x(45x-36)=0\\
\ \\
x_1=0 \quad \text{e} \quad x_2 = \cfrac{4}{5}
\end{equation*}
Desta forma, os limites de integração serão $0$ e $4/5$, e a área desejada será a diferença das áreas de $f(x)$ e $g(x)$, dada pela diferença das integrais definidas:
\begin{equation*}
A = \int_0^{4/5}\frac{x}{2x+\frac{1}{5}}dx - \int_0^{4/5}\frac{x}{2-\frac{x}{4}} dx
\end{equation*}
Para a primeira integral, temos que $a=2$ e $b=1/5$. Para a segunda integral, temos $a=-1/4$ e $b=2$. Assim, aplicando a fórmula encontrada em $(1)$:
\begin{equation*}
A = \left[ \frac{1}{4}\left(2x-\frac{1}{5}\ln\left|2x+\frac{1}{5}\right| \right) \right]_0^{4/5} - \left[16\left( -\frac{x}{4}-2\ln \left|-\frac{x}{4}+2\right|\right)\right]_0^{4/5}
\end{equation*}
Aplicando os limites em $x$:
\begin{equation*}
A=\left[ \frac{1}{4}\left( \frac{8}{5}-\frac{1}{5}\ln\left(\frac{9}{5}\right) \right) -\frac{1}{4}\left( -\frac{1}{5}\ln\left(\frac{1}{5}\right) \right) \right] - \\
\ \\
\left[ 16\left( -\frac{1}{5}-2\ln\left(\frac{9}{5}\right) \right) - 16\left( -2\ln(2) \right) \right]
\ \\
A \approx 0,1186 ~\text {unidades de área}
\end{equation*}
Veja mais:
Lista de resolução de integraisIntegração por substituição
Integração por partes

- Resolução Da Integral $\displaystyle \int \frac{x^2+1}{x^2-1}dx$
Nesta postagem, veremos que: \begin{equation*} \int \frac{x^2+1}{x^2-1}dx = x+ \ln|x-1|- \ln|x+1| + C \end{equation*} onde $x \in \mathbb{R}$, sendo $x \neq \pm 1$. Seja a integral: \begin{equation*} I = \int \frac{x^2+1}{x^2-1}dx \end{equation*} Decompomos...
- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a^2}dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a^2}\ dx = \frac{1}{a}\text{arctg}\left(\frac{x}{a}\right) + C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2 + a^2 \neq 0$. Seja a integral:...
- Resolução Da Integral $\displaystyle \int \text{sen}^2 (ax)dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \text{sen}^2(ax)dx = \frac{x}{2} - \frac{\text{sen}(2ax)}{4a} + C \end{equation*} onde $a \in \mathbb{R}$ e $a \neq 0$. Seja a integral: \begin{equation*} I = \int \text{sen}^2(ax)dx \end{equation*}...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
