Matemática

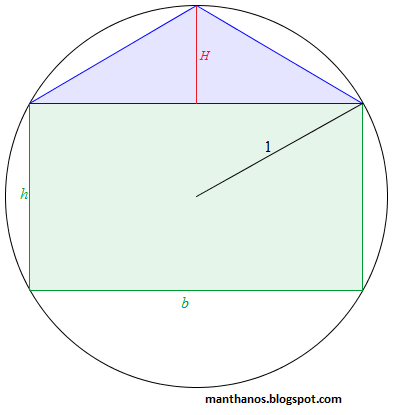
Resolvendo o problema do retângulo e triângulo inscritos

[veja o problema aqui]

Vamos chamar a altura do triângulo de H, conforme a figura abaixo:

Note agora que um modo alternativo de enunciar o problema seria este: encontre h que satisfaça a seguinte igualdade:

${\color{DarkGreen} b}\cdot {\color{DarkGreen} h}=\frac{{\color{DarkGreen} b}\cdot {\color{Red} H}}{2}$

(área do retângulo = área do triângulo)

Dividindo ambos os lados da equação por b, e depois multiplicando ambos os lados por 2 obtemos:

${\color{Red} H }= 2\cdot {\color{DarkGreen} h}$

Dando outra olhada na figura não é difícil perceber que:

${\color{Red} H} + \frac{{\color{DarkGreen} h}}{2}=1$

Nesta última igualdade, podemos subtrair h/2 de ambos os lados para obter:

${\color{Red} H} = 1 - \frac{{\color{DarkGreen} h}}{2}$

Temos então duas expressões diferentes que designam a mesma medida H. Já que são ambas iguais a H são, também, iguais entre si, logo podemos escrever:

$2\cdot {\color{DarkGreen} h} = 1 - \frac{{\color{DarkGreen} h}}{2}$

Resolvendo esta equação obtemos, enfim, o valor de h. Podemos multiplicar ambos os lados por 2 para "eliminar" a fração:

$4\cdot {\color{DarkGreen} h} = 2 - {\color{DarkGreen} h}$

Somando h a ambos os lados:

$4\cdot {\color{DarkGreen} h}+{\color{DarkGreen} h} = 2$

Colocando h em evidência:

$\left (4 + 1 \right )\cdot {\color{DarkGreen} h} = 2$

Efetuando a adição:

$5\cdot {\color{DarkGreen} h} = 2$

Dividindo ambos os lados por 5:

${\color{DarkGreen} h} = \frac{2}{5}$

Efetuando a divisão:

${\color{DarkGreen} h} = 0,4$

E o problema está resolvido!

Observe que tínhamos, inicialmente, 2 valores desconhecidos: a altura do retângulo (h) e a altura do triângulo (H). O que fizemos foi encontrar duas expressões distintas que relacionam estas duas incógnitas - e esta era, justamente, a parte difícil do problema! Feito isso fica fácil de resolver: basta obter algum valor em uma das expressões e substituir na outra (este é um dos mais básicos princípios que se utiliza quando a intenção é solucionar um sistema de equações lineares de duas incógnitas - daí a importâcia de problemas como este).

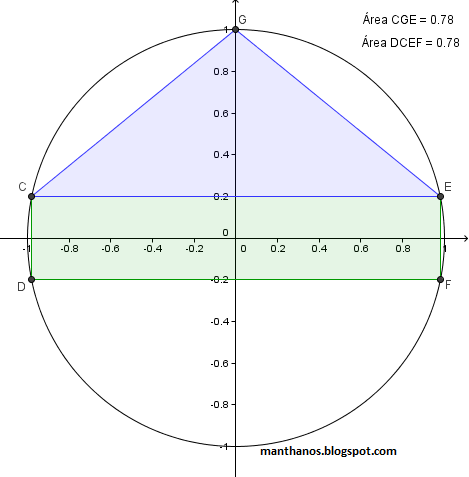
Observe que o Geogebra confirma o resultado acima encontrado:

Referência: solucionado por Diego Monteiro Resende de Andrade.

Relate erros aqui.

- Provando Que Dois Segmentos Desiguais São Iguais!!!
Seja ABC um determinado triângulo e tracemos um segmento de reta PQqualquer paralelo ao segmento de reta AB (vide Figura 1). Figura 1: Construção Inicial. O triângulo ABC é semelhante ao triângulo APQ, pois sabemos que quando traçamos um segmento...

- Jura? 2 é Igual A 1???
Estranho isso hein??? Vamos verificar: Sejam a e b pertencentes ao reais, sendo a e b diferentes de zero. Suponhamos que a = b Então, se a=b, multiplicando os dois lados da igualdade por a temos: a2 = ab Subtraindo b2 dos dois lados da igualdade...

- Área Do Triângulo Equilátero
A área de um triângulo pode ser determinada através da aplicação da seguinte fórmula: Para aplicá-la é preciso ter o valor da base e da altura de um triângulo, sendo assim, uma fórmula de fácil utilização quando o triângulo for retângulo....

- Área Do Retângulo
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com ...

- Triângulo Equilátero
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com...

Matemática