Matemática

Sobre o Produto Escalar

Por: Prof. Paulo Sérgio, Blog Fatos Matemáticos

O Produto Escalar dos vetores $[;\vec{u}= (u_1,u_2,u_3);]$ e $[;\vec{v}=(v_1,v_2,v_3);]$ , denotado por $[;\vec{u}\cdot \vec{v};]$ é definido por:

$[;\vec{u}\cdot \vec{v} = u_1v_1 + u_2v_2 + u_3v_3 \quad \quad (1);]$

Segue desta definição que $[;\vec{u}\cdot {v} = \vec{v}\cdot \vec{u};]$ . Além disso, se $[;\theta;]$ é o ângulo entre dois vetores $[;\vec{u};]$ e $[;\vec{v};]$ , então através da Lei dos Cossenos é fácil mostrar que:

$[;\vec{u}\cdot \vec{v} = |\vec{u}|\cdot |\vec{v}|\cos \theta;]$ com $[;0 \leq \theta \leq \pi;]$ rad [;(2);]

Vejamos agora como podemos relacionar o produto escalar com o módulo de um vetor. Para ver isso, suponhamos que $[;\vec{u} = \vec{v};]$ na definição acima. Assim,

$[;\vec{u}\cdot \vec{u} = u_{1}^2 + u_{2}^2 + u_{3}^2 = |\vec{u}|^2;]$ [;(3);]

Onde segue que o módulo de um vetor é igual a raíz quadrada do produto escalar deste vetor por ele mesmo.

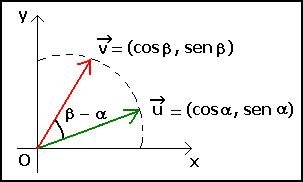
Vejamos uma aplicação elementar do produto escalar que é deduzir a seguinte fórmula trigonométrica:

$[;\cos(\beta - \alpha) = \cos \beta cos \alpha + \sin \beta \sin \alpha;]$

Na notação acima, $[;\vec{u} = (\cos \alpha,\ \sin \alpha);]$ e $[;\vec{v} = (\cos \beta, \ \sin \beta);]$ e pela propriedade [;(3);]

é fácil ver que esses vetores são unitários. Assim, por [;(1);]

, temos:

$[;\vec{u}\cdot \vec{v} = \cos \alpha \cos \beta + \sin \alpha \sin \beta;]$ [;(4);]

e pela fórmula [;(2);]

$[;\vec{u}\cdot \vec{v} = cos(\beta - \alpha);]$ [;(5);]

segue o resultado. Usando o fato que cosseno é uma função par, que o seno é uma função ímpar e que o cosseno do complementar de um ângulo é igual ao seno desse ângulo e vice-versa, obtém-se as demais identidades trigonométricas.

Existem outras aplicações importantes relacionada com o produto escalar, tais como o cálculo do trabalho de uma força constante e em problemas que aparece o vetor projeção.

- ...::definição De Função Do 1º Grau E Zero De Uma Função Do 1º Grau::...
                                FUNÇÃO DO 1º GRAU Prof. Esp. Deivison da Silva e Silvae-mail:[email protected]...

- A Lei Dos Cossenos Através Da Regra De Cramer
       Fonte: Blog Fatos Matemáticos. (http://fatosmatematicos.blogspot.com)As vezes a relação entre assuntos de áreas distintas da Matemática nos surpreende muito.       ...

- Vetores
Fonte: Site Baricentro da Mente. (http://obaricentrodamente.blogspot.com)       Em Física, algumas grandezas necessitam definir o sentido e a direção. Estas grandezas são chamadas de Vetores, dentre elas o deslocamento, velocidade,...

- Cálculo Vetorial
1 - O VETORConsidere o segmento orientado AB na figura abaixo. Observe que o segmento orientado AB é caracterizado por três aspectos bastante definidos: comprimento (denominado módulo)direçãosentido (de A para B)Chama-se vetor ao conjunto infinito...

- Cálculo De Autovalores E Autovetores
Seja A a matriz da transformação T:V → V. A matriz A deve ser, portanto, uma matriz quadrada (n x n). Conforme já visto, para um autovalor λ e um autovetor v, T(v) = λ v. De outra forma, A v = λ v  #A.1#Considerando I a matriz unitária...

Matemática