Matemática
Seja A a matriz da transformação T:V → V. A matriz A deve ser, portanto, uma matriz quadrada (n x n). Conforme já visto, para um autovalor λ e um autovetor v,
Considerando I a matriz unitária (ou matriz identidade), pode-se escrever
Seja a função:
Ela é denominada função característica da matriz A.
Para solução não nula de #B.1#, deve-se ter o determinante nulo:
Resolvendo a equação acima, obtém-se os valores de λ que, substituídos em #A.1#, permitem a determinação dos autovetores.
Exemplo: são dados:
• matriz 3x3 A, para a qual se deseja calcular os autovalores.
• λ I, que é o produto do escalar λ pela matriz unitária I 3x3.
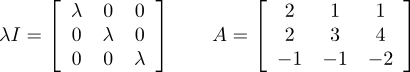
A matriz da diferença λ I − A é

O seu determinante é calculado pelas relações a seguir.
det (λ I − A) = (λ − 2) [ (λ − 3) (λ + 2) − (1) (−4) ] − (−1) [ (−2) (λ + 2) − (1) (−4) ] + (−1) [ (−2) (1) − (1) (λ − 3) ].
det (λ I − A) = [ (λ − 2) (λ − 3) (λ + 2) + 4λ − 8 ] + [−2λ ] − [−λ − 1].
det (λ I − A) = (λ − 2) (λ − 3) (λ + 2) + 3 (λ − 3).
det (λ I − A) = (λ − 3) [ (λ − 2) (λ + 2) + 3 ].
det (λ I − A) = (λ − 3) [ λ2 − 4 + 3 ] = (λ − 3) [ λ2 − 1 ].
Expandindo o último termo e igualando a zero conforme #D.1#,
As soluções dessa equação do terceiro grau são claramente:
Aplica-se agora a igualdade #A.1# para o valor de λ = 1.

Essa relação matricial pode ser transformada em um sistema de equações lineares através do desenvolvimento do produto das matrizes e posterior simplificação.
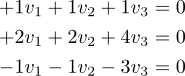
Somando a primeira com a terceira equação, v3 = 0. Substituindo nas demais, chega-se ao resultado
Ou
Há infinitas soluções e pode-se dizer que o vetor é dado por v = α (1, −1, 0) onde α é um escalar não nulo qualquer. Portanto, para o autovalor λ = 1, os autovetores são da forma:
Procedimento idêntico pode ser usado para os demais valores de λ.
fonte:http://www.mspc.eng.br/mam
- Matriz Inversa
Para que uma matriz tenha a sua inversa ela deve ser primeiramente quadrada, ou seja, deve ter o mesmo número de linhas e de colunas. Mas é importante ressaltar que nem todas as matrizes quadradas possuem inversas, nesse caso essas matrizes são chamadas...
- Matriz
1 - Definições: 1.1 - Chama-se Menor Complementar ( D ij ) de um elemento aij de uma matriz quadrada A, ao determinante que se obtém eliminando-se a linha i e a coluna j da matriz. Assim, dada a matriz quadrada de terceira ordem (3x3) A a seguir :...
- Determinantes
Se A é uma matriz quadrada A de ordem 2, dada por: a11 a12 a21 a22 definimos o determinante desta matriz A, denotado por det(A), como: det(A) = a11.a22 - a21.a12 Se A é uma matriz quadrada A de ordem 3, dada por: a11 a12 a13 a21 a22 a23 a31 a32 a33...
- Determinantes
Se A é uma matriz quadrada A de ordem 2, dada por: a11 a12 a21 a22 definimos o determinante desta matriz A, denotado por det(A), como: det(A) = a11.a22 - a21.a12 Se A é uma matriz quadrada A de ordem 3, dada por: a11 a12 a13 a21 a22 a23 a31 a32 a33...
- Cálculo Do Determinante De Uma Matriz Quadrada
Cálculo do determinante de uma matriz quadradaMarcelo Rigonatto Matriz quadradaMatriz quadrada é uma matriz que apresenta o número de linhas e colunas iguais. A toda matriz quadrada está associado um número que recebe a denominação...
Matemática
Cálculo de autovalores e autovetores
Seja A a matriz da transformação T:V → V. A matriz A deve ser, portanto, uma matriz quadrada (n x n). Conforme já visto, para um autovalor λ e um autovetor v,
T(v) = λ v. De outra forma,A v = λ v #A.1#Considerando I a matriz unitária (ou matriz identidade), pode-se escrever
λ v = λ I v. Substituindo na anterior e reagrupando,λ I v − A v = 0. De outra forma,(λ I − A) v = 0 #B.1#Seja a função:
f(λ) = det (λ I − A) #C.1#Ela é denominada função característica da matriz A.
Para solução não nula de #B.1#, deve-se ter o determinante nulo:
det (λ I − A) = 0 #D.1#Resolvendo a equação acima, obtém-se os valores de λ que, substituídos em #A.1#, permitem a determinação dos autovetores.
Exemplo: são dados:
• matriz 3x3 A, para a qual se deseja calcular os autovalores.
• λ I, que é o produto do escalar λ pela matriz unitária I 3x3.
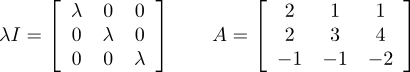
A matriz da diferença λ I − A é

O seu determinante é calculado pelas relações a seguir.
det (λ I − A) = (λ − 2) [ (λ − 3) (λ + 2) − (1) (−4) ] − (−1) [ (−2) (λ + 2) − (1) (−4) ] + (−1) [ (−2) (1) − (1) (λ − 3) ].
det (λ I − A) = [ (λ − 2) (λ − 3) (λ + 2) + 4λ − 8 ] + [−2λ ] − [−λ − 1].
det (λ I − A) = (λ − 2) (λ − 3) (λ + 2) + 3 (λ − 3).
det (λ I − A) = (λ − 3) [ (λ − 2) (λ + 2) + 3 ].
det (λ I − A) = (λ − 3) [ λ2 − 4 + 3 ] = (λ − 3) [ λ2 − 1 ].
Expandindo o último termo e igualando a zero conforme #D.1#,
det (λ I − A) = (λ − 3) (λ + 1) (λ − 1) = 0.As soluções dessa equação do terceiro grau são claramente:
λ = 1
λ = −1
λ = 3
Aplica-se agora a igualdade #A.1# para o valor de λ = 1.

Essa relação matricial pode ser transformada em um sistema de equações lineares através do desenvolvimento do produto das matrizes e posterior simplificação.
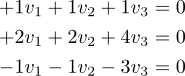
Somando a primeira com a terceira equação, v3 = 0. Substituindo nas demais, chega-se ao resultado
v1 + v2 = 0Ou
v1 = − v2Há infinitas soluções e pode-se dizer que o vetor é dado por v = α (1, −1, 0) onde α é um escalar não nulo qualquer. Portanto, para o autovalor λ = 1, os autovetores são da forma:
α (1, −1, 0) com α ≠ 0.Procedimento idêntico pode ser usado para os demais valores de λ.
fonte:http://www.mspc.eng.br/mam
- Matriz Inversa
Para que uma matriz tenha a sua inversa ela deve ser primeiramente quadrada, ou seja, deve ter o mesmo número de linhas e de colunas. Mas é importante ressaltar que nem todas as matrizes quadradas possuem inversas, nesse caso essas matrizes são chamadas...
- Matriz
1 - Definições: 1.1 - Chama-se Menor Complementar ( D ij ) de um elemento aij de uma matriz quadrada A, ao determinante que se obtém eliminando-se a linha i e a coluna j da matriz. Assim, dada a matriz quadrada de terceira ordem (3x3) A a seguir :...
- Determinantes
Se A é uma matriz quadrada A de ordem 2, dada por: a11 a12 a21 a22 definimos o determinante desta matriz A, denotado por det(A), como: det(A) = a11.a22 - a21.a12 Se A é uma matriz quadrada A de ordem 3, dada por: a11 a12 a13 a21 a22 a23 a31 a32 a33...
- Determinantes
Se A é uma matriz quadrada A de ordem 2, dada por: a11 a12 a21 a22 definimos o determinante desta matriz A, denotado por det(A), como: det(A) = a11.a22 - a21.a12 Se A é uma matriz quadrada A de ordem 3, dada por: a11 a12 a13 a21 a22 a23 a31 a32 a33...
- Cálculo Do Determinante De Uma Matriz Quadrada
Cálculo do determinante de uma matriz quadradaMarcelo Rigonatto Matriz quadradaMatriz quadrada é uma matriz que apresenta o número de linhas e colunas iguais. A toda matriz quadrada está associado um número que recebe a denominação...
