Matemática

Matriz quadrada é uma matriz que apresenta o número de linhas e colunas iguais. A toda matriz quadrada está associado um número que recebe a denominação de determinante. Os determinantes apresentam aplicações na resolução de sistemas lineares e no cálculo da área de um triângulo no plano cartesiano, quando são conhecidas as coordenadas de seus vértices.
Veremos como se dá o cálculo do determinante de matrizes quadradas de 1ª, 2ª e 3ª ordem.
Determinante de uma matriz de 1ª ordem.
Dada uma matriz quadrada de 1ª ordem M = [a11], seu determinante será o número a11. Ou seja:
det M = a11
Determinante de uma matriz de 2ª ordem.
Dada uma matriz quadrada de 2ª ordem, seu determinante será obtido fazendo a diferença entre o produto dos elementos da diagonal principal e o produto dos elementos da diagonal secundária. Ou seja:
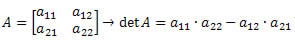
Determinante de uma matriz de 3ª ordem.
Para calcular o determinante de uma matriz quadrada de ordem 3 utilizamos o método de Sarrus. Observe como se dá esse processo:
Considere a matriz quadrada de 3ª ordem a seguir:

O método de Sarrus consiste em:
1º: Repetir as duas primeiras colunas da matriz ao lado da última coluna.

2º: Somar o produto dos elementos da diagonal principal com o produto dos elementos das duas diagonais paralelas à principal.

(a11∙a22∙a33+a12∙a23∙a31+a13∙a21∙a32 )
3º: Somar o produto dos elementos da diagonal secundária com o produto dos elementos das duas diagonais paralelas à secundária:

(a12∙a21∙a33 + a11∙a23∙a32 + a13∙a22∙a31)
4º: O determinante será a diferença entre os resultados obtidos nos passos 2 e 3, ou seja:
det A = (a11∙a22∙a33 + a12∙a23∙a31 + a13∙a21∙a32 ) - (a12∙a21∙a33 + a11∙a23∙a32 + a13∙a22∙a31)
Vejamos alguns exemplos de aplicação.
Exemplo 1. Calcule o determinante da matriz abaixo:
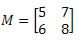
Solução: A matriz M é quadrada de ordem 2 x 2. Assim, seu determinante será dado por:
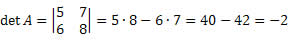
Exemplo 2. Calcule o determinante da matriz
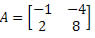
Solução:
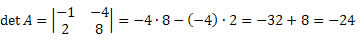
Exemplo 3. Dada a matriz M3 x 3 abaixo, calcule seu determinante.
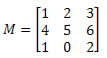
Solução:
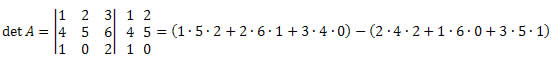
det A = (10+12+0) - (16+0+15)=22-31 = -9
Exemplo 4. Calcule o determinante da matriz 3 x 3 abaixo:
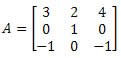
Solução:
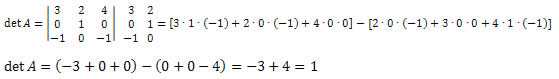
- Matriz
1 - Definições: 1.1 - Chama-se Menor Complementar ( D ij ) de um elemento aij de uma matriz quadrada A, ao determinante que se obtém eliminando-se a linha i e a coluna j da matriz. Assim, dada a matriz quadrada de terceira ordem (3x3) A a seguir :...
- Matriz Triangular
Uma matriz constitui uma ferramenta matemática utilizada em diversas situações relacionadas à Informática e Engenharia. Elas são formadas por elementos distribuídos em linhas e colunas (aij), onde i: linhas e j: colunas. As matrizes possuem inúmeras...
- Determinantes
Se A é uma matriz quadrada A de ordem 2, dada por: a11 a12 a21 a22 definimos o determinante desta matriz A, denotado por det(A), como: det(A) = a11.a22 - a21.a12 Se A é uma matriz quadrada A de ordem 3, dada por: a11 a12 a13 a21 a22 a23 a31 a32 a33...
- Determinante De Uma Matriz Quadrada De Ordem N
Para conhecermos o determinante de uma matriz de ordem 2x2 e 3x3 utilizamos a Regra de Sarrus. Nos casos em que a ordem for maior que 3x3 devemos utilizar o Teorema de Laplace. Enfatizaremos nosso estudo dos determinantes nas matrizes de ordem 2x2 e 3x3...
- Regra De Sarrus
Regra de SarrusMarcos Noé Regra de SarrusA Regra de Sarrus é utilizada no cálculo de determinantes de matrizes quadradas. Sua aplicação permite o cálculo de maneira prática, relacionando a diagonal principal com a diagonal...
Matemática
Cálculo do determinante de uma matriz quadrada
Cálculo do determinante de uma matriz quadrada
Marcelo Rigonatto
Matriz quadrada
Veremos como se dá o cálculo do determinante de matrizes quadradas de 1ª, 2ª e 3ª ordem.
Determinante de uma matriz de 1ª ordem.
Dada uma matriz quadrada de 1ª ordem M = [a11], seu determinante será o número a11. Ou seja:
det M = a11
Determinante de uma matriz de 2ª ordem.
Dada uma matriz quadrada de 2ª ordem, seu determinante será obtido fazendo a diferença entre o produto dos elementos da diagonal principal e o produto dos elementos da diagonal secundária. Ou seja:
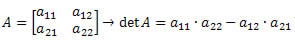
Determinante de uma matriz de 3ª ordem.
Para calcular o determinante de uma matriz quadrada de ordem 3 utilizamos o método de Sarrus. Observe como se dá esse processo:
Considere a matriz quadrada de 3ª ordem a seguir:

O método de Sarrus consiste em:
1º: Repetir as duas primeiras colunas da matriz ao lado da última coluna.

2º: Somar o produto dos elementos da diagonal principal com o produto dos elementos das duas diagonais paralelas à principal.

(a11∙a22∙a33+a12∙a23∙a31+a13∙a21∙a32 )
3º: Somar o produto dos elementos da diagonal secundária com o produto dos elementos das duas diagonais paralelas à secundária:

(a12∙a21∙a33 + a11∙a23∙a32 + a13∙a22∙a31)
4º: O determinante será a diferença entre os resultados obtidos nos passos 2 e 3, ou seja:
det A = (a11∙a22∙a33 + a12∙a23∙a31 + a13∙a21∙a32 ) - (a12∙a21∙a33 + a11∙a23∙a32 + a13∙a22∙a31)
Vejamos alguns exemplos de aplicação.
Exemplo 1. Calcule o determinante da matriz abaixo:
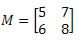
Solução: A matriz M é quadrada de ordem 2 x 2. Assim, seu determinante será dado por:
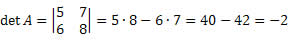
Exemplo 2. Calcule o determinante da matriz
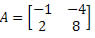
Solução:
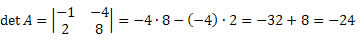
Exemplo 3. Dada a matriz M3 x 3 abaixo, calcule seu determinante.
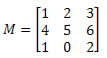
Solução:
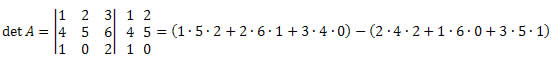
det A = (10+12+0) - (16+0+15)=22-31 = -9
Exemplo 4. Calcule o determinante da matriz 3 x 3 abaixo:
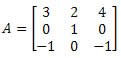
Solução:
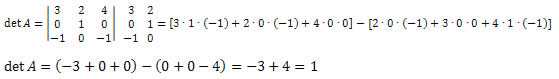
- Matriz
1 - Definições: 1.1 - Chama-se Menor Complementar ( D ij ) de um elemento aij de uma matriz quadrada A, ao determinante que se obtém eliminando-se a linha i e a coluna j da matriz. Assim, dada a matriz quadrada de terceira ordem (3x3) A a seguir :...
- Matriz Triangular
Uma matriz constitui uma ferramenta matemática utilizada em diversas situações relacionadas à Informática e Engenharia. Elas são formadas por elementos distribuídos em linhas e colunas (aij), onde i: linhas e j: colunas. As matrizes possuem inúmeras...
- Determinantes
Se A é uma matriz quadrada A de ordem 2, dada por: a11 a12 a21 a22 definimos o determinante desta matriz A, denotado por det(A), como: det(A) = a11.a22 - a21.a12 Se A é uma matriz quadrada A de ordem 3, dada por: a11 a12 a13 a21 a22 a23 a31 a32 a33...
- Determinante De Uma Matriz Quadrada De Ordem N
Para conhecermos o determinante de uma matriz de ordem 2x2 e 3x3 utilizamos a Regra de Sarrus. Nos casos em que a ordem for maior que 3x3 devemos utilizar o Teorema de Laplace. Enfatizaremos nosso estudo dos determinantes nas matrizes de ordem 2x2 e 3x3...
- Regra De Sarrus
Regra de SarrusMarcos Noé Regra de SarrusA Regra de Sarrus é utilizada no cálculo de determinantes de matrizes quadradas. Sua aplicação permite o cálculo de maneira prática, relacionando a diagonal principal com a diagonal...
