Matemática
A conjectura dos números primos gêmeos afirma que existem infinitos números primos gêmeos, mas até hoje tal afirmação ainda não foi provada. Matemáticos acreditam que esta conjectura é verdadeira, baseado apenas nas evidências numéricas e raciocínios heurísticos envolvendo a distribuição probabilística dos números primos.
Em $1919$, Brun mostrou que a série formada pela soma dos recíprocos dos primos gêmeos converge para uma soma chamada constante de Brun $(0,6601618158 \cdots)$ em sua homenagem.
Em janeiro de $2007$, o projeto computacional sobre a distribuição dos números primos gêmeos (Twin Prime Search and Prime Grid) encontrou os maiores primos gêmeos contendo $58.771$ dígitos:
\begin{equation*}
2.003.663.613 \times 2^{195.000} \pm 1
\end{equation*}
Em julho de 2009, foram encontrados primos gêmeos ainda maiores, com 100.355 dígitos:
\begin{equation*}
65.516468355 \times 2^{333.333} \pm 1
\end{equation*}
Dados dois primos gêmeos $x$ e $y$, escritos sob a forma $x = 6n + 1$ e $y = 6n – 1$ para $n$ natural.
Assim:
\begin{equation*}
x^2 - y^2 = (6n+1)^2 - (6n-1)^2\\
x^2 - y^2 = 36n^2 + 12n + 1 - 36n^2 +12n -1\\
x^2 - y^2 = 24n
\end{equation*}
Por exemplo, podemos montar uma tabela e verificar os resultados:
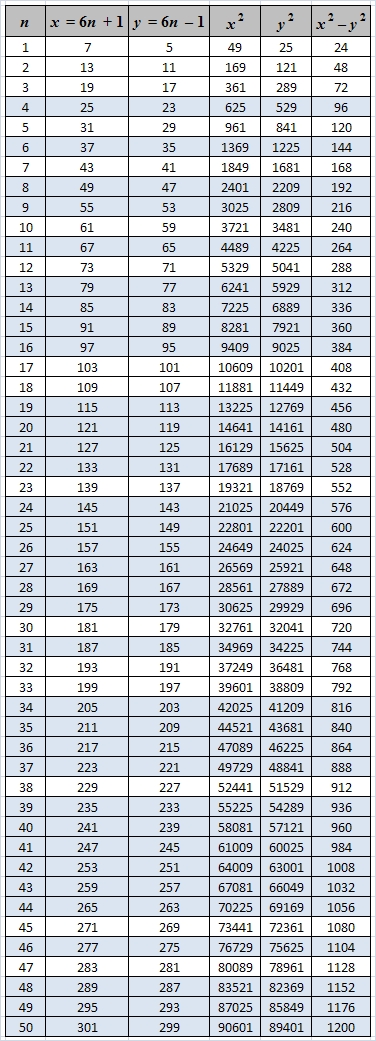
Observando a tabela acima, podemos notar que, apesar de encontrarmos pares gêmeos, nem para todo n natural encontramos primos gêmeos do tipo $6n \pm 1$.
\begin{equation*}
3, 5, 7, 11, 13, 17, 19, 29, 31, 41, 43, 59, 61, 71, 73, 101, 103, 107, 109, 137, 139, 149, 151, 179, 181, 191, 193, 197, 199, 227, 229, 239, 241, 269, 271, 281, 283, 311, 313, 347, 349, 419, 421, 431, 433, 461, 463, 521, 523, 569, 571, 599, 601, 617, 619, 641, 643,\cdots
\end{equation*}
\begin{equation*}
(x-y)(x+y) = 24n\\
2(x+y) = 24n\\
x+y = 12
\end{equation*}
donde segue o resultado.
Note que uma terna de primos contém um par de primos gêmeos da forma $(p,p+2)$ ou $(p+4, p+6)$. Vejamos uma pequena tabela com cada um dos tipos:
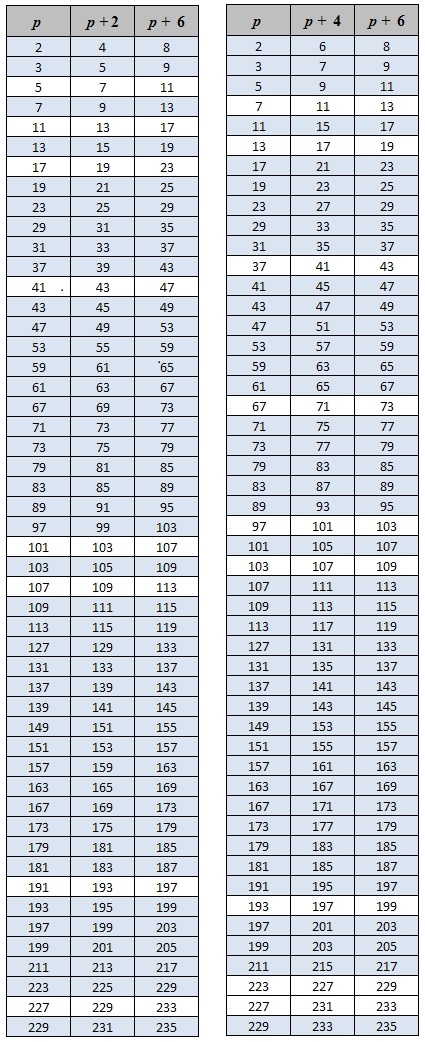Temos as seguintes primeiras ternas:
\begin{equation*}
(5, 7, 11), (7, 11, 13), (11, 13, 17), (13, 17, 19), (37, 41, 43), (41, 43, 47), (67, 71, 73), (97, 101, 103), (101, 103, 107), (103, 107, 109), (107, 109, 113), (191, 193, 197), 193, 197, 199), (223, 227, 229), (227, 229, 233), (227, 231, 233), \cdots
\end{equation*}
A Série dos Recíprocos dos Números Primos no blog Fatos Matemáticos
Teoremas Interessantes Sobre Números Primos no blog Fato Matemáticos
A Demonstração de Euclides Sobre a Existência de Infinitos Números Primos
- Ex-sanduicheiro Do Subway Impressiona Com Descoberta Matemática
Um completo desconhecido no mundo da matemática fez uma descoberta revolucionária que ajudará a entender melhor os números.Basicamente, um cara que uma vez se esforçou para encontrar um emprego e teve que trabalhar na rede fast food Subway está...
- Curiosidades Dos Números Primos
Os números primos tem algumas propriedades muito curiosas e interessantes. A seguir, vejam algumas delas: 2 é o único primo par; Não há número primo algum que termine em 5, exceto o próprio 5; Todos os números primos diferentes de 2, 3, 5, 7...
- Prova Do Teorema De Pitágoras, Baseado Nas Relações Métricas Da Circunferência
Esta demonstração do teorema de Pitágoras, baseia-se nas relações métricas da circunferência. Considere o triângulo $ABC$. Tomando como centro o ponto $B$ e raio igual a hipotenusa $AB$, traçamos uma circunferência. A seguir prolongamos os...
- Conjecturas De Sebá Sobre A Distância Entre Dois Números Primos Consecutivos
Depois que Euclides provou, usando a matemática de sua época, que existem infinitos números primos, outros matemáticos também demonstraram, mas usando uma matemática muito mais avançada daquela que Euclides usou na sua demonstração.Que existem...
- A Demonstração De Euclides Sobre A Existência De Infinitos Números Primos
O grande matemático Húngaro George Pólya $(1887 – 1985)$, recomendava um jeito divertido de se habituar aos fundamentos da matemática e de passar o tempo numa sala de espera de aeroporto ou de consultório médico: relembrar uma prova matemática...
Matemática
Sobre os Primos Gêmeos
A conjectura dos números primos gêmeos afirma que existem infinitos números primos gêmeos, mas até hoje tal afirmação ainda não foi provada. Matemáticos acreditam que esta conjectura é verdadeira, baseado apenas nas evidências numéricas e raciocínios heurísticos envolvendo a distribuição probabilística dos números primos.
Em $1919$, Brun mostrou que a série formada pela soma dos recíprocos dos primos gêmeos converge para uma soma chamada constante de Brun $(0,6601618158 \cdots)$ em sua homenagem.
Em janeiro de $2007$, o projeto computacional sobre a distribuição dos números primos gêmeos (Twin Prime Search and Prime Grid) encontrou os maiores primos gêmeos contendo $58.771$ dígitos:
\begin{equation*}
2.003.663.613 \times 2^{195.000} \pm 1
\end{equation*}
Em julho de 2009, foram encontrados primos gêmeos ainda maiores, com 100.355 dígitos:
\begin{equation*}
65.516468355 \times 2^{333.333} \pm 1
\end{equation*}
Definição $1$:
Um par de números primos $x$ e $y$ com $x > y$ é chamado de primos gêmeos se $x = y + 2$.Teorema de Sebá $1$:
Se $x$ e $y$ são dois primos gêmeos maiores que três sob a forma $6n \pm 1$, então, temos que $x^2 – y^2$ é divisível por $24$, para todo $x > y$.Demonstração:
Dados dois primos gêmeos $x$ e $y$, escritos sob a forma $x = 6n + 1$ e $y = 6n – 1$ para $n$ natural.
Assim:
\begin{equation*}
x^2 - y^2 = (6n+1)^2 - (6n-1)^2\\
x^2 - y^2 = 36n^2 + 12n + 1 - 36n^2 +12n -1\\
x^2 - y^2 = 24n
\end{equation*}
Por exemplo, podemos montar uma tabela e verificar os resultados:
Observando a tabela acima, podemos notar que, apesar de encontrarmos pares gêmeos, nem para todo n natural encontramos primos gêmeos do tipo $6n \pm 1$.
\begin{equation*}
3, 5, 7, 11, 13, 17, 19, 29, 31, 41, 43, 59, 61, 71, 73, 101, 103, 107, 109, 137, 139, 149, 151, 179, 181, 191, 193, 197, 199, 227, 229, 239, 241, 269, 271, 281, 283, 311, 313, 347, 349, 419, 421, 431, 433, 461, 463, 521, 523, 569, 571, 599, 601, 617, 619, 641, 643,\cdots
\end{equation*}
Corolário $1$:
A soma de dois primos gêmeos maiores que três é divisível por $12$.Demonstração:
Dados dois primos gêmeos $x$ e $y$ com $x – y = 2$. Pelo teorema anterior $x^2 – y^2 = 24n$, sendo n natural não nulo. Assim,\begin{equation*}
(x-y)(x+y) = 24n\\
2(x+y) = 24n\\
x+y = 12
\end{equation*}
donde segue o resultado.
Definição $2$:
Uma terna de primos é uma terna da forma $(p, p+2, p+6)$ ou $(p, p+4, p+6)$. Com exceção trivial das ternas $(2,3,5)$ e $(3,5,7)$.Note que uma terna de primos contém um par de primos gêmeos da forma $(p,p+2)$ ou $(p+4, p+6)$. Vejamos uma pequena tabela com cada um dos tipos:
\begin{equation*}
(5, 7, 11), (7, 11, 13), (11, 13, 17), (13, 17, 19), (37, 41, 43), (41, 43, 47), (67, 71, 73), (97, 101, 103), (101, 103, 107), (103, 107, 109), (107, 109, 113), (191, 193, 197), 193, 197, 199), (223, 227, 229), (227, 229, 233), (227, 231, 233), \cdots
\end{equation*}
Veja mais:
Quantos Números Primos Existem?A Série dos Recíprocos dos Números Primos no blog Fatos Matemáticos
Teoremas Interessantes Sobre Números Primos no blog Fato Matemáticos
A Demonstração de Euclides Sobre a Existência de Infinitos Números Primos
- Ex-sanduicheiro Do Subway Impressiona Com Descoberta Matemática
Um completo desconhecido no mundo da matemática fez uma descoberta revolucionária que ajudará a entender melhor os números.Basicamente, um cara que uma vez se esforçou para encontrar um emprego e teve que trabalhar na rede fast food Subway está...
- Curiosidades Dos Números Primos
Os números primos tem algumas propriedades muito curiosas e interessantes. A seguir, vejam algumas delas: 2 é o único primo par; Não há número primo algum que termine em 5, exceto o próprio 5; Todos os números primos diferentes de 2, 3, 5, 7...
- Prova Do Teorema De Pitágoras, Baseado Nas Relações Métricas Da Circunferência
Esta demonstração do teorema de Pitágoras, baseia-se nas relações métricas da circunferência. Considere o triângulo $ABC$. Tomando como centro o ponto $B$ e raio igual a hipotenusa $AB$, traçamos uma circunferência. A seguir prolongamos os...
- Conjecturas De Sebá Sobre A Distância Entre Dois Números Primos Consecutivos
Depois que Euclides provou, usando a matemática de sua época, que existem infinitos números primos, outros matemáticos também demonstraram, mas usando uma matemática muito mais avançada daquela que Euclides usou na sua demonstração.Que existem...
- A Demonstração De Euclides Sobre A Existência De Infinitos Números Primos
O grande matemático Húngaro George Pólya $(1887 – 1985)$, recomendava um jeito divertido de se habituar aos fundamentos da matemática e de passar o tempo numa sala de espera de aeroporto ou de consultório médico: relembrar uma prova matemática...