Matemática
 Que existem infinitos números primos, não há mais dúvida após a demonstração dada por Euclides, mas e a distância entre dois números primos consecutivos, por que nenhum autor de livros de teoria dos números ainda não se pronunciou? É claro, que à medida que os números primos crescem, a distância entre dois números primos consecutivos cresce enormemente, haja vista que existem desertos de primos, com lacunas preenchidas por números compostos, de comprimentos tão grande quanto se queira,.
Que existem infinitos números primos, não há mais dúvida após a demonstração dada por Euclides, mas e a distância entre dois números primos consecutivos, por que nenhum autor de livros de teoria dos números ainda não se pronunciou? É claro, que à medida que os números primos crescem, a distância entre dois números primos consecutivos cresce enormemente, haja vista que existem desertos de primos, com lacunas preenchidas por números compostos, de comprimentos tão grande quanto se queira,.
Exemplo $1$: $2,3,5,7,11,13,17$
\begin{matrix}
17–2= (3–2)+(5–3)+(7–5)+(11–7)+(13–11)+(17–13)
\\15=1+2+2+4+2+4
\end{matrix}
Exemplo $2$: $31, 37, 41, 43, 47, 53$
\begin{matrix}
53–31=(37–31)+(41–37)+(43–41)+(47–43)+(53–47)
\\22=6+4+2+4+6
\end{matrix}
Exemplo $3$: $127, 131, 137, 139, 149$
\begin{matrix}
149–127=(131–127)+(137–131)+(139–137)+(149–139)
\\22=4+6+2+10
\end{matrix}
Exemplo $4$: $1901, 1907, 1913, 1931$
\begin{matrix}
1931–1901=(1907–1901)+(1913–1907)+(1931–1913)
\\30=6+6+18
\end{matrix}
Exemplo $5$: $2689, 2693, 2699, 2707$
\begin{matrix}
2707-2689=(2693–2689)+(2699–2693)+(2707–2699)
\\18=4+6+8
\end{matrix}
Exemplo $9$: Sejam $p_1$ e $p_n$ dois primos consecutivos $p_1=89$ e $p_n=97$, então $p_n–p_1=8$. Logo $k=8$ e $k–1=8–1=7$. Portanto, existem $7$ números compostos entre os dois primos consecutivos $89$ e $97$.
Tabela $1$: A diferença $\sqrt{p_2}-\sqrt{p_1}$, para $p_2-p_1=2$
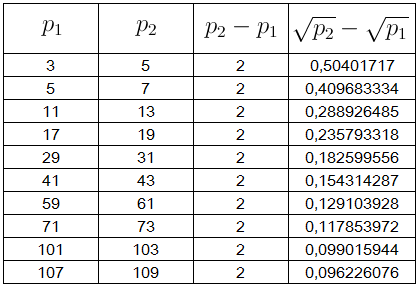
Tabela $2$: A diferença $\sqrt{p_2}-\sqrt{p_1}$, para $p_2-p_1=4$
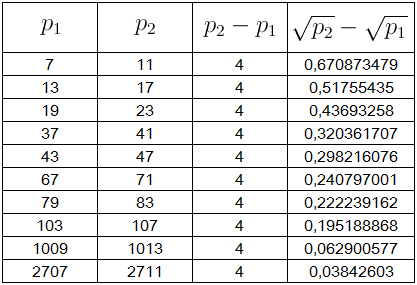
Tabela $3$: A diferença $\sqrt{p_2}-\sqrt{p_1}$, para $p_2-p_1=6$
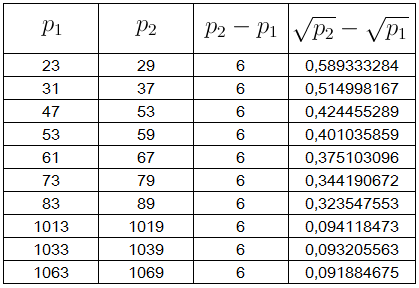
Tabela $4$: A diferença $\sqrt{p_2}-\sqrt{p_1}$, para $p_2-p_1=8$
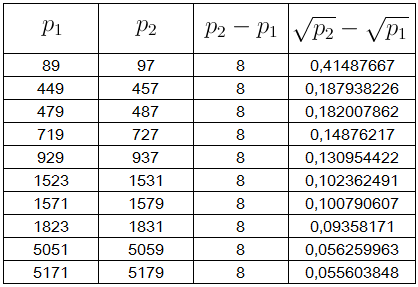
Tabela $5$: A diferença $\sqrt{p_2}-\sqrt{p_1}$, para $p_2-p_1=10$
Veja mais:
Sobre os Primos Gêmeos
Deserto Entre Números Primos
Critérios de Divisibilidade por Qualquer Número Primo Maior que Onze

- "demonstração Por Absurdo"
Olá, gente! Hoje falarei sobre o método de demonstração por redução ao absurdo. A teoria é muito curta e intuitiva, porém a pratica pode ser muito complicada. De forma didática, para demonstrar alguma proposição por absurdo você deve assumir...
- Curiosidades Dos Números Primos
Os números primos tem algumas propriedades muito curiosas e interessantes. A seguir, vejam algumas delas: 2 é o único primo par; Não há número primo algum que termine em 5, exceto o próprio 5; Todos os números primos diferentes de 2, 3, 5, 7...
- O Tijolo De Euler
Por: Sebastião Vieira do Nascimento (Sebá) Este artigo é sobre aplicação de ternos pitagóricos em um dos problemas insolúveis da Matemática. O tijolo de Euler é um paralelepípedo regular de lados que são números inteiros $A$, $B$ e $C$, sendo...
- Sobre Os Primos Gêmeos
A conjectura dos números primos gêmeos afirma que existem infinitos números primos gêmeos, mas até hoje tal afirmação ainda não foi provada. Matemáticos acreditam que esta conjectura é verdadeira, baseado apenas nas evidências numéricas e...
- Quantos Números Primos Existem?
Por: Sebastião Vieira do Nascimento (Sebá) Euclides demonstrou que existem infinitos primos. A demonstração de Euclides é muito simples, se não, vejamos: Suponha, por absurdo, que o número de primos seja finito e sejam p1, p2, p3, ..., pn primos....
Matemática
Conjecturas de Sebá Sobre a Distância Entre Dois Números Primos Consecutivos
Depois que Euclides provou, usando a matemática de sua época, que existem infinitos números primos, outros matemáticos também demonstraram, mas usando uma matemática muito mais avançada daquela que Euclides usou na sua demonstração.
Será que existe algum caso particular no qual os números primos apresentem algum padrão na sua distribuição? Sim! É o que veremos a seguir.
Conjectura (Sebá $1$): Se escolhermos uma sequência de n primos consecutivos $p_1$, $p_2$, $p_3$, $\cdots$, $p_{n-2}$, $p_{n-1}$, $p_n$, e subtrairmos $(p_2 – p_1)$, $(p_3 – p_2)$, $\cdots$ , $(p_{n-1} – p_{n-2})$ e $(p_n – p_{n-1})$, a soma das diferenças é igual a $p_n – p_1$, ou seja, $p_n – p_1 =$ $(p_2 – p_1)$ $+ (p_3 – p_2)$ $+ \cdots + (p_{n-1} – p_{n-2})$ $+ ( p_n – p_{n-1})$.
Exemplo $1$: $2,3,5,7,11,13,17$
\begin{matrix}
17–2= (3–2)+(5–3)+(7–5)+(11–7)+(13–11)+(17–13)
\\15=1+2+2+4+2+4
\end{matrix}
Exemplo $2$: $31, 37, 41, 43, 47, 53$
\begin{matrix}
53–31=(37–31)+(41–37)+(43–41)+(47–43)+(53–47)
\\22=6+4+2+4+6
\end{matrix}
Exemplo $3$: $127, 131, 137, 139, 149$
\begin{matrix}
149–127=(131–127)+(137–131)+(139–137)+(149–139)
\\22=4+6+2+10
\end{matrix}
Exemplo $4$: $1901, 1907, 1913, 1931$
\begin{matrix}
1931–1901=(1907–1901)+(1913–1907)+(1931–1913)
\\30=6+6+18
\end{matrix}
Exemplo $5$: $2689, 2693, 2699, 2707$
\begin{matrix}
2707-2689=(2693–2689)+(2699–2693)+(2707–2699)
\\18=4+6+8
\end{matrix}
E assim por diante.
Por meio dos exemplos da conjectura (Sebá 1), elaborou-se a seguinte conjectura:
Conjectura (Sebá $2$): Se $p_1$ e $p_n$ forem dois primos consecutivos e $p_n–p_1=k$, então $k–1$ é a quantidade de números compostos entre $p_1$ e $p_n$.
Exemplo $6$: Sejam $p_1$ e $p_n$ dois primos consecutivos $p_1=3$ e $p_n=5$, então $p_n–p_1=2$. Logo, $k=2$ e $k–1=2–1=1$. Portanto, existe um número composto entre os dois primos consecutivos $3$ e $5$.
Exemplo $6$: Sejam $p_1$ e $p_n$ dois primos consecutivos $p_1=3$ e $p_n=5$, então $p_n–p_1=2$. Logo, $k=2$ e $k–1=2–1=1$. Portanto, existe um número composto entre os dois primos consecutivos $3$ e $5$.
Exemplo $7$: Sejam $p_1$ e $p_n$ dois primos consecutivos $p_1=7$ e $p_n=11$, então $p_n–p_1=4$. Logo $k=4$ e $k–1=4–1=3$. Portanto, existem $3$ números compostos entre os dois primos consecutivos $7$ e $11$.
Exemplo $8$: Sejam $p_1$ e $p_n$ dois primos consecutivos $p_1=23$ e $p_n=29$, então $p_n–p_1=6$. Logo $k=6$ e $k–1=6–1=5$. Portanto, existem $5$ números compostos entre os dois primos consecutivos $23$ e $29$.
Exemplo $9$: Sejam $p_1$ e $p_n$ dois primos consecutivos $p_1=89$ e $p_n=97$, então $p_n–p_1=8$. Logo $k=8$ e $k–1=8–1=7$. Portanto, existem $7$ números compostos entre os dois primos consecutivos $89$ e $97$.
Exemplo $10$: Sejam $p_1$ e $p_n$ dois primos consecutivos $p_1=139$ e $p_n=149$, então $p_n–p_1=10$. Logo $k=10$ e $k–1=10–1=9$. Portanto, existem $9$ números compostos entre os dois primos consecutivos $139$ e $149$.
Exemplo $11$: Sejam $p_1$ e $p_n$ dois primos consecutivos $p_1=75042769$ e $p_n=75042917$, então $p_n–p_1=148$. Logo $k=148$ e $k–1=148–1=147$. Portanto, existem $147$ números compostos entre os dois primos consecutivos $75042769$ e $75042917$.
E assim por diante.
Já que à medida que os números primos crescem, a distância entre dois números primos consecutivos também cresce. Vamos analisar o comprimento da distância entre dois números primos consecutivos por meio da diferença entre as suas raízes quadradas.
Conjectura (Sebá $3$): Se $p_1$ e $p_2$ forem dois primos consecutivos e $p_2-p_1=2n$ então as diferenças $\sqrt{p_2}-\sqrt{p_1}$ decrescem à medida que $p_1$ e $p_2$ crescem.
Tabela $1$: A diferença $\sqrt{p_2}-\sqrt{p_1}$, para $p_2-p_1=2$

Tabela $2$: A diferença $\sqrt{p_2}-\sqrt{p_1}$, para $p_2-p_1=4$

Tabela $3$: A diferença $\sqrt{p_2}-\sqrt{p_1}$, para $p_2-p_1=6$

Tabela $4$: A diferença $\sqrt{p_2}-\sqrt{p_1}$, para $p_2-p_1=8$

Tabela $5$: A diferença $\sqrt{p_2}-\sqrt{p_1}$, para $p_2-p_1=10$

E assim por diante.
Nota-se pelas tabelas acima que para $p_2-p_1=2$, $4$, $6$, $8$ ou $10$, as diferenças $\sqrt{p_2}-\sqrt{p_1}$ decrescem à medida que $p_1$ e $p_2$
Será que a diferença $\sqrt{p_2}-\sqrt{p_1}$ é menor que a unidade porque as diferenças $2$, $4$, $6$, $8$ ou $10$ são pequenas entre os dois primos consecutivos $p_1$ e $p_2$? Tendo em vista que à medida que os números primos crescem eles vão ficando mais escassos, será que se aumentarmos $p_1$ e $p_2$ para a ordem de centenas de milhares ou milhões, as diferenças $\sqrt{p_2}-\sqrt{p_1}$ continuarão menores que a unidade? É o que veremos a seguir.
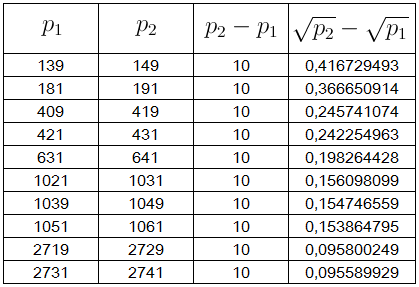
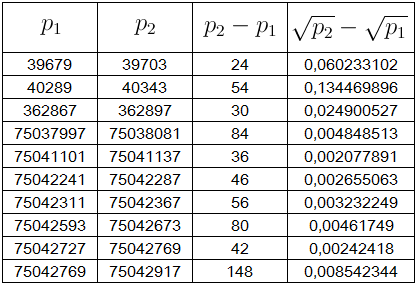
Tabela $6$: A diferença $\sqrt{p_2}-\sqrt{p_1}$, para $22 \leq p_2 - p_1 \leq 148$

Para a tabela $6$, nota-se que para $p_1$ e$ p_2$ na ordem de milhões, as diferenças $\sqrt{p_2}-\sqrt{p_1}$ ainda continuam menores que $0,5$.
Conjectura (Sebá $4$): Se $p_1$ e $p_2$ forem dois números primos consecutivos, então $\sqrt{p_2}-\sqrt{p_1}<1$.
Qual será o comportamento da diferença $\sqrt{p_2}-\sqrt{p1}$ se $p_1$ e $p_2$ nao forem consecutivos? Sempre que $p_2-p_1=2$, $p_1$ e $p_2$ são consecutivos, mas se $p_2-p_1=4$, $6$, $8$, $10$, $\cdots$ $p_1$ e $p_2$ podem ser consecutivos ou não. Se não, vejamos:
Para $p_1 = 3$ e $p_2 = 7$, temos que $p_2 – p_1 = 4$. Assim, $p_1$ e $p_2$ não são consecutivos porque existe o primo $5$ entre os primos $3$ e $7$.
Para $p_1 = 7$ e $p_2 = 11$, temos que $p_2 – p_1 = 4$. Assim, $p_1$ e $p_2$ são consecutivos porque não existe nenhum primo entre os primos $7$ e $11$.
Para $p_1 = 7$ e $p_2 = 13$, temos que $p_2 – p1 = 6$. Assim, $p_1$ e $p_2$ não são consecutivos porque existe o primo $11$ entre os primos $7$ e $13$.
Para $p_1 = 23$ e $p_2 = 29$, temos que $p_2 – p1 = 6$. Assim, $p_1$ e $p_2$ são consecutivos porque não existe nenhum primo entre os primos $23$ e $29$.
Para $p_1 = 11$ e $p_2 = 19$, temos que $p_2 – p1 = 8$. Assim, $p_1$ e $p_2$ não são consecutivos porque existem os primos $13$ e $17$ entre os primos $11$ e $19$.
Para $p_1 = 89$ e $p_2 = 97$, temos que $p_2 – p1 = 8$. Assim, $p_1$ e $p_n$ são consecutivos porque não existe nenhum primo entre os primos $89$ e $97$.
Para $p_1 = 13$ e $p_2 = 23$, temos que $p_2 – p1 = 10$. Assim, $p_1$ e $p_2$ não são consecutivos porque existem os primos $17$ e $19$ entre os primos $13$ e $23$.
.
Para $p_1 = 139$ e $p_2 = 149$, temos que $p_2 – p_1 = 10$. Assim, $p_1$ e $p_2$ são consecutivos porque não existe nenhum primo entre os primos $139$ e $149$.
Vejamos o comportamento da diferença $\sqrt{p_2}-\sqrt{p_1}$ se $p_1$ e $p_2$ não forem consecutivos:
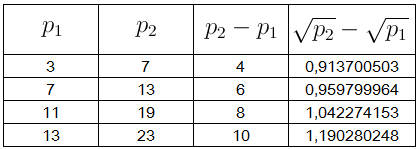
Tabela $7$: A diferença $\sqrt{p_2}-\sqrt{p_1}$ para $p_1$ e $p_2$ não-consecutivos

Nota-se pela tabela $7$ que para $p_2-p_1=4$, $6$, $8$ ou $10$, as diferenças $\sqrt{p_2}-\sqrt{p_1}$ aumentam à medida que $p_1$ e $p_2$ aumentam, chegando a serem próximas ou maiores que a unidade.
Conjectura (Sebá $5$): Se $p_1$ e $p_2$ não forem consecutivos, então $0<\sqrt{p_2}-\sqrt{p_1}<1$ ou $\sqrt{p_2}-\sqrt{p_1}>1$.
Este artigo foi cedido gentilmente por Sebastião Vieira do Nascimento (Sebá). Professor Titular (por concurso) aposentado da UFCG – PB, além de colaborador deste blog.
Veja mais:
Sobre os Primos Gêmeos
Deserto Entre Números Primos
Critérios de Divisibilidade por Qualquer Número Primo Maior que Onze

- "demonstração Por Absurdo"
Olá, gente! Hoje falarei sobre o método de demonstração por redução ao absurdo. A teoria é muito curta e intuitiva, porém a pratica pode ser muito complicada. De forma didática, para demonstrar alguma proposição por absurdo você deve assumir...
- Curiosidades Dos Números Primos
Os números primos tem algumas propriedades muito curiosas e interessantes. A seguir, vejam algumas delas: 2 é o único primo par; Não há número primo algum que termine em 5, exceto o próprio 5; Todos os números primos diferentes de 2, 3, 5, 7...
- O Tijolo De Euler
Por: Sebastião Vieira do Nascimento (Sebá) Este artigo é sobre aplicação de ternos pitagóricos em um dos problemas insolúveis da Matemática. O tijolo de Euler é um paralelepípedo regular de lados que são números inteiros $A$, $B$ e $C$, sendo...
- Sobre Os Primos Gêmeos
A conjectura dos números primos gêmeos afirma que existem infinitos números primos gêmeos, mas até hoje tal afirmação ainda não foi provada. Matemáticos acreditam que esta conjectura é verdadeira, baseado apenas nas evidências numéricas e...
- Quantos Números Primos Existem?
Por: Sebastião Vieira do Nascimento (Sebá) Euclides demonstrou que existem infinitos primos. A demonstração de Euclides é muito simples, se não, vejamos: Suponha, por absurdo, que o número de primos seja finito e sejam p1, p2, p3, ..., pn primos....
