Matemática
Este artigo é sobre aplicação de ternos pitagóricos em um dos problemas insolúveis da Matemática.
O tijolo de Euler é um paralelepípedo regular de lados que são números inteiros $A$, $B$ e $C$, sendo $A > B > C$, cujas diagonais da face $D_{AB}$, $D_{AC}$ e $D_{BC}$ também são números inteiros. Se a diagonal principal é aquela que liga os pontos $M$ e $N$ do paralelepípedo, também for um número inteiro, o tijolo é dito perfeito. No entanto, não se conhece nenhum exemplo de um tijolo perfeito de Euler.
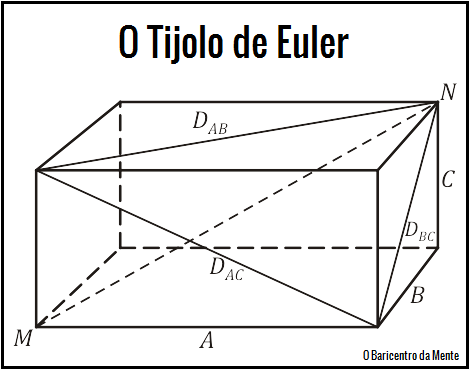
O tijolo simples de Euler imperfeito, com os menores valores para $A$, $B$ e $C$ que se conhece, tem as medidas: $A=240$, $B=117$ e $C=44$. As diagonais são :$D_{AB}=267$, $D_{AC}=244$ e $D_{BC}=125$. Foi descoberto em $1719$ pelo matemático Halcke.
Com o advento dos computadores, ficou muito mais fácil encontrar tijolos de Euler. Ao que parece, já são conhecido os $5.000$ menores tijolos de Euler, medidos pelo maior lado. Os $5$ primeiros são: $(240,117,44)$, $(275, 252,240)$, $(693,480,140)$, $(720,132,85)$ e $(792, 231, 160)$.
O problema matemático relacionado é encontrar uma ou mais fórmulas que produzam todos os tijolos de Euler perfeitos, casos existam. Até hoje, ninguém conseguiu isso.
Como os triângulos $ABD$ e $DBE$ são retângulos e além disso, fazendo coincidir a diagonal da base com um dos catetos da diagonal do paralelepípedo, obtém-se:
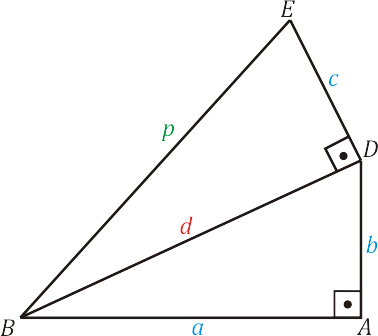
A diagonal $d$ da base é tal que: $d^2 = a^2 + b^2$. Para a diagonal $p$ do paralelepípedo, temos que: $p^2 = c^2 + d^2$. Portanto, a fim de que os lados, a altura e a diagonal da base do paralelepípedo sejam números inteiros, basta que os dois ternos $(b, a, d)$ e $(d,c, p)$ sejam pitagóricos.
Já que a diagonal da base é um dos catetos do triângulo retângulo que forma a diagonal do paralelepípedo, logo as dimensões de cada tijolo e sua diagonal, em números inteiros, são dadas pela quadra $(b,a,c,p)$.
Seja $b$ o lado menor do tijolo. Como o triângulo $ABD$ tem que ser pitagórico, logo $d^2=a^2+b^2$ ou:
\begin{equation}
(d+a) = \frac{b^2}{d-a}
\end{equation}
Uma vez que $a$ e $d$ são inteiros, logo $(d-a)$ tem que dividir $b^2$ sem deixar resto. Logo, $(d-a)$ são os divisores positivos de $b^2$. Seja $b$ um primo ímpar. Os divisores de $b^2$ são: $b^2$ e $1$. Substituindo $b^2$, $b$
e $1$ em $(1)$, obtém-se os seguintes sistemas de equações:
\begin{equation*}
S_1=\left\{\begin{matrix}
d & - & a & = & b^2\\
d & + & a & = & 1
\end{matrix}\right.\\
\ \\
S_2=\left\{\begin{matrix}
d & - & a & = & b\\
d & + & a & = & b
\end{matrix}\right.\\
\ \\
S_3 = \left\{\begin{matrix}
d & - & a & = & 1\\
d & + & a & = & b^2
\end{matrix}\right.
\end{equation*}
Dos três sistemas de equações acima, somente o $S_3$ é compatível. Resolvendo o sistema $S_3$, obtém-se:
\begin{equation}
d=\frac{b^2+1}{2} \quad \text{e} \quad a=d-1
\end{equation}
Já que $p^2 = c^2 + d^2$, então:
\begin{equation}
p+c = \frac{d^2}{p-c}
\end{equation}
Como $b$ é um primo ímpar, logo $d$ pode ser uma primo ímpar ou um número composto ímpar.
Se $d$ for um primo ímpar, então chega-se aos mesmos resultados que se chegou para $b$, ou seja, três sistemas de equações $S_1$, $S_2$ e $S_3$, dos quais somente $S_3$ é compatível. E obtém-se para $p$ e $c$ as seguintes fórmulas:
\begin{equation}
p=\frac{d^2+1}{2} \quad \text{e} \quad c=p-1
\end{equation}
Resposta: Se $b$ e $d$ forem dois primos ímpares, então só existe um tijolo de Euler.
As medidas das diagonais do tijolo de Euler são dadas por:
\begin{equation*}
d=\frac{b^2+1}{2} \quad \text{diagonal da base do tijolo de Euler}\\
\ \\
p = \frac{d^2+1}{2} \quad \text{diagonal }MN\text{ do tijolo de Euler}
\end{equation*}
As dimensões do tijolo de Euler são dadas por:
$\quad a = d-1$ (lado maior)
$\quad b$ = (lado menor)
$\quad c=p-1$ (altura)
Como $d^2 = a^2+b^2$, então:
\begin{equation}
d+a = \frac{b^2}{d-a}
\end{equation}
Se $d-a=m$, então:
\begin{equation}
d+a=\frac{b^2}{m}
\end{equation}
Somando as equações membro a membro, obtém-se:
\begin{equation}
2d = \frac{b^2}{m}+m \quad \text{ou} \quad d=\frac{b^2+m^2}{2m} \quad \text{e} \quad a=d-m
\end{equation}
Suponha que $b$ seja par. Como $2d$ é sempre par, logo, a fim de que a soma $\displaystyle \frac{b^2}{m}+m$ seja par, $\displaystyle \frac{b^2}{m}$ e $m$ têm que ser ambos pares. Então, se $b$ for par, o número de soluções é igual ao número de divisores pares de $b^2$, menores que $b$, ou seja, $m < b$. Portanto, o número de triângulos pitagóricos é igual ao número de vezes em que $m$ (par) $<b$, dividir $b^2$ sem deixar resto.
Se $b$ for um número ímpar composto, então, como $2d$ é sempre par, logo, a fim de que a soma $\displaystyle \frac{b^2}{m}+m$ seja par, $m$ tem que ser ímpar. Então, o número de soluções é igual ao número de divisores de $b^2$ menores que $b^2$, ou seja, $m<b$. Portanto, o número de triângulos pitagóricos é igual ao número de vezes em que $m<b$ dividir $b^2$ sem deixar resto.
Já que $p^2=c^2+d^2$, então:
\begin{equation}
p+c = \frac{d^2}{p-c}
\end{equation}
Se $p-c=k$, então:
\begin{equation}
p+c = \frac{d^2}{k}
\end{equation}
Somando as duas equações membro a membro, obtém-se:
\begin{equation*}
2p = \frac{d^2}{k}+k \quad \text{ou} \quad p=\frac{d^2+k^2}{2k} \quad \text{e}\quad c=p-k
\end{equation*}
Se $d$ for um número par ou um ímpar não-primo, chega-se às mesmas conclusões que se chegou para $b$ par ou ímpar, ou seja, se $d$ for par, o número de triângulos pitagóricos é igual ao número de vezes em que $k$ (par) $< d$, dividir $d^2$ sem deixar resto. Se $d$ for ímpar composto, o número de triângulos pitagóricos é igual ao número de vezes em que $k < d$ dividir $d^2$ sem deixar resto.
As medidas das diagonais do tijolo de Euler são dadas por:
\begin{equation*}
d = \frac{b^2+m}{2} \quad \text{diagonal da base do tijolo de Euler}\\
\ \\
p=\frac{d^2 + k^2}{2k} \quad \text{diagonal }MN \text{ do tijolo de Euler}
\end{equation*}
As medidas das dimensões do tijolo de Euler são dadas por:
$\quad a=d-m$ (lado maior)
$\quad b=$ (lado menor)
$\quad c=p-k$ (altura)
d=\frac{5^2+1}{2}=13
\end{equation*}
Resposta: como $b=5$ e $d=13$ são ambos primos, logo, só existe um tijolo de Euler com o lado menor ou igual a $5cm$.
p=\frac{13^2 + 1}{2}=85
\end{equation*}
a & = & 13-1 & = &12 \ cm\\
b & = & \ & \ & 5\ cm\\
c& = & 85-1& = &84 \ cm
\end{matrix}
p=\sqrt{12^2 + 5^2 + 84^2} = \sqrt{144 + 25 + 7056} = 85
\end{equation*}
Sejam $D_{AB}$, $D_{AC}$ e $D_{BC}$, respectivamente, as diagonais do tijolo de Euler:
\begin{equation*}
D_{AB}=\sqrt{12^2+5^2}=13, \quad D_{AC}=\sqrt{12^2+84^2}=84,85 \quad \text{e} \quad D_{BC}=\sqrt{5^2+84^2}=84,15
\end{equation*}
Portanto, se a $D_{MN}$ for inteira, somente a $D_{AB}$ é inteira, ou seja, somente a diagonal da base do tijolo de Euler é inteira.
d = \frac{7^2+1}{2}=25\ cm
\end{equation*}
Como a diagonal da base do tijolo de Euler é um número composto ímpar, logo, o número de tijolos será igual ao número de vezes em que $m<25$ dividir $25^2$ sem deixar resto. Os divisores de $25^2$ menores que $25$ são: $1$ e $25$. Portanto, existem dois tijolos de Euler com o lado menor igual a $7$.
1^o\text{ tijolo:}\ p_1=\frac{25^2+1}{2\cdot 1}=313\ cm\\
\ \\
2^o \text{tijolo:}\ p_2=\frac{25^2 + 5^2}{2\cdot 5}=65\ cm
\end{equation*}
\begin{matrix}
a & = & d-1 & 25-1 & = & 24 \ cm\\
b & = & \ & \ & \ & 7\ cm\\
c & = & p-k & 313-1& = & 312 \ cm
\end{matrix}Verificação:
\begin{equation*}
p = \sqrt{24^2 + 7^2 + 312^2} = 313 \ cm
\end{equation*}
$2^o$ tijolo:
\begin{matrix}
a & = & d-1 & 25-1 & = & 24 \ cm\\
b & = & \ & \ & \ & 7\ cm\\
c & = & p-k & 65-5& = &60 \ cm
\end{matrix}
Verificação:
\begin{equation*}
p = \sqrt{24^2 + 7^2 + 60^2} = 65\ cm
\end{equation*}
Para o divisor $1$:
\begin{equation*}
p_1=\frac{485^2 + 1}{2} = 117613
\end{equation*}
\begin{matrix}
a & = & d_1 - m & 485-2 & = & 483\\
b & = & \ & \ & \ & 44\\
c & = & p_1 - k & 117613-1& = & 117612
\end{matrix}
Verificação: $\displaystyle p_1 = \sqrt{44^2 + 483^2 + 117612^2}=117612$
Para o divisor $5$:
\begin{equation*}
p_2=\frac{485^2 + 5^2}{2 \times 5} = 23525
\end{equation*}
\begin{matrix}
a & = & \ & \ & 483\\
b & = & \ & \ &44\\
c & = & 23525-5 & = & 23520
\end{matrix}
Verificação: $\displaystyle p_2 = \sqrt{483^2 + 44^2 + 23520^2}=23525$
Para o divisor $25$:
\begin{equation*}
p_3=\frac{485^2 + 25^2}{2 \times 25} =4717
\end{equation*}
\begin{matrix}
a & = & \ & \ & 483\\
b & = & \ & \ &44\\
c & = & 4717-25 & = & 4692
\end{matrix}
Verificação: $\displaystyle p_3 = \sqrt{483^2 + 44^2 + 4692^2}=4717$
Para o divisor $97$:
\begin{equation*}
p_4=\frac{485^2 + 97^2}{2 \times 97} =1261
\end{equation*}
\begin{matrix}
a & = & \ & \ & 483\\
b & = & \ & \ &44\\
c & = & 1261-97 & = & 1164
\end{matrix}
Verificação: $\displaystyle p_4 = \sqrt{483^2 + 44^2 + 1164^2}=1261$
Para: $\displaystyle d_2=\frac{44^2+4^2}{2 \times 4} = 244$, temos que os divisores pares de $244^2$, menores que $\displaystyle \frac{244}{2}$ são: $2,4,8$ e $16$.
Para o divisor $2$:
\begin{equation*}
p_5=\frac{244^2 + 2^2}{2 \times 2} =14885
\end{equation*}
\begin{matrix}
a & = & 244-4 & = & 240\\
b & = & \ & \ &44\\
c & = & 14885-2 & = & 14883
\end{matrix}
Verificação: $\displaystyle p_5 = \sqrt{240^2 + 44^2 + 14883^2}=14885$
Para o divisor $4$:
\begin{equation*}
p_6=\frac{244^2 + 4^2}{2 \times 4} =7444
\end{equation*}
\begin{matrix}
a & = & \ & \ & 240\\
b & = & \ & \ &44\\
c & = & 7444-4 & = & 7440
\end{matrix}
Verificação: $\displaystyle p_6 = \sqrt{240^2 + 44^2 + 7440^2}=7444$
Para o divisor $8$:
\begin{equation*}
p_7=\frac{244^2 + 8^2}{2 \times 8} =3725
\end{equation*}
\begin{matrix}
a & = & \ & \ & 240\\
b & = & \ & \ &44\\
c & = & 3725-8 & = & 3717
\end{matrix}
Verificação: $\displaystyle p_7 = \sqrt{240^2 + 44^2 + 3717^2}=3725$
Para o divisor $16$:
\begin{equation*}
p_8=\frac{244^2 + 16^2}{2 \times 16} =1865,5\\
\end{equation*}
$p_8$ não é inteiro, porque $\displaystyle \frac{d^2}{k}=\frac{244^2}{16}$ é ímpar.
Para: $\displaystyle d_3=\frac{44^2+8^2}{2 \times 8} =125$, temos que os divisores pares de $125^2$, menores que $125$ são: $1,5$ e $25$.
Para o divisor $1$:
\begin{equation*}
p_9=\frac{125^2 +1}{2} =7813
\end{equation*}
\begin{matrix}
a & = & 125-8 & = & 117\\
b & = & \ & \ &44\\
c & = & 7813-1 & = & 7812
\end{matrix}
Verificação: $\displaystyle p_9 = \sqrt{117^2 + 44^2 + 7812^2}=7813$
Para o divisor $5$:
\begin{equation*}
p_{10}=\frac{125^2 +5^2}{2 \times 5} =1565
\end{equation*}
\begin{matrix}
a & = & \ & \ & 117\\
b & = & \ & \ &44\\
c & = & 1565-5 & = & 1560
\end{matrix}
Verificação: $\displaystyle p_{10} = \sqrt{117^2 + 44^2 + 1560^2}=1565$
Para o divisor $25$:
\begin{equation*}
p_{11}=\frac{125^2 +25^2}{2 \times 25} =325
\end{equation*}
\begin{matrix}
a & = & \ & \ & 117\\
b & = & \ & \ &44\\
c & = & 325-25 & = & 300
\end{matrix}
Verificação: $\displaystyle p_{11} = \sqrt{117^2 + 44^2 + 300^2}=325$
Para: $\displaystyle d_4=\frac{44^2+16^2}{2 \times 16} = 68,$
$d_4$ não é inteiro porque $\displaystyle \frac{b^2}{m}=\frac{44^2}{16}$ é ímpar.
Para: $\displaystyle d_5=\frac{44^2+22^2}{2 \times 22} = 55$, temos que os divisores de $55^2$, menores que $55$ são: $1,5,11$ e $25$.
Para o divisor $1$:
\begin{equation*}
p_{12}=\frac{55^2 +1}{2} =1513
\end{equation*}
\begin{matrix}
a & = & 55-22 & = & 33\\
b & = & \ & \ &44\\
c & = & 1513-1 & = & 1512
\end{matrix}
Verificação: $\displaystyle p_{12} = \sqrt{44^2 + 33^2 + 1512^2}=1513$
Para o divisor $5$:
\begin{equation*}
p_{13}=\frac{55^2 +5^2}{2 \times 5} =305
\end{equation*}
\begin{matrix}
a & = & \ & \ & 33\\
b & = & \ & \ &44\\
c & = & 305-5 & = & 300
\end{matrix}
Verificação: $\displaystyle p_{13} = \sqrt{44^2 + 33^2 + 300^2}=305$
Para o divisor $11$:
\begin{equation*}
p_{14}=\frac{55^2 +11^2}{2 \times 11} =143
\end{equation*}
\begin{matrix}
a & = & \ & \ & 33\\
b & = & \ & \ & 44\\
c & = & 143-11 & = & 132
\end{matrix}
Verificação: $\displaystyle p_{14} = \sqrt{44^2 + 33^2 + 132^2}=143$
Para o divisor $25$:
\begin{equation*}
p_{15}=\frac{55^2 +25^2}{2 \times 25} =73
\end{equation*}
\begin{matrix}
a & = & \ & \ & 33\\
b & = & \ & \ & 44\\
c & = &73-25 & = & 48
\end{matrix}
Verificação: $\displaystyle p_{15} = \sqrt{44^2 + 33^2 + 48^2}=73$
Desprezando-se a condição de a diagonal $MN$ do tijolo ser um número inteiro, não é difícil, e sim trabalhoso, encontrar as dimensões e as diagonais do tijolo determinadas pelo matemático Halcke.
Como a menor dimensão do tijolo é $44$, basta achar os divisores pares de $44^2$menores que $44$.
Foi visto, anteriormente, que com os divisores $2$, $4$ e $8$, foram encontradas as seguintes diagonais: $d_1=485$, $d_2=244$ e $d_3=125$.
Subtraindo de $485$, $244$ e $125$, respectivamente, os divisores $2$, $4$ e $8$, obtém-se as seguintes dimensões: $485-2=483$, $244-4=240$ e $125-8=117$.
As dimensões do tijolo com as diagonais com números inteiros são uma das três:
\begin{matrix}
\color{blue}{a} & \ & \color{green}{b} &\ & \color{red}{c}\\
44 &\ & 240 &\ & 483\\
44 &\ & 117 &\ & 483\\
44 &\ & 117 &\ &240
\end{matrix}
Como para cada diagonal da base do tijolo há duas dimensõess, basta que combinemos três dimensões duas a duas e, em seguida, determinar a diagonal.
\begin{equation*}
\left\{
\begin{matrix}
44 & \text{e} & 240 & : & d_1 & = & \sqrt{44^2+240^2} & = & 244\\
44 & \text{e} & 483 & : & d_2 & = & \sqrt{44^2+483^2} & = & 485\\
240 & \text{e} & 483 & : & d_3 & = & \sqrt{240^2+483^2} & = & 539,34
\end{matrix}
\right.
\end{equation*}
\begin{equation*}
\left\{
\begin{matrix}
44 & \text{e} & 117 & : & d_1 & = & \sqrt{44^2+117^2} & = & 125\\
44 & \text{e} & 483 & : & d_2 & = & \sqrt{44^2+483^2} & = & 485\\
117 & \text{e} & 483 & : & d_3 & = & \sqrt{117^2+483^2} & = & 486,97
\end{matrix}
\right.
\end{equation*}
\begin{equation*}
\left\{
\begin{matrix}
44 & \text{e} & 117 & : & d_1 & = & \sqrt{44^2+117^2} & = & 125\\
44 & \text{e} & 240 & : & d_2 & = & \sqrt{44^2+240^2} & = & 244\\
117 & \text{e} & 240 & : & d_3 & = & \sqrt{117^2+240^2} & = & 267
\end{matrix}
\right.
\end{equation*}
As mesmas dimensões $(44,117,240)$ e as mesmas diagonais $(125,244,267)$ encontradas por Halcke.
$1)$ Com a condição de a diagonal $MN$ do tijolo de Euler ser um inteiro, apenas a diagonal da base é um número inteiro;
$2)$ Não existe tijolo de Euler perfeito;
$3)$ Exestem tijolos de Euler quase-perfeitos.
A conjectura de Beal - Casos particulares
O problema da arrumação das bolas em forma de quadrado

- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a}\ Dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a}\ dx = \frac{\displaystyle \text{arctg}\left( \frac{x}{\sqrt{a}}\right)}{\sqrt{a}}+C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2+a \neq...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Integral De $\displaystyle \frac{\sqrt{16-x^2}}{4x^2}dx$
Às vezes surgem dúvidas de leitores que valem um post. A resolução desta integral é interessante e usa o método de substituição trigonométrica. Seja a integral: \begin{equation*} \int \frac{\sqrt{16-x^2}}{4x^2}dx = I \end{equation*} Vejam o artigo...
- Método De Integração Por Partes
O método de integração por partes se aplica particularmente bem aos produtos de diferentes tipos de funções, tais como $x\cos(x)$, que é um produto entre um polinômio por uma função trigonométrica. Ao utilizar este método, a diferencial dada...
Matemática
O Tijolo de Euler
Por: Sebastião Vieira do Nascimento (Sebá)
Este artigo é sobre aplicação de ternos pitagóricos em um dos problemas insolúveis da Matemática.
O tijolo de Euler é um paralelepípedo regular de lados que são números inteiros $A$, $B$ e $C$, sendo $A > B > C$, cujas diagonais da face $D_{AB}$, $D_{AC}$ e $D_{BC}$ também são números inteiros. Se a diagonal principal é aquela que liga os pontos $M$ e $N$ do paralelepípedo, também for um número inteiro, o tijolo é dito perfeito. No entanto, não se conhece nenhum exemplo de um tijolo perfeito de Euler.

O tijolo simples de Euler imperfeito, com os menores valores para $A$, $B$ e $C$ que se conhece, tem as medidas: $A=240$, $B=117$ e $C=44$. As diagonais são :$D_{AB}=267$, $D_{AC}=244$ e $D_{BC}=125$. Foi descoberto em $1719$ pelo matemático Halcke.
Com o advento dos computadores, ficou muito mais fácil encontrar tijolos de Euler. Ao que parece, já são conhecido os $5.000$ menores tijolos de Euler, medidos pelo maior lado. Os $5$ primeiros são: $(240,117,44)$, $(275, 252,240)$, $(693,480,140)$, $(720,132,85)$ e $(792, 231, 160)$.
O problema matemático relacionado é encontrar uma ou mais fórmulas que produzam todos os tijolos de Euler perfeitos, casos existam. Até hoje, ninguém conseguiu isso.
Dedução das fórmulas que produzem todos os tijolos de Euler
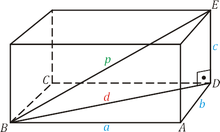
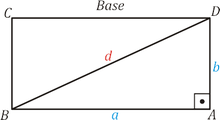
A figura abaixo é um paralelepípedo retângulo, onde são mostradas as diagonais da base e do paralelepípedo, respectivamente.


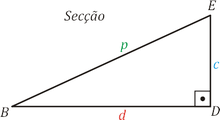
Como os triângulos $ABD$ e $DBE$ são retângulos e além disso, fazendo coincidir a diagonal da base com um dos catetos da diagonal do paralelepípedo, obtém-se:

A diagonal $d$ da base é tal que: $d^2 = a^2 + b^2$. Para a diagonal $p$ do paralelepípedo, temos que: $p^2 = c^2 + d^2$. Portanto, a fim de que os lados, a altura e a diagonal da base do paralelepípedo sejam números inteiros, basta que os dois ternos $(b, a, d)$ e $(d,c, p)$ sejam pitagóricos.
Já que a diagonal da base é um dos catetos do triângulo retângulo que forma a diagonal do paralelepípedo, logo as dimensões de cada tijolo e sua diagonal, em números inteiros, são dadas pela quadra $(b,a,c,p)$.
Seja $b$ o lado menor do tijolo. Como o triângulo $ABD$ tem que ser pitagórico, logo $d^2=a^2+b^2$ ou:
\begin{equation}
(d+a) = \frac{b^2}{d-a}
\end{equation}
Uma vez que $a$ e $d$ são inteiros, logo $(d-a)$ tem que dividir $b^2$ sem deixar resto. Logo, $(d-a)$ são os divisores positivos de $b^2$. Seja $b$ um primo ímpar. Os divisores de $b^2$ são: $b^2$ e $1$. Substituindo $b^2$, $b$
e $1$ em $(1)$, obtém-se os seguintes sistemas de equações:
\begin{equation*}
S_1=\left\{\begin{matrix}
d & - & a & = & b^2\\
d & + & a & = & 1
\end{matrix}\right.\\
\ \\
S_2=\left\{\begin{matrix}
d & - & a & = & b\\
d & + & a & = & b
\end{matrix}\right.\\
\ \\
S_3 = \left\{\begin{matrix}
d & - & a & = & 1\\
d & + & a & = & b^2
\end{matrix}\right.
\end{equation*}
Dos três sistemas de equações acima, somente o $S_3$ é compatível. Resolvendo o sistema $S_3$, obtém-se:
\begin{equation}
d=\frac{b^2+1}{2} \quad \text{e} \quad a=d-1
\end{equation}
Já que $p^2 = c^2 + d^2$, então:
\begin{equation}
p+c = \frac{d^2}{p-c}
\end{equation}
Como $b$ é um primo ímpar, logo $d$ pode ser uma primo ímpar ou um número composto ímpar.
Se $d$ for um primo ímpar, então chega-se aos mesmos resultados que se chegou para $b$, ou seja, três sistemas de equações $S_1$, $S_2$ e $S_3$, dos quais somente $S_3$ é compatível. E obtém-se para $p$ e $c$ as seguintes fórmulas:
\begin{equation}
p=\frac{d^2+1}{2} \quad \text{e} \quad c=p-1
\end{equation}
Resposta: Se $b$ e $d$ forem dois primos ímpares, então só existe um tijolo de Euler.
As medidas das diagonais do tijolo de Euler são dadas por:
\begin{equation*}
d=\frac{b^2+1}{2} \quad \text{diagonal da base do tijolo de Euler}\\
\ \\
p = \frac{d^2+1}{2} \quad \text{diagonal }MN\text{ do tijolo de Euler}
\end{equation*}
As dimensões do tijolo de Euler são dadas por:
$\quad a = d-1$ (lado maior)
$\quad b$ = (lado menor)
$\quad c=p-1$ (altura)
Como $d^2 = a^2+b^2$, então:
\begin{equation}
d+a = \frac{b^2}{d-a}
\end{equation}
Se $d-a=m$, então:
\begin{equation}
d+a=\frac{b^2}{m}
\end{equation}
Somando as equações membro a membro, obtém-se:
\begin{equation}
2d = \frac{b^2}{m}+m \quad \text{ou} \quad d=\frac{b^2+m^2}{2m} \quad \text{e} \quad a=d-m
\end{equation}
Suponha que $b$ seja par. Como $2d$ é sempre par, logo, a fim de que a soma $\displaystyle \frac{b^2}{m}+m$ seja par, $\displaystyle \frac{b^2}{m}$ e $m$ têm que ser ambos pares. Então, se $b$ for par, o número de soluções é igual ao número de divisores pares de $b^2$, menores que $b$, ou seja, $m < b$. Portanto, o número de triângulos pitagóricos é igual ao número de vezes em que $m$ (par) $<b$, dividir $b^2$ sem deixar resto.
Se $b$ for um número ímpar composto, então, como $2d$ é sempre par, logo, a fim de que a soma $\displaystyle \frac{b^2}{m}+m$ seja par, $m$ tem que ser ímpar. Então, o número de soluções é igual ao número de divisores de $b^2$ menores que $b^2$, ou seja, $m<b$. Portanto, o número de triângulos pitagóricos é igual ao número de vezes em que $m<b$ dividir $b^2$ sem deixar resto.
Já que $p^2=c^2+d^2$, então:
\begin{equation}
p+c = \frac{d^2}{p-c}
\end{equation}
Se $p-c=k$, então:
\begin{equation}
p+c = \frac{d^2}{k}
\end{equation}
Somando as duas equações membro a membro, obtém-se:
\begin{equation*}
2p = \frac{d^2}{k}+k \quad \text{ou} \quad p=\frac{d^2+k^2}{2k} \quad \text{e}\quad c=p-k
\end{equation*}
Se $d$ for um número par ou um ímpar não-primo, chega-se às mesmas conclusões que se chegou para $b$ par ou ímpar, ou seja, se $d$ for par, o número de triângulos pitagóricos é igual ao número de vezes em que $k$ (par) $< d$, dividir $d^2$ sem deixar resto. Se $d$ for ímpar composto, o número de triângulos pitagóricos é igual ao número de vezes em que $k < d$ dividir $d^2$ sem deixar resto.
As medidas das diagonais do tijolo de Euler são dadas por:
\begin{equation*}
d = \frac{b^2+m}{2} \quad \text{diagonal da base do tijolo de Euler}\\
\ \\
p=\frac{d^2 + k^2}{2k} \quad \text{diagonal }MN \text{ do tijolo de Euler}
\end{equation*}
As medidas das dimensões do tijolo de Euler são dadas por:
$\quad a=d-m$ (lado maior)
$\quad b=$ (lado menor)
$\quad c=p-k$ (altura)
Exemplo $1$:
Se o lado menor de um tijolo for $5cm$, quantos tijolos de Euler existem?Resolução:
Cálculo da diagonal da base do tijolo de Euler
\begin{equation*}d=\frac{5^2+1}{2}=13
\end{equation*}
Resposta: como $b=5$ e $d=13$ são ambos primos, logo, só existe um tijolo de Euler com o lado menor ou igual a $5cm$.
Cálculo da diagonal $MN$ do tijolo de Euler
\begin{equation*}p=\frac{13^2 + 1}{2}=85
\end{equation*}
Cálculo das dimensões do tijolo de Euler
\begin{matrix}a & = & 13-1 & = &12 \ cm\\
b & = & \ & \ & 5\ cm\\
c& = & 85-1& = &84 \ cm
\end{matrix}
Verificação
\begin{equation*}p=\sqrt{12^2 + 5^2 + 84^2} = \sqrt{144 + 25 + 7056} = 85
\end{equation*}
Sejam $D_{AB}$, $D_{AC}$ e $D_{BC}$, respectivamente, as diagonais do tijolo de Euler:
\begin{equation*}
D_{AB}=\sqrt{12^2+5^2}=13, \quad D_{AC}=\sqrt{12^2+84^2}=84,85 \quad \text{e} \quad D_{BC}=\sqrt{5^2+84^2}=84,15
\end{equation*}
Portanto, se a $D_{MN}$ for inteira, somente a $D_{AB}$ é inteira, ou seja, somente a diagonal da base do tijolo de Euler é inteira.
Exemplo $2$:
Se o lado menor de um tijolo for $7cm$, quantos tijolos de Euler existem?Resolução:
Cálculo da diagonal da base do tijolo de Euler
\begin{equation*}d = \frac{7^2+1}{2}=25\ cm
\end{equation*}
Como a diagonal da base do tijolo de Euler é um número composto ímpar, logo, o número de tijolos será igual ao número de vezes em que $m<25$ dividir $25^2$ sem deixar resto. Os divisores de $25^2$ menores que $25$ são: $1$ e $25$. Portanto, existem dois tijolos de Euler com o lado menor igual a $7$.
Cálculo da diagonal $MN$ do tijolo de Euler
\begin{equation*}1^o\text{ tijolo:}\ p_1=\frac{25^2+1}{2\cdot 1}=313\ cm\\
\ \\
2^o \text{tijolo:}\ p_2=\frac{25^2 + 5^2}{2\cdot 5}=65\ cm
\end{equation*}
Cálculo das dimensões de cada tijolo de Euler
$1^o$ tijolo:\begin{matrix}
a & = & d-1 & 25-1 & = & 24 \ cm\\
b & = & \ & \ & \ & 7\ cm\\
c & = & p-k & 313-1& = & 312 \ cm
\end{matrix}Verificação:
\begin{equation*}
p = \sqrt{24^2 + 7^2 + 312^2} = 313 \ cm
\end{equation*}
$2^o$ tijolo:
\begin{matrix}
a & = & d-1 & 25-1 & = & 24 \ cm\\
b & = & \ & \ & \ & 7\ cm\\
c & = & p-k & 65-5& = &60 \ cm
\end{matrix}
Verificação:
\begin{equation*}
p = \sqrt{24^2 + 7^2 + 60^2} = 65\ cm
\end{equation*}
Exemplo $3$:
O matemático Halcke encontrou apenas um tijolo de Euler com o menor lado igual a $44$. Quantos tijolos de Euler existem com o menor lado igual a $44$?Resolução
Os divisores de $44^2$, menores que $44$ são: $2$, $4$, $8$ e $16$. Portanto, tem-se que $m=2,4,8,16$.Cálculo das diagonais da base, principal e das dimensões do tijolo de Euler
Para: $\displaystyle d_1=\frac{44^2+2^2}{2 \times 2} = 485$, temos que os divisores de $485^2$, menores que $485$ são: $1,5,25$ e $97$.Para o divisor $1$:
\begin{equation*}
p_1=\frac{485^2 + 1}{2} = 117613
\end{equation*}
\begin{matrix}
a & = & d_1 - m & 485-2 & = & 483\\
b & = & \ & \ & \ & 44\\
c & = & p_1 - k & 117613-1& = & 117612
\end{matrix}
Verificação: $\displaystyle p_1 = \sqrt{44^2 + 483^2 + 117612^2}=117612$
Para o divisor $5$:
\begin{equation*}
p_2=\frac{485^2 + 5^2}{2 \times 5} = 23525
\end{equation*}
\begin{matrix}
a & = & \ & \ & 483\\
b & = & \ & \ &44\\
c & = & 23525-5 & = & 23520
\end{matrix}
Verificação: $\displaystyle p_2 = \sqrt{483^2 + 44^2 + 23520^2}=23525$
Para o divisor $25$:
\begin{equation*}
p_3=\frac{485^2 + 25^2}{2 \times 25} =4717
\end{equation*}
\begin{matrix}
a & = & \ & \ & 483\\
b & = & \ & \ &44\\
c & = & 4717-25 & = & 4692
\end{matrix}
Verificação: $\displaystyle p_3 = \sqrt{483^2 + 44^2 + 4692^2}=4717$
Para o divisor $97$:
\begin{equation*}
p_4=\frac{485^2 + 97^2}{2 \times 97} =1261
\end{equation*}
\begin{matrix}
a & = & \ & \ & 483\\
b & = & \ & \ &44\\
c & = & 1261-97 & = & 1164
\end{matrix}
Verificação: $\displaystyle p_4 = \sqrt{483^2 + 44^2 + 1164^2}=1261$
Para: $\displaystyle d_2=\frac{44^2+4^2}{2 \times 4} = 244$, temos que os divisores pares de $244^2$, menores que $\displaystyle \frac{244}{2}$ são: $2,4,8$ e $16$.
Para o divisor $2$:
\begin{equation*}
p_5=\frac{244^2 + 2^2}{2 \times 2} =14885
\end{equation*}
\begin{matrix}
a & = & 244-4 & = & 240\\
b & = & \ & \ &44\\
c & = & 14885-2 & = & 14883
\end{matrix}
Verificação: $\displaystyle p_5 = \sqrt{240^2 + 44^2 + 14883^2}=14885$
Para o divisor $4$:
\begin{equation*}
p_6=\frac{244^2 + 4^2}{2 \times 4} =7444
\end{equation*}
\begin{matrix}
a & = & \ & \ & 240\\
b & = & \ & \ &44\\
c & = & 7444-4 & = & 7440
\end{matrix}
Verificação: $\displaystyle p_6 = \sqrt{240^2 + 44^2 + 7440^2}=7444$
Para o divisor $8$:
\begin{equation*}
p_7=\frac{244^2 + 8^2}{2 \times 8} =3725
\end{equation*}
\begin{matrix}
a & = & \ & \ & 240\\
b & = & \ & \ &44\\
c & = & 3725-8 & = & 3717
\end{matrix}
Verificação: $\displaystyle p_7 = \sqrt{240^2 + 44^2 + 3717^2}=3725$
Para o divisor $16$:
\begin{equation*}
p_8=\frac{244^2 + 16^2}{2 \times 16} =1865,5\\
\end{equation*}
$p_8$ não é inteiro, porque $\displaystyle \frac{d^2}{k}=\frac{244^2}{16}$ é ímpar.
Para: $\displaystyle d_3=\frac{44^2+8^2}{2 \times 8} =125$, temos que os divisores pares de $125^2$, menores que $125$ são: $1,5$ e $25$.
Para o divisor $1$:
\begin{equation*}
p_9=\frac{125^2 +1}{2} =7813
\end{equation*}
\begin{matrix}
a & = & 125-8 & = & 117\\
b & = & \ & \ &44\\
c & = & 7813-1 & = & 7812
\end{matrix}
Verificação: $\displaystyle p_9 = \sqrt{117^2 + 44^2 + 7812^2}=7813$
Para o divisor $5$:
\begin{equation*}
p_{10}=\frac{125^2 +5^2}{2 \times 5} =1565
\end{equation*}
\begin{matrix}
a & = & \ & \ & 117\\
b & = & \ & \ &44\\
c & = & 1565-5 & = & 1560
\end{matrix}
Verificação: $\displaystyle p_{10} = \sqrt{117^2 + 44^2 + 1560^2}=1565$
Para o divisor $25$:
\begin{equation*}
p_{11}=\frac{125^2 +25^2}{2 \times 25} =325
\end{equation*}
\begin{matrix}
a & = & \ & \ & 117\\
b & = & \ & \ &44\\
c & = & 325-25 & = & 300
\end{matrix}
Verificação: $\displaystyle p_{11} = \sqrt{117^2 + 44^2 + 300^2}=325$
Para: $\displaystyle d_4=\frac{44^2+16^2}{2 \times 16} = 68,$
$d_4$ não é inteiro porque $\displaystyle \frac{b^2}{m}=\frac{44^2}{16}$ é ímpar.
Para: $\displaystyle d_5=\frac{44^2+22^2}{2 \times 22} = 55$, temos que os divisores de $55^2$, menores que $55$ são: $1,5,11$ e $25$.
Para o divisor $1$:
\begin{equation*}
p_{12}=\frac{55^2 +1}{2} =1513
\end{equation*}
\begin{matrix}
a & = & 55-22 & = & 33\\
b & = & \ & \ &44\\
c & = & 1513-1 & = & 1512
\end{matrix}
Verificação: $\displaystyle p_{12} = \sqrt{44^2 + 33^2 + 1512^2}=1513$
Para o divisor $5$:
\begin{equation*}
p_{13}=\frac{55^2 +5^2}{2 \times 5} =305
\end{equation*}
\begin{matrix}
a & = & \ & \ & 33\\
b & = & \ & \ &44\\
c & = & 305-5 & = & 300
\end{matrix}
Verificação: $\displaystyle p_{13} = \sqrt{44^2 + 33^2 + 300^2}=305$
Para o divisor $11$:
\begin{equation*}
p_{14}=\frac{55^2 +11^2}{2 \times 11} =143
\end{equation*}
\begin{matrix}
a & = & \ & \ & 33\\
b & = & \ & \ & 44\\
c & = & 143-11 & = & 132
\end{matrix}
Verificação: $\displaystyle p_{14} = \sqrt{44^2 + 33^2 + 132^2}=143$
Para o divisor $25$:
\begin{equation*}
p_{15}=\frac{55^2 +25^2}{2 \times 25} =73
\end{equation*}
\begin{matrix}
a & = & \ & \ & 33\\
b & = & \ & \ & 44\\
c & = &73-25 & = & 48
\end{matrix}
Verificação: $\displaystyle p_{15} = \sqrt{44^2 + 33^2 + 48^2}=73$
Resposta:
Existem $15$ tijolos de Euler com o menor lado igual a $44$.Desprezando-se a condição de a diagonal $MN$ do tijolo ser um número inteiro, não é difícil, e sim trabalhoso, encontrar as dimensões e as diagonais do tijolo determinadas pelo matemático Halcke.
Como a menor dimensão do tijolo é $44$, basta achar os divisores pares de $44^2$menores que $44$.
Foi visto, anteriormente, que com os divisores $2$, $4$ e $8$, foram encontradas as seguintes diagonais: $d_1=485$, $d_2=244$ e $d_3=125$.
Subtraindo de $485$, $244$ e $125$, respectivamente, os divisores $2$, $4$ e $8$, obtém-se as seguintes dimensões: $485-2=483$, $244-4=240$ e $125-8=117$.
As dimensões do tijolo com as diagonais com números inteiros são uma das três:
\begin{matrix}
\color{blue}{a} & \ & \color{green}{b} &\ & \color{red}{c}\\
44 &\ & 240 &\ & 483\\
44 &\ & 117 &\ & 483\\
44 &\ & 117 &\ &240
\end{matrix}
Como para cada diagonal da base do tijolo há duas dimensõess, basta que combinemos três dimensões duas a duas e, em seguida, determinar a diagonal.
\begin{equation*}
\left\{
\begin{matrix}
44 & \text{e} & 240 & : & d_1 & = & \sqrt{44^2+240^2} & = & 244\\
44 & \text{e} & 483 & : & d_2 & = & \sqrt{44^2+483^2} & = & 485\\
240 & \text{e} & 483 & : & d_3 & = & \sqrt{240^2+483^2} & = & 539,34
\end{matrix}
\right.
\end{equation*}
\begin{equation*}
\left\{
\begin{matrix}
44 & \text{e} & 117 & : & d_1 & = & \sqrt{44^2+117^2} & = & 125\\
44 & \text{e} & 483 & : & d_2 & = & \sqrt{44^2+483^2} & = & 485\\
117 & \text{e} & 483 & : & d_3 & = & \sqrt{117^2+483^2} & = & 486,97
\end{matrix}
\right.
\end{equation*}
\begin{equation*}
\left\{
\begin{matrix}
44 & \text{e} & 117 & : & d_1 & = & \sqrt{44^2+117^2} & = & 125\\
44 & \text{e} & 240 & : & d_2 & = & \sqrt{44^2+240^2} & = & 244\\
117 & \text{e} & 240 & : & d_3 & = & \sqrt{117^2+240^2} & = & 267
\end{matrix}
\right.
\end{equation*}
As mesmas dimensões $(44,117,240)$ e as mesmas diagonais $(125,244,267)$ encontradas por Halcke.
Conclusão
Baseando-se nos resultados obtidos, pode-se elaborar as três seguintes conjecturas:$1)$ Com a condição de a diagonal $MN$ do tijolo de Euler ser um inteiro, apenas a diagonal da base é um número inteiro;
$2)$ Não existe tijolo de Euler perfeito;
$3)$ Exestem tijolos de Euler quase-perfeitos.
Autor
Este artigo foi cedido gentilmente por Sebastião Vieira do Nascimento (Sebá). Professor Titular (por concurso) aposentado da UFCG – PB, além de colaborador deste blog.Veja mais:
Sobre os primos gêmeosA conjectura de Beal - Casos particulares
O problema da arrumação das bolas em forma de quadrado

- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a}\ Dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a}\ dx = \frac{\displaystyle \text{arctg}\left( \frac{x}{\sqrt{a}}\right)}{\sqrt{a}}+C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2+a \neq...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Integral De $\displaystyle \frac{\sqrt{16-x^2}}{4x^2}dx$
Às vezes surgem dúvidas de leitores que valem um post. A resolução desta integral é interessante e usa o método de substituição trigonométrica. Seja a integral: \begin{equation*} \int \frac{\sqrt{16-x^2}}{4x^2}dx = I \end{equation*} Vejam o artigo...
- Método De Integração Por Partes
O método de integração por partes se aplica particularmente bem aos produtos de diferentes tipos de funções, tais como $x\cos(x)$, que é um produto entre um polinômio por uma função trigonométrica. Ao utilizar este método, a diferencial dada...
