Matemática

Solucionando o Problema do Aniversário

Em postagem anterior, foi proposto um problema que pode ser enunciado do seguinte modo:

Qual é a probabilidade de que, em um grupo de $$49$$ pessoas, existam pelo menos duas que façam aniversário no mesmo dia?

Supomos, inevitavelmente, que o leitor já tenha estudado algo sobre probabilidades e começamos lembrando que a probabilidade $$P(X)$$ de ocorrência de um evento $$X$$ pode ser dada pela expressão

$$P(X)=\frac{n}{m}$$

onde $$n$$ representa o número de resultados favoráveis ao evento $$X$$ e $$m$$ representa o número de resultados possíveis. Lembremos também que a probabilidade $$P(X')$$ do evento $$X$$ não ocorrer é dada por

$$P(X')=1-P(X)$$

Com estes fatos em mente, vamos convencionar que ocorrer o evento $$A$$ significa "existir no mínimo duas pessoa que aniversariam no mesmo dia". Portanto é $$P(A)$$ que devemos achar para responder a pergunta em negrito acima.

Entretanto, num primeiro momento, em vez de calcularmos diretamente a probabilidade de ocorrência do evento $$A$$ vamos calcular a probabilidade do evento $$A$$ não ocorrer, (em outros termos: vamos calcular a probabilidade de que todas as $$49$$ pessoas aniversariem em dias diferentes, evento este que chamaremos de $$A'$$) e em seguida faremos uso da fórmula

$$P(A')=1-P(A) \Leftrightarrow P(A)=1-P(A')$$

Comecemos, então, calculando "o número de resultados possíveis". Observe que fazer este cálculo é o mesmo que responder a seguinte questão: de quantas maneiras diferentes $$49$$ pessoas podem fazer aniversário em um ano de $$365$$ dias?

Ora, para a primeira pessoa há $$365$$ possibilidades (afinal ela pode ter nascido em qualquer dia do ano);
De igual modo, para a segunda pessoa há $$365$$ possibilidades;
Semelhantemente, para a terceira pessoa há $$365$$ possibilidades;
Para a quarta pessoa há $$365$$ possibilidades;

$$\vdots$$

Para a quadragésima oitava pessoa há $$365$$ possibilidades;
E por fim, para quadragésima nona pessoa também há $$365$$ possibilidades.

Concluímos assim (em virtude do princípio fundamental da contagem) que existem $$365\times365\times\cdots\times365=365^{49}$$ modos diferentes deste grupo de $$49$$ pessoas aniversariarem.

Calculemos, agora, o número de resultados favoráveis ao evento $$A'$$ (ou seja, favoráveis ao evento "todas aniversariarem em dias diferentes"). Observe que fazer este cálculo é o mesmo que responder a seguinte questão: em um ano de $$365$$ dias, quantos modos existem de todas as $$49$$ pessoas fazerem aniversário em dias distintos?

Ora, para a primeira pessoa há $$365$$ possibilidades (afinal ela pode ter nascido em qualquer dia do ano);
Já para a segunda pessoa há $$364$$ possibilidades (pois ela não pode ter nascido no mesmo dia em que a primeira pessoa);
Para a terceira pessoa, há $$363$$ possibilidades (pois a data de seu nascimento não pode coincidir com a data do nascimento das duas pessoas anteriores);
Para a quarta pessoa, há $$362$$ possibilidades;

$$\vdots$$

Para a quadragésima oitava pessoa há $$365-47=318$$ possibilidades;
E por fim, para quadragésima nona pessoa há $$365-48=317$$ possibilidades (pois seu aniversário não pode coincidir com o aniversário de alguma das outras quarenta e oito pessoas).

Portanto (novamente em virtude do princípio fundamental da contagem) concluímos que o número de modos de, num grupo de $$49$$ pessoas, todas aniversariarem em dias diferentes é $$365\times364\times\cdots\times318\times317$$.

Conclusões:

A probabilidade de todas as $$49$$ pessoas aniversariarem em dias diferentes é

$$P(A')=\frac{365\times364\cdots\times317}{365^{49}}\cong0,034$$

A probabilidade de que dentre as $$49$$ pessoas existam pelo menos duas que façam aniversário no mesmo dia será, portanto,

$$P(A)=1-P(A')\cong1-0,034\cong0,96=96\%$$

Assim o problema fica resolvido sendo que, naquela data, as chances do BLOG MANTHANO possuir pelo menos dois seguidores nascidos no mesmo dia era de quase $$100\%$$. Surpreendente, não?

Observações:

1) Vale ressaltar que no cálculo apresentado "desprezamos variações na distribuição, tais como anos bissextos, gêmeos, variações sazonais ou semanais, e assumimos que $$365$$ possíveis aniversários são todos igualmente prováveis" [fragmento entre aspas extraído da wikipédia].

2) Note que o número de resultados favoráveis ao evento $$A'$$ pode ser escrito de uma maneira mais compacta (que foi útil para calcular o valor de $$P(A')$$ através do site Wolfram Alpha):

$$365\times364\times\cdots\times318\times317=\frac{365!}{(365-49)!}=\frac{365!}{316!}$$

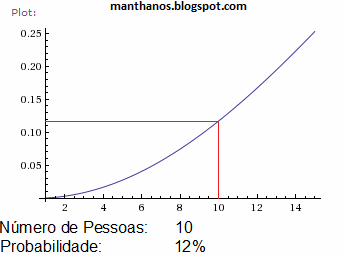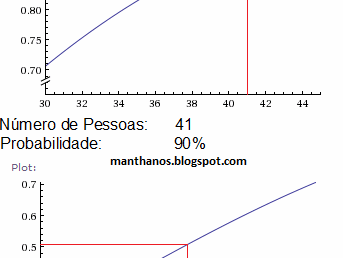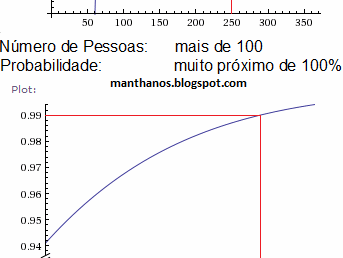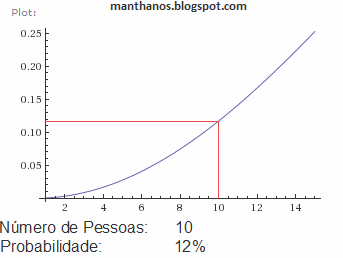
3) A animação abaixo mostra a "curva do aniversário" em seis níveis de zoom diferentes, fornecendo uma estimativa para a probabilidade de que haja pelo menos duas pessoas em cada grupo que façam aniversário no mesmo dia:

gráficos feitos no Wolfram Alpha

4) Escrevendo a probabilidade mencionada em função do número de pessoas do grupo obtemos uma função de variável discreta, logo seu gráfico não poderia apresentar traçado contínuo tal qual o da figura acima. Ressaltamos, porém, que para traçar os gráficos adotamos um modelo contínuo (que, para fins de cálculo, não apresenta nenhum inconveniente). Mais precisamente usamos a seguinte expressão:

$$f(x)=1-\frac{365!}{(365-x)!365^x}$$

5) Muito embora para grupos com cerca de $$200$$ ou $$300$$ pessoas a probabilidade (de haver pelos menos duas que nasceram no mesmo dia) ser gigantesca, a certeza absoluta só poderá ser alcançada em grupos com mais de $$365$$ pessoas.

Referências: a matemática do ensino médio, volume 2 (de Elon e outros); Wikipédia.

Erros podem ser relatados aqui.

- Questão 39 ? Docente ? Estatística ? If/mt ? 2.012
Cargo: Docente - EstatísticaAno: 2012Órgão: Instituto Federal ? Mato GrossoInstituição: UFMT Considere dois eventos A e B , mutuamente exclusivos, e suponha que a probabilidade do evento A é 0,3 ( P[A] = 0,3) e...

- Probabilidade
PROBABILIDADE A história da teoria das probabilidades, teve início com os jogos de cartas, dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo da probabilidade. A teoria da probabilidade permite que se calcule...

- Noções De Probabilidade
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...

- Probabilidade De Dois Eventos Sucessivos Ou Simultâneos
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com ...

- Probabilidade
PROBABILIDADE A história da teoria das probabilidades, teve início com os jogos de cartas, dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo da probabilidade. A teoria da probabilidade permite que se calcule...

Matemática