Matemática

Técnica de Multiplicação - Tabuada II - Tabuada Digital (conclusão)

O procedimento de realizar multiplicações por meio das mãos pode se estender para outras dezenas.

Cada dezena é dividida em duas partes: (i) com unidades 1, 2, 3, 4, e 5, que consideramos como Método I, que são os casos que ocorrem nas postagens Técnicade Multiplicação - Tabuada II - Tabuada Digital e Técnica de Multiplicação -Tabuada II - Tabuada Digital (cont.), e; (ii) com unidades 6, 7, 8, 9, e 0, que consideramos como Método II, que é os caso que ocorre na postagem Técnica deMultiplicação - Tabuada II - Tabuada Digital (cont.).

No Método I são utilizados os dedos que estão acima dos dedos que encostamos e no Método II desconsideramos estes dedos.

Em determinado momento do procedimento somamos aos dedos encostados a quantidade de dedos que se encontram abaixo deles. O total é multiplicado por um determinado valor sendo para o Método I é dado por {10 ? (d? 1)} e para o Método II é dado por {10 ? d}, onde d é o valor da dezena.

No final do processo se realiza a soma de determinado valor que para o Método I é dado por {100 ? (d ? 1)²} e para o Método II é dado por {100 ? d ? (d? 1)}, onde d é o valor da dezena.

Na tabela abaixo temos valores para algumas dezenas, para o leitor ter uma ideia do processo. Nesta tabela temos o valor da constante aditiva que são somados no ultimo passo para obter o produto final.

Dezena	Meia ? Dezena	Produto dos Dedos Somados	Constante Aditiva
1	1 ~ 5	0	0
1	6 ~10	10	0
2	11 ~ 15	10	100
2	16 ~ 20	20	200
3	21 ~ 25	20	400
3	26 ~ 30	30	600
4	31 ~ 35	30	900
4	36 ~ 40	40	1.200
5	41 ~ 45	40	1.600
5	46 ~ 50	50	2.000

Tabela 1: O Método I está em azul e o Método II em vermelho.

Exemplo (01): segundo a tabela produtos entre valores 41, 42, 43, 44 e 45, são do Método I, a soma dos dedos é multiplicada por 40 e temos que adicionar 1.600 no ultima passo para obter o resultado final.

Testando com o produto de 42x43:

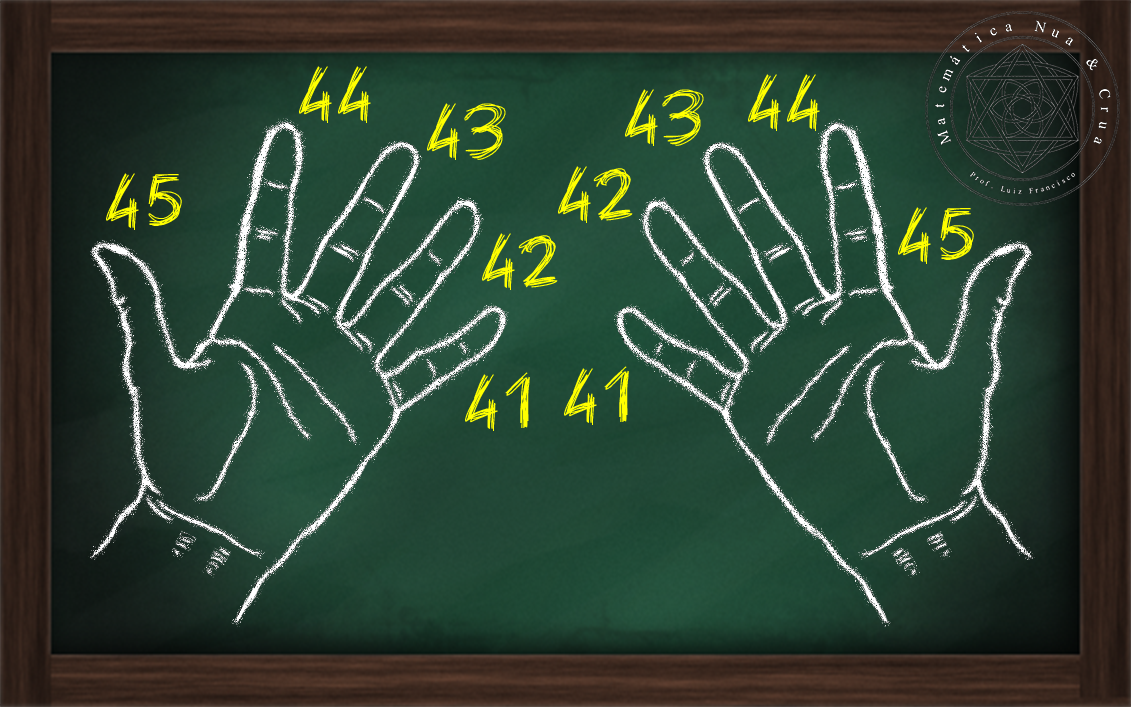Figura 1: Identificação de cada dedo de 41 à 45. Observe que você deve olhar para a palma das mãos. Cole um adesivo para poder praticar.

Figura 2: Encostando o dedo correspondente ao 42 de uma das mão no dedo correspondente ao 43 da outra mão.

(i) 3 x 2 = 6;

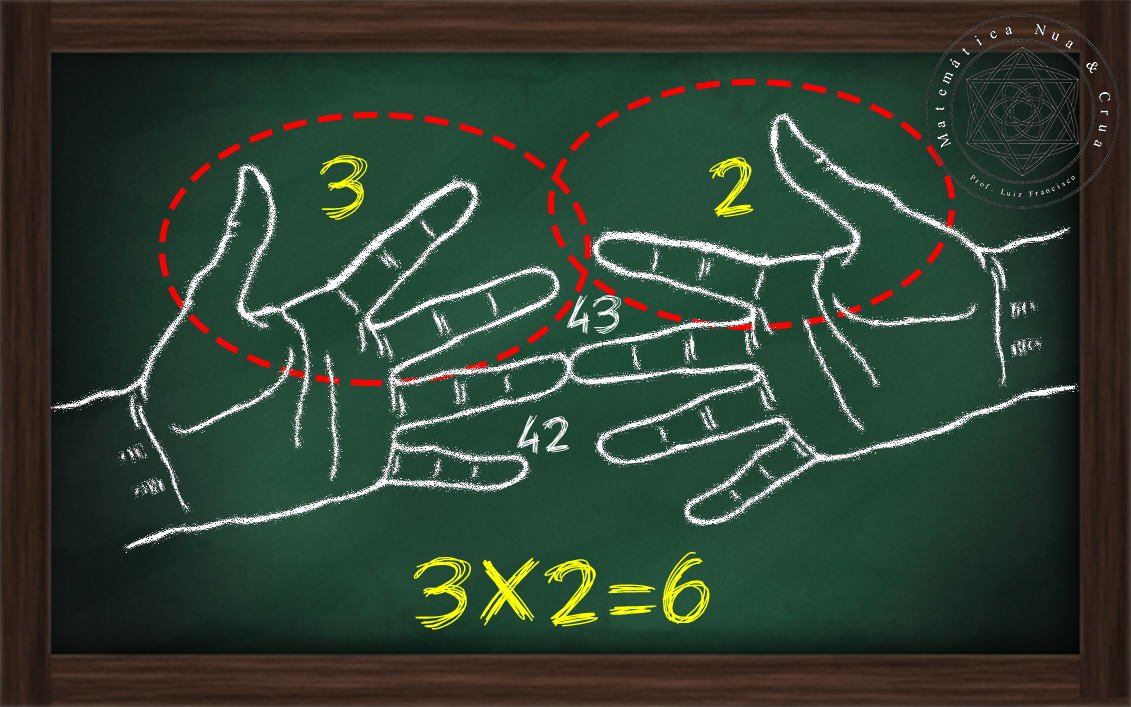Figura 3: Primeira etapa.

(ii) 2 + 3 = 5; 5 x 40 = 200

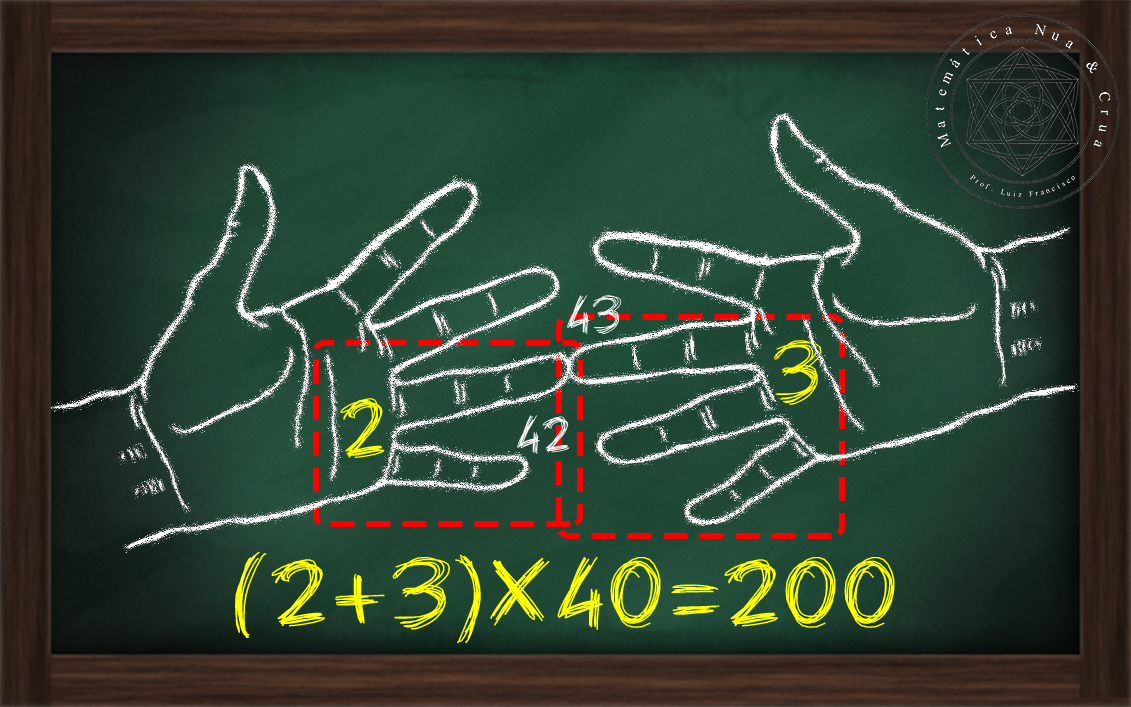Figura 4: Segunda etapa.

(iii) 42 x 43 = 6 + 200 + 1.600 = 1.806

Figura 5: Terceira etapa e Resultado final.

Exemplo (02): produtos entre valores 76, 77, 78, 79 e 80, são da 8º dezena e do Método II, a soma dos dedos é multiplicada por {10 ? 8} = 80 e temos que adicionar {100 ? 8 ? (8 ? 1)} = 5.600 no ultima passo para obter o resultado final.

Testando com o produto de 77x78:

Figura 6: Identificação de cada dedo de 76 à 80. Observe que você deve olhar para a palma das mãos. Cole um adesivo para poder praticar.

Figura 7: Encostando o dedo correspondente ao 77 de uma das mão no dedo correspondente ao 78 da outra mão.

(i) 3 x 2 = 6;

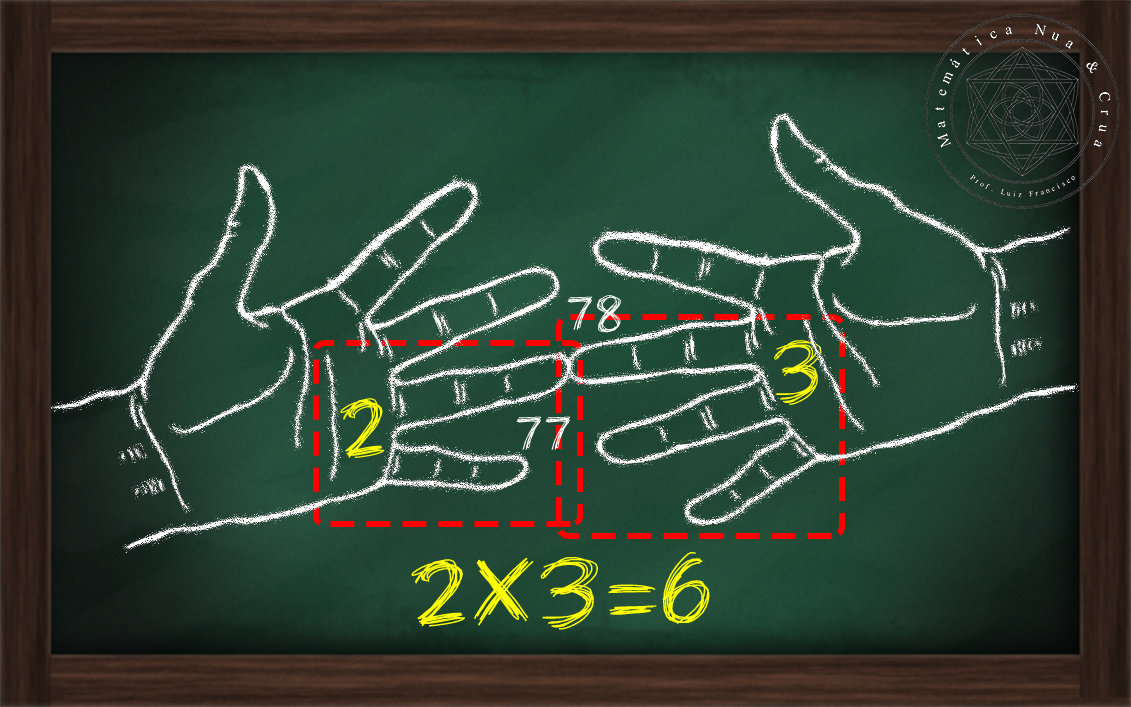Figura 8: Primeira etapa.

(ii) 2 + 3 = 5; 5 x 80 = 400

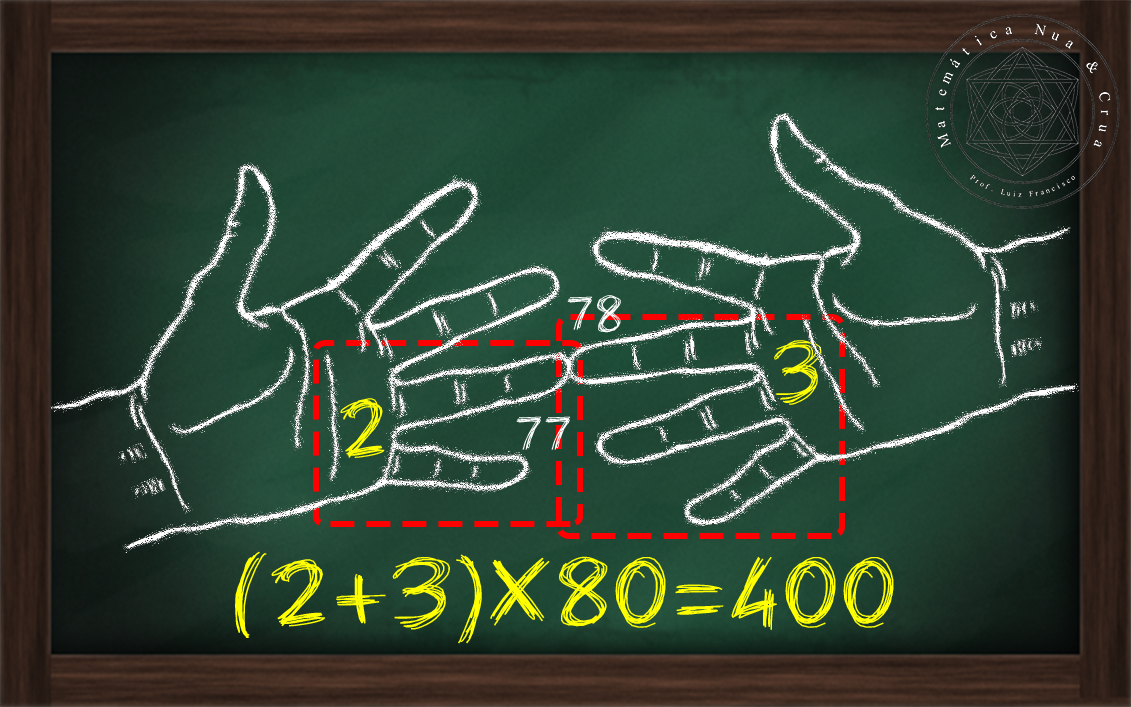Figura 9: Segunda etapa.

(iii) 77 x 78 = 6 + 400 + 5.600 = 6.006

Figura 10: Terceira etapa e Resultado final.

Recomendações para quem quer se aventura por estes cálculos digitais:

(i)treine bastante, uma dezena de cada vez;

(ii)tente compreender o processo e não apenas decorar;

(iii) Nathan Altshiller Court, em ?Mathematics in Fun and in Earnest? sugere a seguinte equação geral:

(a + x) · (a + y) = 2 · a · (x + y) + (a ? x) · (a ? y)

Que pode ser escrito na forma:

(a + x) · (a + y) = a · (x + y) + x · y + a²

Sendo xe yo digito das unidades dos números multiplicados e a o digito das dezenas mu1tiplicado por 10.

Exemplo: 67x68, temos x = 7, y = 8 e a = 60 (6 · 10).

a · (x + y) + x · y + a² ? 60 · (7 + 8) + 7 · 8 + 60² = 4.556

Fonte: GARDNER, Martin. Mathematical Magic Show. The Mathematical Association of America. Washington, D. C. 1.989.

- Lembrando Do Seno E Cosseno Dos Ângulos Notáveis
Para aqueles que apreciam formas diferentes para auxiliar os alunos a lembrarem de determinadas constantes matemáticas, apresento uma método para lembrar os valores dos senos e cossenos dos ângulos notáveis. Este método é uma alternativa para as...

- Técnica De Multiplicação - Tabuada Ii - Tabuada Digital (cont.)
Ante de continuar recomento que leia e pratique a forma de multiplicar apresentado na postagem anterior (Técnica de Multiplicação - Tabuada II - Tabuada Digital). Nesta postagem apresento uma forma semelhante onde utilizaremos os seus dedos para realizar...

- Técnica De Multiplicação - Tabuada Ii - Tabuada Digital
Em alguns lugares do mundo, camponeses ainda se utilizam dos seus dedos para realizar multiplicações envolvendo os números: 6, 7, 8, 9 e 10, ou seja, multiplicações como 6x7, 8x8, 10x6, etc. Para isso, são necessários: (i) conhecer as tábuas de...

- Jura? Tabuada Do 9
Oiii pessoal, Como prometido, hoje vamos aprender, com o uso dos dedos, a tabuada dos 9. A partir de agora, ninguém mais vai errar as multiplicações 9x7, 9x9... Vamos lá? Diferentemente do método de ontem, vamos assorciar os dedos de cada mão...

- Tabuada
Tabuada Muito interessante. Para visualizar a tabuada do 9 nos dedos, posicione as duas mãos conforme a figura: Dobramos o dedo que representa o fator diferente de nove, lendo como numeral os algarismos representados pelos dedos anteriores e posteriores...

Matemática