Matemática
Viggo Brun nasceu em $13$ de outubro de $1885$ em Lier, Noruega e morreu em $15$ de agosto de 1978 me Drobak.
Em $1923$ tornou-se professor no Instituto Norueguês de Tecnologia e em $1946$ tornou-se professor na Universidade de Oslo, onde aposentou-se em $1955$, aos $70$ anos de idade.
Em $1915$ introduziu um novo método, baseado na versão de Legendre do Crivo de Eratóstens, conhecido hoje como Crivo de Brun, que aborda problemas como a Conjectura de Goldbach e os Primos Gêmeos. Utilizou seu Crivo para provar que existem infinitos inteiros $n$, tal que $n$ e $n+2$ tem no máximo nove fatores primos ($9$-quasi-primos) e que todo inteiro par grande é a soma de dois números $9$-quasi-primos ($9$ ou menor).
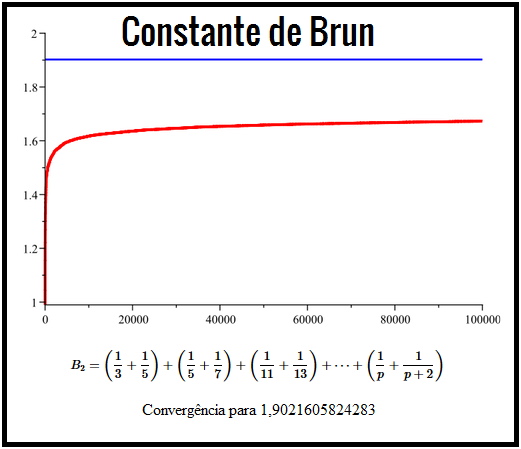
Sobre os Números Primos Gêmeos, Brun mostrou que a soma dos recíprocos dos pares Primos Gêmeos convergem para um valor finito, atualmente denominado por Constante de Brun.
A Constante de Brun vale hoje aproximadamente $1,9021605824283$ e é calculada através de uma série convergente, dada pela soma infinita:
\begin{equation*}
B_2 = \left(\frac{1}{3}+\frac{1}{5}\right)+\left(\frac{1}{5}+\frac{1}{7}\right)+\left(\frac{1}{11}+\frac{1}{13}\right)+\cdots+\left(\frac{1}{p}+\frac{1}{p+2}\right)
\end{equation*}
Abaixo segue uma lista dos $100$ primeiros números primos gêmeos:
Clique aqui para ver os $10.000$ primeiros números primos gêmeos.
Já para a soma dos inversos do números primos, temos uma série divergente, que foi demonstrada pelo gênio Euler no século $XVIII$:
\begin{equation*}
B_1=\sum_{i=1}^\infty \frac{1}{p_i}=\frac{1}{2}+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\frac{1}{11}+\frac{1}{13}+\frac{1}{17}+\frac{1}{19}+\cdots +\frac{1}{p}=\infty
\end{equation*}
Quantos números primos existem?
Construindo uma sequência de números não-primos

- Resolução Da Integral $\displaystyle \int \frac{x^2+1}{x^2-1}dx$
Nesta postagem, veremos que: \begin{equation*} \int \frac{x^2+1}{x^2-1}dx = x+ \ln|x-1|- \ln|x+1| + C \end{equation*} onde $x \in \mathbb{R}$, sendo $x \neq \pm 1$. Seja a integral: \begin{equation*} I = \int \frac{x^2+1}{x^2-1}dx \end{equation*} Decompomos...
- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a^2}dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a^2}\ dx = \frac{1}{a}\text{arctg}\left(\frac{x}{a}\right) + C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2 + a^2 \neq 0$. Seja a integral:...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Fórmula Da Soma Dos Termos De Uma P.g. Infinita
Vimos no post anterior sobre a demonstração da fórmula para a soma dos termos de uma P.G. finita: \begin{equation} S_n=\frac{a_1(q^n-1)}{q-1} \end{equation} Se tivermos uma $P.G.$ infinita na forma: \begin{equation} (a_1, a_2, a_3, \cdots ,a_n, \cdots...
Matemática
A Constante de Brun
Viggo Brun nasceu em $13$ de outubro de $1885$ em Lier, Noruega e morreu em $15$ de agosto de 1978 me Drobak.
Em $1923$ tornou-se professor no Instituto Norueguês de Tecnologia e em $1946$ tornou-se professor na Universidade de Oslo, onde aposentou-se em $1955$, aos $70$ anos de idade.
Em $1915$ introduziu um novo método, baseado na versão de Legendre do Crivo de Eratóstens, conhecido hoje como Crivo de Brun, que aborda problemas como a Conjectura de Goldbach e os Primos Gêmeos. Utilizou seu Crivo para provar que existem infinitos inteiros $n$, tal que $n$ e $n+2$ tem no máximo nove fatores primos ($9$-quasi-primos) e que todo inteiro par grande é a soma de dois números $9$-quasi-primos ($9$ ou menor).

Sobre os Números Primos Gêmeos, Brun mostrou que a soma dos recíprocos dos pares Primos Gêmeos convergem para um valor finito, atualmente denominado por Constante de Brun.
A Constante de Brun vale hoje aproximadamente $1,9021605824283$ e é calculada através de uma série convergente, dada pela soma infinita:
\begin{equation*}
B_2 = \left(\frac{1}{3}+\frac{1}{5}\right)+\left(\frac{1}{5}+\frac{1}{7}\right)+\left(\frac{1}{11}+\frac{1}{13}\right)+\cdots+\left(\frac{1}{p}+\frac{1}{p+2}\right)
\end{equation*}
Abaixo segue uma lista dos $100$ primeiros números primos gêmeos:
3, 5, 7, 11, , 13, 17, 19, 29, 31, 41, 43, 59, 61, 71, 73, 101, 103, 107, 109, 137, 139, 149, 151, 179, 181, 191, 193, 197, 199, 227, 229, 239, 241, 269, 271, 281, 283, 311, 313, 347, 349, 419, 421, 431, 433, 461, 463, 521, 523, 569, 571, 599, 601, 617, 619, 641, 643, 659, 661, 809, 811, 821, 823, 827, 829, 857, 859, 881, 883, 1019, 1021, 1031, 1033, 1049, 1051, 1061, 1063, 1091, 1093, 1151, 1153, 1229, 1231, 1277, 1279, 1289, 1291, 1301, 1303, 1319, 1321, 1427, 1429, 1451, 1453, 1481, 1483, 1487, 1489
Clique aqui para ver os $10.000$ primeiros números primos gêmeos.
Já para a soma dos inversos do números primos, temos uma série divergente, que foi demonstrada pelo gênio Euler no século $XVIII$:
\begin{equation*}
B_1=\sum_{i=1}^\infty \frac{1}{p_i}=\frac{1}{2}+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\frac{1}{11}+\frac{1}{13}+\frac{1}{17}+\frac{1}{19}+\cdots +\frac{1}{p}=\infty
\end{equation*}
Veja mais:
Sobre os primos gêmeosQuantos números primos existem?
Construindo uma sequência de números não-primos

- Resolução Da Integral $\displaystyle \int \frac{x^2+1}{x^2-1}dx$
Nesta postagem, veremos que: \begin{equation*} \int \frac{x^2+1}{x^2-1}dx = x+ \ln|x-1|- \ln|x+1| + C \end{equation*} onde $x \in \mathbb{R}$, sendo $x \neq \pm 1$. Seja a integral: \begin{equation*} I = \int \frac{x^2+1}{x^2-1}dx \end{equation*} Decompomos...
- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a^2}dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a^2}\ dx = \frac{1}{a}\text{arctg}\left(\frac{x}{a}\right) + C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2 + a^2 \neq 0$. Seja a integral:...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
- Fórmula Da Soma Dos Termos De Uma P.g. Infinita
Vimos no post anterior sobre a demonstração da fórmula para a soma dos termos de uma P.G. finita: \begin{equation} S_n=\frac{a_1(q^n-1)}{q-1} \end{equation} Se tivermos uma $P.G.$ infinita na forma: \begin{equation} (a_1, a_2, a_3, \cdots ,a_n, \cdots...
