Matemática
- Desafio - Física
Na figura, um bloco sobe um plano inclinado, com velocidade inicial $$V_0$$. Considere $$\mu$$ o coeficiente de atrito entre o bloco e a superfície. Indique sua velocidade ao passar pela posição inicial. A. $$V_0\sqrt{\frac{sen\theta - \mu cos\theta}{sen\theta...
- Tetravista De Z²
As três Tetravistas mostradas na exposição são uma tentativa para entender melhor gráficos de funções complexas. O gráfico duma função de variável complexa está no espaço complexo bidimensional, que pode ser identificado naturalmente com...
- Triângulo De Pascal
O Triângulo de Pascal é um triângulo numérico formado por Binômios de Newton (leia o post sobre binômio de Newton) $$\begin{pmatrix}n\\k\end{pmatrix}$$, onde $$n$$ representa o número da linha (posição vertical) e $$K$$ representa o número da...
- Projeção Ortogonal De Um Segmento De Reta Sobre Um Plano
$1)$ Projeção de um ponto Definição $1$: Chama-se projeção ortogonal de um ponto $P$ sobre um plano $\alpha$ o pé da perpendicular ao plano conduzida pelo ponto. O plano $\alpha$ é chamado de plano de projeção e a reta perpendicular é chamada...
- Demonstração Da Relação Trigonométrica Fundamental
Nesta artigo, veremos como encontrar a relação trigonométrica fundamental no círculo trigonométrico utilizando o teorema de Pitágoras. Considere o círculo trigonométrico abaixo de raio unitário: O ponto $C$ é um ponto genérico sobre a circunferência...
Matemática
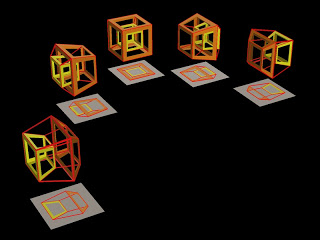
A matemática da Rotação dos cubos

Há duas transformações importantes nesta imagem: rotações e projeções. A idéia de sombra representa-se matematicamente por projeção, que pode ser de duas formas. A primeira é a projeção ortográfica, que corresponde a uma fonte luminosa infinitamente distante. Neste caso a sombra é do tamanho do objecto projetado, independentemente da distância deste à sua sombra. (Esta maneira de projetar está descrita com mais detalhe em Cubos às Fatias - ver nosso post).
A segunda é a projeção estereográfica. Esta corresponde a ter a fonte luminosa a uma distância finita da superfície onde as sombras se formam. Neste caso as sombras dos objetos mais próximos da luz têm sombras maiores do que os que estão mais afastados. Podemos fazer a experiência numa sala escura com uma lâmpada, para ver bem como isto funciona. Matematicamente, a projeção estereográfica a partir do ponto (0,0,0,d) do espaço tetradimensional sobre o hiperplano xyz (isto é, o espaço a três dimensões) é dada pela aplicação
$$p_d: \mathbb{R}^4 \mapsto \mathbb{R}^3$$
e
$$p_d(x,y,z,w) = \frac{d}{d-w}(x,y,z)$$
para todos os pontos onde $$w\ne d$$.
No nosso caso, o objeto projetado é o hipercubo de vértices (±1,±1,±1,±1) e o centro de projeção é o ponto que tem d = 4. Mas o nosso cubo é rodado antes de ser projectado. Uma rotação representa-se por multiplicação por uma matriz, por exemplo, para rodar no espaço tetradimensional de forma a que o eixo dos xx se aproxime do eixo dos ww um ângulo $$\theta$$ podemos usar a função:
$$R_\theta (x,y,z,w) = \begin{pmatrix}\cos\theta & 0& 0& -\sin\theta\\ 0&1&1&0\\ 0&1&1&0\\ \sin\theta & 0& 0&\cos \theta\end{pmatrix} \begin{pmatrix}x\\y\\z\\w\end{pmatrix}.$$
Movendo os vértices do hipercubo através desta rotação seguindo-se a projeção obtemos a posição no espaço tridimensional da sombra do hipercubo.
Para determinar as arestas dos hipercubo, começamos por formar as arestas de um cubo comum tridimensional, depois juntamos uma quarta coordenada, -1. Formamos um segundo cubo e nova quarta coordenada, neste caso 1. (Estes são os cubos amarelo e laranja). Finalmente ligamos os vértices correspondentes nestes dois cubos por intermédio de arestas. Temos então o esqueleto do hipercubo que se pode ver na imagem.
Fonte: Para Além da Terceira Dimensão. -
Fonte: Para Além da Terceira Dimensão. -
- Desafio - Física
Na figura, um bloco sobe um plano inclinado, com velocidade inicial $$V_0$$. Considere $$\mu$$ o coeficiente de atrito entre o bloco e a superfície. Indique sua velocidade ao passar pela posição inicial. A. $$V_0\sqrt{\frac{sen\theta - \mu cos\theta}{sen\theta...
- Tetravista De Z²
As três Tetravistas mostradas na exposição são uma tentativa para entender melhor gráficos de funções complexas. O gráfico duma função de variável complexa está no espaço complexo bidimensional, que pode ser identificado naturalmente com...
- Triângulo De Pascal
O Triângulo de Pascal é um triângulo numérico formado por Binômios de Newton (leia o post sobre binômio de Newton) $$\begin{pmatrix}n\\k\end{pmatrix}$$, onde $$n$$ representa o número da linha (posição vertical) e $$K$$ representa o número da...
- Projeção Ortogonal De Um Segmento De Reta Sobre Um Plano
$1)$ Projeção de um ponto Definição $1$: Chama-se projeção ortogonal de um ponto $P$ sobre um plano $\alpha$ o pé da perpendicular ao plano conduzida pelo ponto. O plano $\alpha$ é chamado de plano de projeção e a reta perpendicular é chamada...
- Demonstração Da Relação Trigonométrica Fundamental
Nesta artigo, veremos como encontrar a relação trigonométrica fundamental no círculo trigonométrico utilizando o teorema de Pitágoras. Considere o círculo trigonométrico abaixo de raio unitário: O ponto $C$ é um ponto genérico sobre a circunferência...
