Matemática
Esta postagem tem o objetivo de relatar algo sobre a interessantíssima história do surgimento dos números complexos.
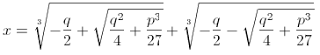
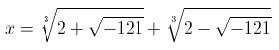
^3=\left%20(2-%20\sqrt{-121}%20\right%20))
^3=\left%20(2+%20\sqrt{-121}%20\right%20))
- História Da Soluções Algébrica Da Equação Do 4º Grau
As equações do terceiro e quarto grau têm suas histórias de soluções algébricas bastante parecidas e que acontecem no mesmo momento, isto é, na Itália do século XVI. A solução algébrica da equação do 4º grau se deu graças ao matemático,...
- Questão 4 ? Professor De Matemática ? Seap ? Paraná? 2.013
O matemático, filósofo e médico Girolamo Cardano (1501?1576) publicou em 1545, na obra de sua autoria nominada de Ars Magna, a fórmula resolutiva de uma equação do terceiro grau que estivesse escrita na forma x3 + px + q =...
- Plano De Argand - Gauss
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...
- Operações Com Números Complexos Na Forma Trigonométrica
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br Operações...
- Números Complexos
Por volta do século XV, os matemáticos tinham um único pensamento: "O quadrado de um número positivo, bem como o de um número negativo, é positivo. Um número negativo não é quadrado de nenhum número, pois não existe raiz quadrada de um número...
Matemática
Alguma coisa sobre o surgimento dos números complexos
Esta postagem tem o objetivo de relatar algo sobre a interessantíssima história do surgimento dos números complexos.
SURGIMENTO
O surgimento dos números complexos está intimamente relacionado ao aparecimento de raízes quadradas de números negativos em algumas expressões matemáticas. Os matemáticos, há muito tempo, sabem resolver equações quadráticas. Hoje em dia usamos uma fórmula bem conhecida e que chamamos (no Brasil) de ?fórmula de Bhascara?.
Os matemáticos do século XVI estavam interessados em encontar uma fórmula para resolver equações cúbicas (equações da forma ax³ + bx² + cx + d = 0). Com uma série de manipulações eles conseguiram simplificar a equação completa para x³ + px + q = 0. Com mais uma série de manipulações eles conseguiram deduzir a seguinte fórmula:
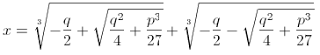
Um problema nesta fórmula apareceu quando o matemático italiano Rafael Bobelli tentou aplicá-la para resolver a equação x³ - 15x - 4 = 0. O resultado que ele obteve foi o seguinte:
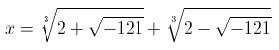
No caso de equações quadráticas, quando aparecia raízes de números negativos eles simplesmente paravam e diziam: não há solução. Mas neste caso era diferente, pois eles sabiam de antemão que 4 era solução!
Este fato poderia levar os matemáticos a pensarem que a fórmula não era tão eficiente e que só funcionava em alguns casos e a abandoná-la por completo, mas em vez disso os levou ao desenvolvimento dos números complexos.
O passo crucial foi dado por Bombelli que fez coisas como
^2=-1)

Ou seja, ele aplicou às "raízes quadradas de números negativos" algumas propriedades que até então só eram aplicada a números inteiros. Fazendo isso ele percebeu que:
Ou seja, ele aplicou às "raízes quadradas de números negativos" algumas propriedades que até então só eram aplicada a números inteiros. Fazendo isso ele percebeu que:
O fato é que substituindo estes resultados na expressão obtida para x ele obteve x = 4 que realmente é uma solução. Foi a partir disto que os matemáticos começaram a tratar as ?raízes quadradas de números negativos? como se fossem números.
PERSONAGENS
O primeiro homem que publicou a fórmula que resolve a equação cúbica foi o italiano Gerônimo Cardano. Por isso a fórmula é conhecida como fórmula de Cardano-Tartaglia. O nome Tartaglia aparece na fórmula devido ao fato de ter sido o italiano Niccolo Tartaglia quem contou a Cardano como resolver a cúbica.
Contudo, o primeiro a fazer a descoberta foi Scipione del Ferro que acabou morrendo sem publicar a descoberta. Antes de morrer, porém, ele revelou a solução para um estudante seu chamado Antonio Maria Fior. Quando se espalhou a notícia de que existia uma fórmula, Tartaglia começou a procurar e acabou conseguindo encontar um modo de resolver a cúbica (não se sabe se sozinho ou se alguém lhe contou como fazer).
Quando a notícia de que Tartaglia sabia resolver a cúbica se espalhou foi organizada uma competição entre ele e Fior. Cada um propôs 30 questões ao outro. Tartaglia saiu vitorioso (resolvendo todas as questões) e Fior perdeu feio (não resolveu nenhuma das questões que Tartaglia propôs).
Cardano (médico de sucesso) convenceu Tartaglia (homem sem recursos) a lhe contar a solução, jurando segredo. Cardano descumpriu a promessa e publicou a fórmula em sua obra Ars Magna acabando assim com o sonho de Tartaglia - que pretendia publicar este importante resultado para a época firmando assim sua reputação.
ACEITAÇÃO
A princípio, a surgimento dos números complexos causou perplexidade nos matemáticos. Na época até mesmo os números negativos eram vistos com desconfiança. Uma raiz quadrada de número negativo era coisa ainda mais absurda. Foi o que levou Cardano dizer coisas como ?um resultado tão sutil quanto inútil? com relação à sua fórmula que produzia raiz de números negativos ou ?esqueça a tortura mental que isto significa e vá operando? com relação à tratar esta coisa (que hoje chamamos de unidade imaginária) como número.
A coisa mudou de figura quando descobriram uma interpretação geométrica para os números complexos. Eles começaram a representar os números complexos em um plano. Assim eles podiam ?ver? os números complexos. O primeiro que usou uma tal representação foi o matemático norueguês Caspar Wessel publicada em 1798. Cerca de 15 anos mais tarde a ideia se tornou amplamente aceita após ter sido usada por Gauss. Hoje o plano em que se representa estes números é conhecido como Plano de Argand-Gauss em homenagem a Gauss e a Jean-Robert Argand - um matemático nascido na suiça que também usou uma representação geométrica (antes da publicação de Gauss).
Se o leitor conhecer uma versão um pouco diferente desta história ou se quiser acrescentar algum detalhe que foi omitido deixe nos comentários.
Veja aqui um interessante problema de geometria cuja solução pode ser achada utilizando números complexos.
Veja aqui um interessante problema de geometria cuja solução pode ser achada utilizando números complexos.
Referências: A Emergência dos Números Complexos; A Geometria e o Ensino dos Números Complexos; A Equação do Terceiro Grau. (ou aqui).
Erros podem ser relatados aqui.
- História Da Soluções Algébrica Da Equação Do 4º Grau
As equações do terceiro e quarto grau têm suas histórias de soluções algébricas bastante parecidas e que acontecem no mesmo momento, isto é, na Itália do século XVI. A solução algébrica da equação do 4º grau se deu graças ao matemático,...
- Questão 4 ? Professor De Matemática ? Seap ? Paraná? 2.013
O matemático, filósofo e médico Girolamo Cardano (1501?1576) publicou em 1545, na obra de sua autoria nominada de Ars Magna, a fórmula resolutiva de uma equação do terceiro grau que estivesse escrita na forma x3 + px + q =...
- Plano De Argand - Gauss
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br ...
- Operações Com Números Complexos Na Forma Trigonométrica
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br Operações...
- Números Complexos
Por volta do século XV, os matemáticos tinham um único pensamento: "O quadrado de um número positivo, bem como o de um número negativo, é positivo. Um número negativo não é quadrado de nenhum número, pois não existe raiz quadrada de um número...
