Matemática
Vejam mais:
Como Encontrar o Centro de uma Circunferência
Teorema de Pitágoras Segundo Euclides
Algoritmo de Euclides para Determinação do MDC

- A Reta De Euler
Quando falamos em Euler e os resultados obtidos pelo mesmo não deixamos de nos surpreender com as descobertas desse gênio da matemática, o mesmo contribuiu com a geometria plana, e ele notou que em um triângulo qualquer o Ortocentro (Encontro das...
- Teorema Do Quadrilátero Circunscritível
Este artigo trata do quadrilátero circunscrito a uma circunferência. Veremos a condição necessária e suficiente, algumas propriedades e teoremas interessantes e alguns exercícios resolvidos. Teorema $1$:Se conduzirmos por um ponto $P$ os segmentos...
- Construção De Um Pentágono Regular Com Régua E Compasso (parte 4) - Método De Hirano
Esta é uma elegante construção do pentágono regular pelos métodos euclidianos, elaborado por Yoshifusa Hirano. A construção foi incluída num manuscrito Sanpo Jyojutu Kaigi, por Chorin Kawakita $(1840-1919)$ que escreveu:"Hirano descobriu...
- Construção De Um Pentágono (quase) Regular Com Régua E Compasso - Parte $1$
Esta é a primeira construção de um pentágono usando régua e compasso. Apesar de tê-la encontrada como sendo um pentágono regular, mostrou-se, por fim, que é apenas uma ótima aproximação, tendo os ângulos internos diferenças menores que $1$...
- Demonstração Da Relação Trigonométrica Fundamental
Nesta artigo, veremos como encontrar a relação trigonométrica fundamental no círculo trigonométrico utilizando o teorema de Pitágoras. Considere o círculo trigonométrico abaixo de raio unitário: O ponto $C$ é um ponto genérico sobre a circunferência...
Matemática
Como Achar o Centro do Círculo, por Euclides
No livro $III$ dos Elementos, Proposição $1$, Euclides nos mostra como achar o centro de um círculo dado de maneira muito elementar e elegante.
Proposição $1$ do Livro $III$: Achar o centro do círculo dado.
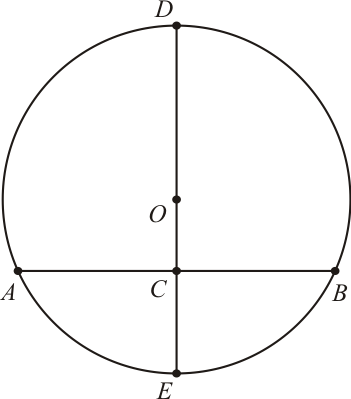
Seja o círculo $C_1$. Tracemos através dele uma corda $\overline{AB}$ ao acaso. Tracemos sua mediatriz, marcando os pontos $C$, $D$ e $E$. O ponto médio do segmento $\overline{DE}$ é o centro $O$ do círculo $C_1$.
[Figura 1]
Para a demonstração, Euclides inicia com o absurdo de que um ponto genérico $G$ no interior do círculo seja seu centro.
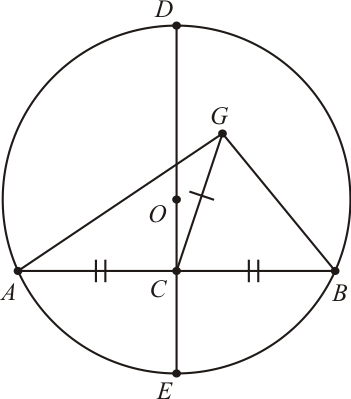
Tracemos uma corda $\overline{AB}$ ao acaso e sua mediatriz, marcando os pontos $C$, $D$ e $E$. Tomemos o ponto genérico $G$ como centro. Se $G$ é o centro do círculo, então tracemos os segmentos $\overline{GA}$, $\overline{GC}$ e $\overline{GB}$.

[Figura 2]
Como $\overline{AC}$ é igual a $\overline{BC}$ e $\overline{GC}$ é comum aos triângulos $ACG$ e $BCG$, então os segmentos $\overline{AC}$ e $\overline{GC}$ são iguais aos segmentos $\overline{BC}$ e $\overline{GC}$, respectivamente.
Se $G$ é o centro do círculo, então $\overline{GA}=\overline{GB}$, pois são os raios do círculo. Portanto, o ângulo $A\hat{C}G$ é igual ao ângulo $B\hat{C}G$, que são retos, já que a mediatriz $\overline{DE}$ define ângulos retos com a corda $\overline{AB}$. Mas por construção, o ângulo $O\hat{C}B$ também é reto, assim como o ângulo $G\hat{C}B$. Mas $G\hat{C}B$ é menor que $O\hat{C}B$, o que torna impossível ser o ponto $G$ o centro do círculo, exceto se este estiver sobre a mediatriz $\overline{DE}$. Assim, o ponto $O$ é o centro da círculo $C_1$.
Em outro artigo deste blog, sobre Como Encontrar o Centro de uma Circunferência, utilizamos $3$ pontos sobre uma circunferência $A$, $B$ e $C$ e traçamos as mediatrizes das cordas $\overline{AB}$ e $\overline{BC}$. O ponto de encontro dessas mediatrizes define o centro $O$ da circunferência.
Vejam que esse método é essencialmente o método que Euclides utilizou em seu Elementos. Se fizermos coincidir os pontos $E$ com $B$, basta construirmos as mediatrizes das cordas $\overline{AB}$ e $\overline{BD}$. A intersecção cairá sobre o centro $O$ do círculo.
Referências:
[1] Os Elementos - Euclides - Tradução de Irineu Bicudo - Ed. Unesp
Vejam mais:
Como Encontrar o Centro de uma Circunferência
Teorema de Pitágoras Segundo Euclides
Algoritmo de Euclides para Determinação do MDC

- A Reta De Euler
Quando falamos em Euler e os resultados obtidos pelo mesmo não deixamos de nos surpreender com as descobertas desse gênio da matemática, o mesmo contribuiu com a geometria plana, e ele notou que em um triângulo qualquer o Ortocentro (Encontro das...
- Teorema Do Quadrilátero Circunscritível
Este artigo trata do quadrilátero circunscrito a uma circunferência. Veremos a condição necessária e suficiente, algumas propriedades e teoremas interessantes e alguns exercícios resolvidos. Teorema $1$:Se conduzirmos por um ponto $P$ os segmentos...
- Construção De Um Pentágono Regular Com Régua E Compasso (parte 4) - Método De Hirano
Esta é uma elegante construção do pentágono regular pelos métodos euclidianos, elaborado por Yoshifusa Hirano. A construção foi incluída num manuscrito Sanpo Jyojutu Kaigi, por Chorin Kawakita $(1840-1919)$ que escreveu:"Hirano descobriu...
- Construção De Um Pentágono (quase) Regular Com Régua E Compasso - Parte $1$
Esta é a primeira construção de um pentágono usando régua e compasso. Apesar de tê-la encontrada como sendo um pentágono regular, mostrou-se, por fim, que é apenas uma ótima aproximação, tendo os ângulos internos diferenças menores que $1$...
- Demonstração Da Relação Trigonométrica Fundamental
Nesta artigo, veremos como encontrar a relação trigonométrica fundamental no círculo trigonométrico utilizando o teorema de Pitágoras. Considere o círculo trigonométrico abaixo de raio unitário: O ponto $C$ é um ponto genérico sobre a circunferência...
