Matemática
O Heptágono regular foi fonte de muito mistério na Geometria, quanto à sua construção com régua e compasso, apenas.
Gaus provou aos $19$ anos que o heptadecágono regular é construtível com régua e compasso. De seus estudos sobre a contrutibilidade de $p-\text{ágonos}$ regulares, ou seja, polígonos de $p$ lados, sendo $p$ um número primo, descobriu que são construtíveis se, e somente se, $p$ é um número de Fermat:
\begin{equation*}
\Large p = 2^{n^n}+1
\end{equation*}
Suas análises aparecem na obra: Disquisitiones Arithmeticae.
Como $7$ não é um número primo de Fermat, a construção de um heptágono regular é impossível utilizando régua e compasso. A construção que segue é apenas uma boa aproximação, mas dependendo da aplicação, pode ser tomada como satisfatória.

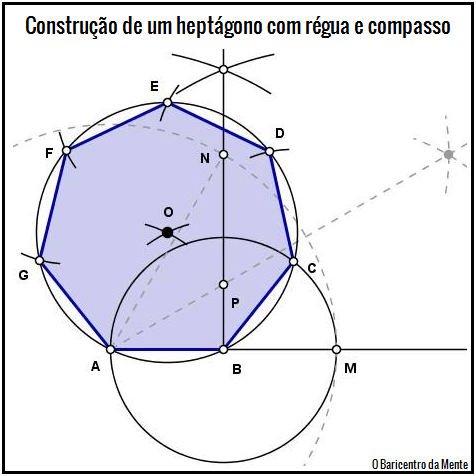
$2)$ Com centro em $B$ e raio $BA$, descreva a circunferência e marque como $M$ a intresecção com o prolongamento de $AB$:

$3)$ Suba a perpendicular em $B$:

$4)$ Com centro em $A$ e raio $AM$, descreva o arco e marque como $N$ a intersecção com a perpendicular:

$5)$ Trace a bissetriz interna do arco $MN$ e marque como $P$ a intersecção com a perpendicular:

$6)$ Agora, descreva dois arcos: o primeiro com centro em $A$ e raio $AP$ e o segundo com centro em $B$ e raio $AP$. A intersecção desses arcos marque como $O$, que será o centro da circunferência circunscrita ao heptágono:

$7)$ Com centro em $O$ descreva a circunferência de raio $AO$ e marque como $C$ a intersecção com a primeira circunferência. Vejam que já obtivemos dois lados do heptágono:

$8)$ Com raio $AB$ descreve arcos sobre a circunferência que circunscreve o heptágono, primeiro com centro em $C$ e marque o ponto $D$ na intersecção com a circunferência; depois com centro em $D$ marque como $E$ a intersecção com a circunferência; e assim até formar os $7$ lados, obtendo o heptágono circunscrito a partir do lado:

Construção de um heptágono regular com régua e compasso (Parte 2)
Construção de um heptadecágono regular com régua e compasso
Construções geométricas utilizando régua e compasso

- Construção De Um Pentágono Regular Com Régua E Compasso (parte 4) - Método De Hirano
Esta é uma elegante construção do pentágono regular pelos métodos euclidianos, elaborado por Yoshifusa Hirano. A construção foi incluída num manuscrito Sanpo Jyojutu Kaigi, por Chorin Kawakita $(1840-1919)$ que escreveu:"Hirano descobriu...
- Construção De Um Heptágono Regular Com Régua E Compasso (parte Ii)
Já vimos como construir uma aproximação para o heptágono regular a partir do lado. Vamos aqui construir uma aproximação do heptágono a partir da circunferência circunscrita. 1) Inicie com uma circunferência de centro O: 2) Trace o diâmetro...
- Construção De Um Decágono Regular Com Régua E Compasso
Esta construção foi elaborada por mim quando estava brincando com o software Régua e Compasso. Provavelmente não seja inédita, mas não encontrei nenhuma fonte que mostre tal construção. Para esta construção, inicie com uma circunferência C1...
- Construção De Um Pentágono Regular Com Régua E Compasso (parte Iii)
Neste post vou mostrar uma terceira maneira de construir um pentágono regular utilizando régua e compasso. Para ver as construções anteriores, clique em Parte I e Parte II. Para esta construção, comece traçando um segmento de reta AB que será...
- Construção De Um Pentágono (quase) Regular Com Régua E Compasso - Parte $1$
Esta é a primeira construção de um pentágono usando régua e compasso. Apesar de tê-la encontrada como sendo um pentágono regular, mostrou-se, por fim, que é apenas uma ótima aproximação, tendo os ângulos internos diferenças menores que $1$...
Matemática
Construção de um heptágono regular com régua e compasso (Parte 1)
O Heptágono regular foi fonte de muito mistério na Geometria, quanto à sua construção com régua e compasso, apenas.

Gaus provou aos $19$ anos que o heptadecágono regular é construtível com régua e compasso. De seus estudos sobre a contrutibilidade de $p-\text{ágonos}$ regulares, ou seja, polígonos de $p$ lados, sendo $p$ um número primo, descobriu que são construtíveis se, e somente se, $p$ é um número de Fermat:
\begin{equation*}
\Large p = 2^{n^n}+1
\end{equation*}
Suas análises aparecem na obra: Disquisitiones Arithmeticae.
Como $7$ não é um número primo de Fermat, a construção de um heptágono regular é impossível utilizando régua e compasso. A construção que segue é apenas uma boa aproximação, mas dependendo da aplicação, pode ser tomada como satisfatória.
Construção:
$1)$ Trace o segmento $AB$ prolongando-o no sentido de $B$:
$2)$ Com centro em $B$ e raio $BA$, descreva a circunferência e marque como $M$ a intresecção com o prolongamento de $AB$:

$3)$ Suba a perpendicular em $B$:

$4)$ Com centro em $A$ e raio $AM$, descreva o arco e marque como $N$ a intersecção com a perpendicular:

$5)$ Trace a bissetriz interna do arco $MN$ e marque como $P$ a intersecção com a perpendicular:

$6)$ Agora, descreva dois arcos: o primeiro com centro em $A$ e raio $AP$ e o segundo com centro em $B$ e raio $AP$. A intersecção desses arcos marque como $O$, que será o centro da circunferência circunscrita ao heptágono:

$7)$ Com centro em $O$ descreva a circunferência de raio $AO$ e marque como $C$ a intersecção com a primeira circunferência. Vejam que já obtivemos dois lados do heptágono:

$8)$ Com raio $AB$ descreve arcos sobre a circunferência que circunscreve o heptágono, primeiro com centro em $C$ e marque o ponto $D$ na intersecção com a circunferência; depois com centro em $D$ marque como $E$ a intersecção com a circunferência; e assim até formar os $7$ lados, obtendo o heptágono circunscrito a partir do lado:

Veja mais:
Construção de um heptágono regular com régua e compasso (Parte 2)
Construção de um heptadecágono regular com régua e compasso
Construções geométricas utilizando régua e compasso

- Construção De Um Pentágono Regular Com Régua E Compasso (parte 4) - Método De Hirano
Esta é uma elegante construção do pentágono regular pelos métodos euclidianos, elaborado por Yoshifusa Hirano. A construção foi incluída num manuscrito Sanpo Jyojutu Kaigi, por Chorin Kawakita $(1840-1919)$ que escreveu:"Hirano descobriu...
- Construção De Um Heptágono Regular Com Régua E Compasso (parte Ii)
Já vimos como construir uma aproximação para o heptágono regular a partir do lado. Vamos aqui construir uma aproximação do heptágono a partir da circunferência circunscrita. 1) Inicie com uma circunferência de centro O: 2) Trace o diâmetro...
- Construção De Um Decágono Regular Com Régua E Compasso
Esta construção foi elaborada por mim quando estava brincando com o software Régua e Compasso. Provavelmente não seja inédita, mas não encontrei nenhuma fonte que mostre tal construção. Para esta construção, inicie com uma circunferência C1...
- Construção De Um Pentágono Regular Com Régua E Compasso (parte Iii)
Neste post vou mostrar uma terceira maneira de construir um pentágono regular utilizando régua e compasso. Para ver as construções anteriores, clique em Parte I e Parte II. Para esta construção, comece traçando um segmento de reta AB que será...
- Construção De Um Pentágono (quase) Regular Com Régua E Compasso - Parte $1$
Esta é a primeira construção de um pentágono usando régua e compasso. Apesar de tê-la encontrada como sendo um pentágono regular, mostrou-se, por fim, que é apenas uma ótima aproximação, tendo os ângulos internos diferenças menores que $1$...
