Matemática
Veremos nesta postagem como determinar os pontos de máximo e mínimo de uma função de segundo grau.
\begin{equation*}
f(x) = ax^2 + \frac{ab}{a}x + \frac{ac}{a}
\end{equation*}
Colocando $a$ em evidência:
\begin{equation*}
f(x) = a\left[ x^2 + \frac{b}{a}x + \frac{c}{a} \right]
\end{equation*}
Se somarmos e subtrairmos um mesmo valor arbitrário de uma função, a mesma não sofrerá alteração em seu valor final. Utilizaremos um valor conveniente igual a $\displaystyle \frac{b^2}{4a^2}$:
\begin{equation*}
f(x) = a\left[x^2 + \frac{b}{a}x + \frac{b^2}{4a^2} - \frac{b^2}{4a^2} + \frac{c}{a} \right]\\
\ \\
f(x) = a\left[ \left( x^2+\frac{b}{a}x + \frac{b^2}{4a^2}\right) - \left(\frac{b^2}{4a^2}-\frac{c}{a}\right) \right]\\
\ \\
f(x) = a\left[\left(x+\frac{b}{2a}\right)^2 - \left(\frac{b^2-4ac}{4a^2}\right) \right]
\end{equation*}
Representamos $b^2-4ac$ por $\Delta$, que é o discriminante do triômio do segundo grau:
\begin{equation*}
f(x) = a\left[ \left(x+\frac{b}{2a}\right)^2 - \left(\frac{\Delta}{4a^2}\right)\right]
\end{equation*}
Temos então que:
\begin{equation}
y = a\left[\left(x+\frac{b}{2a}\right)^2 - \left(\frac{\Delta}{4a^2}\right)\right]
\end{equation}
Se analisarmos a equação $(1)$ mais minuciosamente, podemos concluir que, se $a<0$, o valor de $y$ será tanto maior quanto menor for o valor da diferença:
\begin{equation}
\left(x+\frac{b}{2a}\right)^2 - \left(\frac{\Delta}{4a^2}\right)
\end{equation}
E dessa diferença dada em $(2)$, podemos concluir que:
$\bullet$ O valor $\displaystyle -\frac{\Delta}{4a^2}$ é constante, pois não depende da variável $x$, somente dos coeficientes $a$, $b$ e $c$.
$\bullet$ O valor $\displaystyle \left( x+\frac{b}{2a}\right)^2 \geq0,\ \forall \ x \in \mathbb{R}$, já que para quaisquer valores assumidos por $x$, $a$ e $b$, $\displaystyle \left(x+\frac{b}{2a}\right)^2$ nunca será negativo, pois está elevado ao quadrado.
Reescrevemos a diferença dada em $(2)$ como:
\begin{equation}
\left(x+\frac{b}{2a}\right)^2 - \frac{\Delta}{4a^2} = (x+M)^2 - k
\end{equation}
Atribuindo valores para $x$ de modo a averiguar para quais valores assumidos por $x$ leva a diferença $(3)$ ao menor valor possível:
Se $x = -M$, então $(-M+M)^2 - k = 0-k = -k$.
Se $x=1-M$, então $(1-M+M)^2 - k = 1-k$.
Se $x=2-M$, então $(2-M+M)^2 - k = 4-k$.
Se $x=-3-M$, então $(-3-M+M)^2 - k = 9-k$
Podemos notar que para qualquer valor diferente de $-M$ assumido por $x$, a diferença $(3)$ aumenta. Portanto, essa diferença assume o menor valor possível quando $\displaystyle \left(x+\frac{b}{2a}\right)^2=0$, ou seja, quando $\displaystyle -\frac{b}{2a}$. Então:
\begin{equation*}
y = a\left[ \left(-\frac{b}{2a}+\frac{b}{2a}\right)^2 - \frac{\Delta}{4a^2}\right]\\
\ \\
y = a\left(0^2 - \frac{\Delta}{4a^2}\right)\\
\ \\
y = -\frac{\Delta}{4a}
\end{equation*}
Então, as coordenadas do vértice da parábola são:
\begin{equation*}
x = -\frac{b}{2a} \qquad \text{e} \qquad y=-\frac{\Delta}{4a}
\end{equation*}
Método de resolução das equações de Sebá
Resolvendo equações quadráticas pelo método geométrico de Descartes

- Resolução Da Integral $\displaystyle \int \frac{x^2+1}{x^2-1}dx$
Nesta postagem, veremos que: \begin{equation*} \int \frac{x^2+1}{x^2-1}dx = x+ \ln|x-1|- \ln|x+1| + C \end{equation*} onde $x \in \mathbb{R}$, sendo $x \neq \pm 1$. Seja a integral: \begin{equation*} I = \int \frac{x^2+1}{x^2-1}dx \end{equation*} Decompomos...
- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a^2}dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a^2}\ dx = \frac{1}{a}\text{arctg}\left(\frac{x}{a}\right) + C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2 + a^2 \neq 0$. Seja a integral:...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
Matemática
Demonstração dos pontos de Máximo e Mínimo de uma Função Quadrática
Veremos nesta postagem como determinar os pontos de máximo e mínimo de uma função de segundo grau.

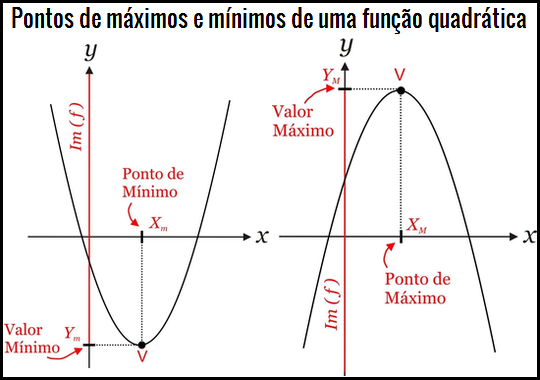
Definição $1$: Valor de máximo
Dizemos que o número $Y_M \in Im(f)$ é o valor de máximo da função $y=f(x)$ se, e somente se, $Y_M \geq y$, $\forall\ y \in Im(f)$. O número $Y_M \in D(f)$, tal que $Y_M=f(X_M)$ é chamado de ponto de máximo da função.Definição $2$: Valor de mínimo
Dizemos que o número $Y_m \in Im(f)$ é o valor de mínimo da função $y=f(x)$ se, e somente se, $Y_m \leq y$, $\forall\ y \in Im(f)$. O número $Y_m \in D(f)$, tal que $Y_m=f(X_m)$ é chamado de ponto de mínimo da função.Teorema $1$
Se $a<0$, a função quadrática $y=ax^2+bx+c$ admite o valor máximo $\displaystyle Y_M=-\frac{\Delta}{4a}$ para $\displaystyle X_M = -\frac{b}{2a}$.Teorema $2$
Se $a>0$, a função quadrática $y=ax^2+bx+c$ admite o valor mínimo $\displaystyle Y_m=-\frac{\Delta}{4a}$ para $\displaystyle X_m=-\frac{b}{2a}$.Demonstração
Para esta demonstração, vamos primeiramente transformar a função quadrática $y=f(x)=ax^2+bx+c$ em sua forma canônica. Iniciamos reescrevendo-a na seguinte forma:\begin{equation*}
f(x) = ax^2 + \frac{ab}{a}x + \frac{ac}{a}
\end{equation*}
Colocando $a$ em evidência:
\begin{equation*}
f(x) = a\left[ x^2 + \frac{b}{a}x + \frac{c}{a} \right]
\end{equation*}
Se somarmos e subtrairmos um mesmo valor arbitrário de uma função, a mesma não sofrerá alteração em seu valor final. Utilizaremos um valor conveniente igual a $\displaystyle \frac{b^2}{4a^2}$:
\begin{equation*}
f(x) = a\left[x^2 + \frac{b}{a}x + \frac{b^2}{4a^2} - \frac{b^2}{4a^2} + \frac{c}{a} \right]\\
\ \\
f(x) = a\left[ \left( x^2+\frac{b}{a}x + \frac{b^2}{4a^2}\right) - \left(\frac{b^2}{4a^2}-\frac{c}{a}\right) \right]\\
\ \\
f(x) = a\left[\left(x+\frac{b}{2a}\right)^2 - \left(\frac{b^2-4ac}{4a^2}\right) \right]
\end{equation*}
Representamos $b^2-4ac$ por $\Delta$, que é o discriminante do triômio do segundo grau:
\begin{equation*}
f(x) = a\left[ \left(x+\frac{b}{2a}\right)^2 - \left(\frac{\Delta}{4a^2}\right)\right]
\end{equation*}
Temos então que:
\begin{equation}
y = a\left[\left(x+\frac{b}{2a}\right)^2 - \left(\frac{\Delta}{4a^2}\right)\right]
\end{equation}
Se analisarmos a equação $(1)$ mais minuciosamente, podemos concluir que, se $a<0$, o valor de $y$ será tanto maior quanto menor for o valor da diferença:
\begin{equation}
\left(x+\frac{b}{2a}\right)^2 - \left(\frac{\Delta}{4a^2}\right)
\end{equation}
E dessa diferença dada em $(2)$, podemos concluir que:
$\bullet$ O valor $\displaystyle -\frac{\Delta}{4a^2}$ é constante, pois não depende da variável $x$, somente dos coeficientes $a$, $b$ e $c$.
$\bullet$ O valor $\displaystyle \left( x+\frac{b}{2a}\right)^2 \geq0,\ \forall \ x \in \mathbb{R}$, já que para quaisquer valores assumidos por $x$, $a$ e $b$, $\displaystyle \left(x+\frac{b}{2a}\right)^2$ nunca será negativo, pois está elevado ao quadrado.
Reescrevemos a diferença dada em $(2)$ como:
\begin{equation}
\left(x+\frac{b}{2a}\right)^2 - \frac{\Delta}{4a^2} = (x+M)^2 - k
\end{equation}
Atribuindo valores para $x$ de modo a averiguar para quais valores assumidos por $x$ leva a diferença $(3)$ ao menor valor possível:
Se $x = -M$, então $(-M+M)^2 - k = 0-k = -k$.
Se $x=1-M$, então $(1-M+M)^2 - k = 1-k$.
Se $x=2-M$, então $(2-M+M)^2 - k = 4-k$.
Se $x=-3-M$, então $(-3-M+M)^2 - k = 9-k$
Podemos notar que para qualquer valor diferente de $-M$ assumido por $x$, a diferença $(3)$ aumenta. Portanto, essa diferença assume o menor valor possível quando $\displaystyle \left(x+\frac{b}{2a}\right)^2=0$, ou seja, quando $\displaystyle -\frac{b}{2a}$. Então:
\begin{equation*}
y = a\left[ \left(-\frac{b}{2a}+\frac{b}{2a}\right)^2 - \frac{\Delta}{4a^2}\right]\\
\ \\
y = a\left(0^2 - \frac{\Delta}{4a^2}\right)\\
\ \\
y = -\frac{\Delta}{4a}
\end{equation*}
Então, as coordenadas do vértice da parábola são:
\begin{equation*}
x = -\frac{b}{2a} \qquad \text{e} \qquad y=-\frac{\Delta}{4a}
\end{equation*}
Referências:
[1] Fundamentos de Matemática Elementar V1 - Gelson IezziVeja mais:
Completando o quadradoMétodo de resolução das equações de Sebá
Resolvendo equações quadráticas pelo método geométrico de Descartes

- Resolução Da Integral $\displaystyle \int \frac{x^2+1}{x^2-1}dx$
Nesta postagem, veremos que: \begin{equation*} \int \frac{x^2+1}{x^2-1}dx = x+ \ln|x-1|- \ln|x+1| + C \end{equation*} onde $x \in \mathbb{R}$, sendo $x \neq \pm 1$. Seja a integral: \begin{equation*} I = \int \frac{x^2+1}{x^2-1}dx \end{equation*} Decompomos...
- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a^2}dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a^2}\ dx = \frac{1}{a}\text{arctg}\left(\frac{x}{a}\right) + C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2 + a^2 \neq 0$. Seja a integral:...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Resolução Da Integral $\int \cos(x) \cos(2x)dx$
Para a resolução desta integral, usaremos a técnica de integração por substituição e usaremos uma identidade trigonométrica que transforma um produto de cossenos em soma. Seja a integral: \begin{equation} \int \cos(2x) \cos(x) dx \end{equation}...
