Matemática
Podemos argumentar utilizando a relação existente entre a implicação lógica e a teoria (ingênua) dos conjuntos (conforme observação contida aqui):
Sejam A e B dois conjuntos, definidos como se seguem:
- Algumas Curiosidades Lógicas
Nesta postagem não há tema novo algum. Tudo aqui se refere a assuntos muito conhecidos na literatura especializada. No entanto, como vejo inúmeros discursos e textos de matemática no Brasil que fazem consideráveis confusões de caráter lógico,...
- Provando Um Limite [dúvida De Um Leitor]
A pedido de um leitor, nesta postagem apresento solução para um problema envolvendo a noção de limite. O enunciado pede para provar a seguinte igualdade: $$ \lim_{x \rightarrow 1} \frac{x^2}{3x - 4} = -1$$ De acordo com a definição...
- Dúvida Do Leitor [sobre Limites]
Esta postagem tem o intuito de (tentar) responder a dúvida de um leitor. Em comentário publicado aqui, aparentemente ele pede para que usemos a definição formal de limite para provar o seguinte resultado:Notemos, inicialmente, que este...
- O Algoritmo Da Divisão Parte Iii
Nesta série de postagens estamos demonstrando o algoritmo da divisão: Se aé um número inteiro qualquer e bé um número inteiro maior do que zero, então existem dois números inteiros qe rtais que a= bq+ r, onde 0 ? r < b. Além disso, qe rsão...
- Demonstrações De Teoremas Sobre Limites [parte I]
Geralmente, quando nos deparamos com limites como os exemplos que se seguem, não temos dificuldades em resolvê-los: É comum adotarmos o procedimento da substituição direta, ou seja, apenas trocamos o x na função pelo...
Matemática
Demonstrações de teoremas sobre limites [2]
Teorema 4: Se c e b são números reais quaisquer, então 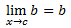 |
O teorema acima é o Teorema 1 no caso em que m = 0. Uma vez que na demonstração do Teorema 1 dividimos por m (por isso exigiu-se m ? 0 no enunciado) aquela demonstração não vale para este caso.
Para demonstrar o Teorema 4, temos que mostrar que para todo ? > 0 existe um ? > 0 tal que
0 < |x ? c| < ? ? |b ? b| < ?
Observe que |b ? b| = 0, portanto, temos que provar, apenas, que para todo ? > 0 existe um ? > 0 tal que
0 < |x ? c| < ? ? 0 < ?
Pergunta: quando é que a implicação acima é satisfeita? Em outras palavras: para quais valores de ?, |x ? c| < ? implica que zero é menor do que ??
Resposta: para qualquer valor positivo.
Conclusão: o ? existe (e é igual a qualquer número positivo) e, portanto, o teorema está demonstrado.
Mas porque qualquer ? > 0 satisfaz a implicação 0 < |x ? c| < ? ? 0 < ??A = {x tal que 0 < |x ? c| < ?}
B = {x tal que |f(x) ? L| < ?}
No caso do Teorema 4 temos f(x) = b e L = b e, portanto, B = ?, para qualquer que seja ? > 0, ou seja, todos os números reais satisfazem |f(x) ? L| < ?. Segue desta observação que desde que ? for positivo (pois a definição de limite exige isso) teremos A ? B (pois uma vez que B tem todos os números reais como seus elementos, não existe x pertencente a A que não pertença a B). Dizer que esta inclusão é válida é equivalente a dizer que 0 < |x ? c| < ? implica 0 < ?.
As demonstrações continuam na próxima postagem da série.
Referências: Livros de Cálculo.
Erros podem ser apontados aqui.
- Algumas Curiosidades Lógicas
Nesta postagem não há tema novo algum. Tudo aqui se refere a assuntos muito conhecidos na literatura especializada. No entanto, como vejo inúmeros discursos e textos de matemática no Brasil que fazem consideráveis confusões de caráter lógico,...
- Provando Um Limite [dúvida De Um Leitor]
A pedido de um leitor, nesta postagem apresento solução para um problema envolvendo a noção de limite. O enunciado pede para provar a seguinte igualdade: $$ \lim_{x \rightarrow 1} \frac{x^2}{3x - 4} = -1$$ De acordo com a definição...
- Dúvida Do Leitor [sobre Limites]
Esta postagem tem o intuito de (tentar) responder a dúvida de um leitor. Em comentário publicado aqui, aparentemente ele pede para que usemos a definição formal de limite para provar o seguinte resultado:Notemos, inicialmente, que este...
- O Algoritmo Da Divisão Parte Iii
Nesta série de postagens estamos demonstrando o algoritmo da divisão: Se aé um número inteiro qualquer e bé um número inteiro maior do que zero, então existem dois números inteiros qe rtais que a= bq+ r, onde 0 ? r < b. Além disso, qe rsão...
- Demonstrações De Teoremas Sobre Limites [parte I]
Geralmente, quando nos deparamos com limites como os exemplos que se seguem, não temos dificuldades em resolvê-los: É comum adotarmos o procedimento da substituição direta, ou seja, apenas trocamos o x na função pelo...
