Matemática
Esta postagem tem o intuito de (tentar) responder a dúvida de um leitor. Em comentário publicado aqui, aparentemente ele pede para que usemos a definição formal de limite para provar o seguinte resultado: Notemos, inicialmente, que este limite poderia ser facilmente calculado pelos teoremas já demonstrados no BLOG MANTHANO (pois esta função é justamente o Teorema 1 no caso em que m = 1 e b = 4/3).
Notemos, inicialmente, que este limite poderia ser facilmente calculado pelos teoremas já demonstrados no BLOG MANTHANO (pois esta função é justamente o Teorema 1 no caso em que m = 1 e b = 4/3).
Mas supondo que não conheçamos este teorema, vejamos (através de um gráfico) que realmente faz sentido querer demonstrar a veracidade desta afirmação:
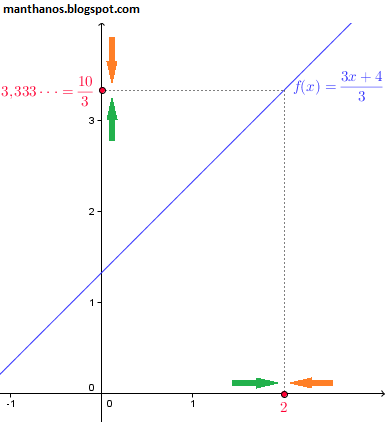 Da figura acima, fica claro que conforme o valor de x se aproxima de 2 o valor de f(x) se aproxima de 10/3.
Da figura acima, fica claro que conforme o valor de x se aproxima de 2 o valor de f(x) se aproxima de 10/3.
Vamos, em fim, para a demonstração:
De acordo com a definição formal, estamos interessado em mostrar que dado qualquer ? > 0 existe um ? > 0 que torna a seguinte implicação válida:

- Provando Um Limite [dúvida De Um Leitor]
A pedido de um leitor, nesta postagem apresento solução para um problema envolvendo a noção de limite. O enunciado pede para provar a seguinte igualdade: $$ \lim_{x \rightarrow 1} \frac{x^2}{3x - 4} = -1$$ De acordo com a definição...
- O Algoritmo Da Divisão Parte Iii
Nesta série de postagens estamos demonstrando o algoritmo da divisão: Se aé um número inteiro qualquer e bé um número inteiro maior do que zero, então existem dois números inteiros qe rtais que a= bq+ r, onde 0 ? r < b. Além disso, qe rsão...
- Demonstrações De Teoremas Sobre Limites [2]
Teorema 4: Se c e b são números reais quaisquer, então O teorema acima é o Teorema 1 no caso em que m = 0. Uma vez que na demonstração do Teorema 1 dividimos por m (por isso exigiu-se m ? 0 no enunciado) aquela demonstração não vale...
- Demonstrações De Teoremas Sobre Limites [parte I]
Geralmente, quando nos deparamos com limites como os exemplos que se seguem, não temos dificuldades em resolvê-los: É comum adotarmos o procedimento da substituição direta, ou seja, apenas trocamos o x na função pelo...
- Sobre A Definição Formal De Limite
O conceito de limite, embora usualmente seja estudado no nível superior, está presente em alguns pontos estudados no nível básico, como por exemplo no caso da dedução da fórmula que fornece a soma dos infinitos termos de uma PG. O conceito...
Matemática
Dúvida do Leitor [sobre limites]
Esta postagem tem o intuito de (tentar) responder a dúvida de um leitor. Em comentário publicado aqui, aparentemente ele pede para que usemos a definição formal de limite para provar o seguinte resultado:
Mas supondo que não conheçamos este teorema, vejamos (através de um gráfico) que realmente faz sentido querer demonstrar a veracidade desta afirmação:

Vamos, em fim, para a demonstração:
De acordo com a definição formal, estamos interessado em mostrar que dado qualquer ? > 0 existe um ? > 0 que torna a seguinte implicação válida:
Mas observe que:

Portanto, a implicação que estamos querendo demonstrar se reduz na seguinte:

Pergunta: para quais valores de ? a implicação acima é verdadeira?
Resposta: para qualquer valor positivo menor do que ou igual a ?.
Conclusão o ? existe e pode ser igual a qualquer número pertencente ao intervalo (0, ?].
Fica assim demonstrado que você pode tornar a diferença entre (3x + 4)/3 e 10/3 tão pequena quanto você quiser. Tudo o que você tem a fazer é aproximar x de 2 o suficiente. Ora, e quanto é este "suficiente"? Pelo que acabamos de ver, se você quiser que a diferença entre (3x + 4)/3 e 10/3 seja menor do que ? basta pôr a diferença entre x e 2 também menor do que ? (ou mesmo igual a?).
Exemplo: se você quer que a diferença seja menor do que 0,0000000001 basta pôr ? = 0,0000000001 (ou igual a qualquer número positivo menor do que este).
Referências: os mesmos livros de cálculo listados na referência desta outra postagem.
Erros podem ser relatados aqui.
- Provando Um Limite [dúvida De Um Leitor]
A pedido de um leitor, nesta postagem apresento solução para um problema envolvendo a noção de limite. O enunciado pede para provar a seguinte igualdade: $$ \lim_{x \rightarrow 1} \frac{x^2}{3x - 4} = -1$$ De acordo com a definição...
- O Algoritmo Da Divisão Parte Iii
Nesta série de postagens estamos demonstrando o algoritmo da divisão: Se aé um número inteiro qualquer e bé um número inteiro maior do que zero, então existem dois números inteiros qe rtais que a= bq+ r, onde 0 ? r < b. Além disso, qe rsão...
- Demonstrações De Teoremas Sobre Limites [2]
Teorema 4: Se c e b são números reais quaisquer, então O teorema acima é o Teorema 1 no caso em que m = 0. Uma vez que na demonstração do Teorema 1 dividimos por m (por isso exigiu-se m ? 0 no enunciado) aquela demonstração não vale...
- Demonstrações De Teoremas Sobre Limites [parte I]
Geralmente, quando nos deparamos com limites como os exemplos que se seguem, não temos dificuldades em resolvê-los: É comum adotarmos o procedimento da substituição direta, ou seja, apenas trocamos o x na função pelo...
- Sobre A Definição Formal De Limite
O conceito de limite, embora usualmente seja estudado no nível superior, está presente em alguns pontos estudados no nível básico, como por exemplo no caso da dedução da fórmula que fornece a soma dos infinitos termos de uma PG. O conceito...
