Matemática
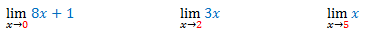
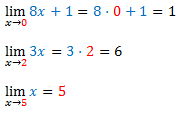
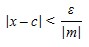
Agora ficou fácil, pois de tal modo reescrevemos as expressões que nos restou apenas mostrar que para qualquer ? positivo sempre existe um ? positivo que torna a seguinte implicação válida:
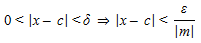
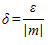
Por exemplo, se ? = 0,00001 e m = 8 basta colocar ? = 0,00000125. Deste modo, exibimos o ?, provando que ele existe e, portanto, o teorema está demonstrado.
- Provando Um Limite [dúvida De Um Leitor]
A pedido de um leitor, nesta postagem apresento solução para um problema envolvendo a noção de limite. O enunciado pede para provar a seguinte igualdade: $$ \lim_{x \rightarrow 1} \frac{x^2}{3x - 4} = -1$$ De acordo com a definição...
- O Algoritmo Da Divisão Parte Iv [o Fim]
Esta é a última postagem da série que teve o objetivo de demonstrar o algoritmo da divisão: Se a é um número inteiro qualquer e b é um número inteiro maior do que zero, então existem dois números inteiros q e r tais...
- O Algoritmo Da Divisão Parte Iii
Nesta série de postagens estamos demonstrando o algoritmo da divisão: Se aé um número inteiro qualquer e bé um número inteiro maior do que zero, então existem dois números inteiros qe rtais que a= bq+ r, onde 0 ? r < b. Além disso, qe rsão...
- Demonstrações De Teoremas Sobre Limites [2]
Teorema 4: Se c e b são números reais quaisquer, então O teorema acima é o Teorema 1 no caso em que m = 0. Uma vez que na demonstração do Teorema 1 dividimos por m (por isso exigiu-se m ? 0 no enunciado) aquela demonstração não vale...
- Sobre Demonstrações Envolvendo Limites E A Definição ?-?
Recapitulando a definição formal: Dizer que o limite de f(x), para x tendendo a c, é L significa que para qualquer que seja ? > 0 existe um ? > 0 tal que, para todo x diferente de c, se 0 < | x ? c | < ? então |f(x) ? L| < ?....
Matemática
Demonstrações de teoremas sobre limites [parte I]
Geralmente, quando nos deparamos com limites como os exemplos que se seguem, não temos dificuldades em resolvê-los:
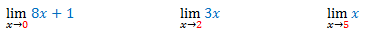
É comum adotarmos o procedimento da substituição direta, ou seja, apenas trocamos o x na função pelo número a que ele tende e calculamos o valor da expressão:
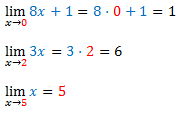
Quando calculamos limites semelhantes a estes estamos, na verdade, fazendo uso do seguinte teorema:
Teorema 1: Se b e c são números reais quaisquer e m é um número real diferente de zero, então 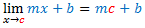 |
Para demonstrar este teorema vamos, primeiramente, enunciá-lo novamente nos moldes da definição formal: Se b e c são números reais quaisquer e m é um número real diferente de zero, então para todo ? > 0 existe um ? > 0 tal que
0 < |x ? c| < ? ? |(mx + b) ? (mc + b)| < ?
Mas como o vamos provar? Ora, mostraremos que de fato existe um ? para qualquer que for o ? dado.
E como mostraremos que ?existe um ??? Vamos exibí-lo, como se segue ? começando por reescrever o lado direito da implicação por meio de algumas manipulações algébricas:
|(mx + b) ? (mc + b)| = |mx + b ? mc ? b|
= |mx ? mc + b ? b|
= |(mx ? mc) + (b ? b)|
= |m(x ? c) + 0|
= |m(x ? c)|
= |m||x ? c|
Portanto (substituindo este último resultado na primeira implicação) o que temos que fazer é mostrar que para todo ? > 0 existe um ? > 0 tal que
0 < |x ? c| < ? ? |m||x ? c| < ?
Como m é diferente de zero (pois o enunciado do teorema diz isso) podemos reescrever a desigualdade |m||x ? c| < ? do seguinte modo:
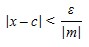
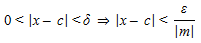
Note que para qualquer que for o ? dado existe uma particular escolha para ? que torna a implicação acima válida. De fato, basta escolher:
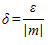
Observe que o que aconteceu nesta demonstração, e acontecerá nas demonstrações seguintes, é que expressamos o ? em função do ?. Assim, uma vez que o ? for dado o ? também fica dado.
Observe ainda que o que acabamos de fazer foi mostrar que podemos tornar o valor de mx + b tão próximo de mc + b quanto quisermos. Basta para isso tomar x suficientemente próximo de c (mas nunca igual a c). Transferindo isso para o caso do primeiro exemplo dado no início da postagem: podemos tornar o valor de 8x + 1 tão próximo de 1 quanto quisermos. Basta para isso tomar x suficientemente próximo de 0 (mas nunca igual a 0).
Segue imediatamente do Teorema 1 o seguinte resultado:
Teorema 2: Se c é um número real qualquer e m é um número real diferente de zero, então 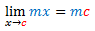 |
O teorema acima é, evidentemente, o Teorema 1 para o caso em que b = 0 e, portanto, já está demonstrado. Contudo sua demonstração pode ser feita diretamente pela definição de modo análogo ao que foi feito acima ? fica a sugestão para o leitor fazê-la. A aplicação do Teorema 2 está ilustrada no segundo exemplo dado no início da postagem.
Agora, pondo m = 1 no Teorema 2 obtemos:
Agora, pondo m = 1 no Teorema 2 obtemos:
Teorema 3: Se c é um número real qualquer, então 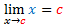 |
O Teorema 3 por sua vez, está ilustrado no último exemplo dado no início da postagem e também pode ser demonstrado diretamente por meio da definição de limite, tal qual fizemos no primeiro teorema.
Nesta postagem abordamos o Teorema 1 para o caso em que m = 0.
Referências: Livros de Cálculo.
Erros podem ser apontados aqui.
Erros podem ser apontados aqui.
- Provando Um Limite [dúvida De Um Leitor]
A pedido de um leitor, nesta postagem apresento solução para um problema envolvendo a noção de limite. O enunciado pede para provar a seguinte igualdade: $$ \lim_{x \rightarrow 1} \frac{x^2}{3x - 4} = -1$$ De acordo com a definição...
- O Algoritmo Da Divisão Parte Iv [o Fim]
Esta é a última postagem da série que teve o objetivo de demonstrar o algoritmo da divisão: Se a é um número inteiro qualquer e b é um número inteiro maior do que zero, então existem dois números inteiros q e r tais...
- O Algoritmo Da Divisão Parte Iii
Nesta série de postagens estamos demonstrando o algoritmo da divisão: Se aé um número inteiro qualquer e bé um número inteiro maior do que zero, então existem dois números inteiros qe rtais que a= bq+ r, onde 0 ? r < b. Além disso, qe rsão...
- Demonstrações De Teoremas Sobre Limites [2]
Teorema 4: Se c e b são números reais quaisquer, então O teorema acima é o Teorema 1 no caso em que m = 0. Uma vez que na demonstração do Teorema 1 dividimos por m (por isso exigiu-se m ? 0 no enunciado) aquela demonstração não vale...
- Sobre Demonstrações Envolvendo Limites E A Definição ?-?
Recapitulando a definição formal: Dizer que o limite de f(x), para x tendendo a c, é L significa que para qualquer que seja ? > 0 existe um ? > 0 tal que, para todo x diferente de c, se 0 < | x ? c | < ? então |f(x) ? L| < ?....
