Matemática
Recapitulando a definição formal: Dizer que o limite de f(x), para x tendendo a c, é L significa que para qualquer que seja ? > 0 existe um ? > 0 tal que, para todo x diferente de c, se 0 < | x ? c | < ? então |f(x) ? L| < ?. Utiliza-se a seguinte notação:
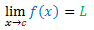
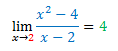
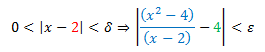
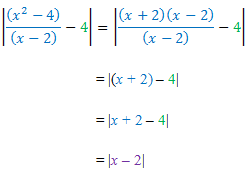
Se dissermos, portanto, que ?cumprir a condição P? significa satisfazer a desigualdade 0 < | x ? c | < ? e que ?cumprir a condição Q? significa satisfazer a desigualdade |f(x) ? L| < ?, a demonstração se resume a encontrar um ? conveniente que torne o conjunto A um subconjunto do conjunto B, para qualquer que for o ? dado.
Referências: Guidorizzi; Leithold; Stewart; Larson.
- Provando Um Limite [dúvida De Um Leitor]
A pedido de um leitor, nesta postagem apresento solução para um problema envolvendo a noção de limite. O enunciado pede para provar a seguinte igualdade: $$ \lim_{x \rightarrow 1} \frac{x^2}{3x - 4} = -1$$ De acordo com a definição...
- O Algoritmo Da Divisão Parte Iii
Nesta série de postagens estamos demonstrando o algoritmo da divisão: Se aé um número inteiro qualquer e bé um número inteiro maior do que zero, então existem dois números inteiros qe rtais que a= bq+ r, onde 0 ? r < b. Além disso, qe rsão...
- Demonstrações De Teoremas Sobre Limites [2]
Teorema 4: Se c e b são números reais quaisquer, então O teorema acima é o Teorema 1 no caso em que m = 0. Uma vez que na demonstração do Teorema 1 dividimos por m (por isso exigiu-se m ? 0 no enunciado) aquela demonstração não vale...
- Demonstrações De Teoremas Sobre Limites [parte I]
Geralmente, quando nos deparamos com limites como os exemplos que se seguem, não temos dificuldades em resolvê-los: É comum adotarmos o procedimento da substituição direta, ou seja, apenas trocamos o x na função pelo...
- Sobre A Definição Formal De Limite
O conceito de limite, embora usualmente seja estudado no nível superior, está presente em alguns pontos estudados no nível básico, como por exemplo no caso da dedução da fórmula que fornece a soma dos infinitos termos de uma PG. O conceito...
Matemática
Sobre demonstrações envolvendo limites e a definição ?-?
Recapitulando a definição formal: Dizer que o limite de f(x), para x tendendo a c, é L significa que para qualquer que seja ? > 0 existe um ? > 0 tal que, para todo x diferente de c, se 0 < | x ? c | < ? então |f(x) ? L| < ?. Utiliza-se a seguinte notação:
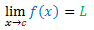
Conforme foi visto na última postagem isso é um modo formal de dizer que quando x se aproxima de c, f(x) se aproxima de L com o valor de f(x) podendo ficar tão próximo de L quanto quisermos, bastando para isso aproximar x de c o suficiente.
Então, para provar que o limite de f(x), para x tendendo a c, é L temos que mostrar que para qualquer ? dado existe um ? que torna a seguinte implicação verdadeira:
0 < | x ? c | < ? ? | f(x) ? L | < ?
Muitas vezes o que temos que fazer é reescrever o lado direito da implicação. No exemplo considerado na última postagem vimos graficamente que:
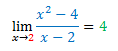
Se a intenção fosse provar isso utilizando a definição formal teríamos que mostrar que para qualquer ? > 0 existe um ? > 0 tal que para todo x diferente de c:
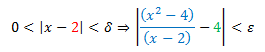
Mas observe o seguinte:
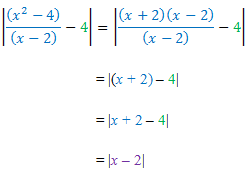
Portanto, tudo se resume em mostrar que para qualquer ? positivo existe um ? positivo tal que a seguinte implicação é válida:
0 < |x ? 2| < ? ? |x ? 2| < ?
Veja, por exemplo, que se ? = 0,01 temos que mostrar que existe um ? tal que
0 < |x ? 2| < ? ? |x ? 2| < 0,01
Este é um dos casos mais simples. Evidentemente existe um ? que torna a implicação acima válida. Basta escolher ? = 0,01. De fato:
0 < |x ? 2| < 0,01 ? |x ? 2| < 0,01
Agora se for dado, por exemplo, ? = 0,0001 tudo o que temos que fazer é escolher ? = 0,0001. Para esta função em particular basta sempre escolher ? = ?, para qualquer que for o ? dado.
Observação:
Antes de considerar qualquer teorema sobre limite, talvez seja conveniente relembrar o significado de uma implicação lógica ? já que as demonstrações se baseiam nelas.
Sejam A e B dois conjuntos definidos como se segue:
A = {x, tal que x cumpre a condição P}
B = {x, tal que x cumpre a condição Q}
Dizer algumas das sentenças abaixo (que são todas equivalentes)
- P implica Q
- Se P então Q
- P é condição suficiente para Q
- P somente se Q
- Q é condição necessária para P
Continua aqui.
Erros podem ser apontados aqui.
_______________________________________________________________
VEJA TAMBÉM
Sobre a definição formal de limite
Demonstrações de teoremas sobre limites
Demonstrações de teoremas sobre limites
_______________________________________________________________
- Provando Um Limite [dúvida De Um Leitor]
A pedido de um leitor, nesta postagem apresento solução para um problema envolvendo a noção de limite. O enunciado pede para provar a seguinte igualdade: $$ \lim_{x \rightarrow 1} \frac{x^2}{3x - 4} = -1$$ De acordo com a definição...
- O Algoritmo Da Divisão Parte Iii
Nesta série de postagens estamos demonstrando o algoritmo da divisão: Se aé um número inteiro qualquer e bé um número inteiro maior do que zero, então existem dois números inteiros qe rtais que a= bq+ r, onde 0 ? r < b. Além disso, qe rsão...
- Demonstrações De Teoremas Sobre Limites [2]
Teorema 4: Se c e b são números reais quaisquer, então O teorema acima é o Teorema 1 no caso em que m = 0. Uma vez que na demonstração do Teorema 1 dividimos por m (por isso exigiu-se m ? 0 no enunciado) aquela demonstração não vale...
- Demonstrações De Teoremas Sobre Limites [parte I]
Geralmente, quando nos deparamos com limites como os exemplos que se seguem, não temos dificuldades em resolvê-los: É comum adotarmos o procedimento da substituição direta, ou seja, apenas trocamos o x na função pelo...
- Sobre A Definição Formal De Limite
O conceito de limite, embora usualmente seja estudado no nível superior, está presente em alguns pontos estudados no nível básico, como por exemplo no caso da dedução da fórmula que fornece a soma dos infinitos termos de uma PG. O conceito...
