Matemática
Parabéns Marcos Valle, por resolver um de nossos desafios

Abaixo segue a resolução:
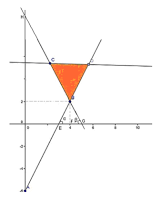
Seja y = mx + h a equação da reta buscada.
$$\bigtriangleup{AOE} \sim \bigtriangleup{EFB}$$
Razão de semelhança linear: $$k = \frac{6}{2} = 3$$
Logo:
m(OE) = 3 e m(EF) = 1
Calculemos o coeficiente angular da reta BC:
$$Tg\alpha = \frac{m(BF)}{m(EF)} = 2$$
$$Tg\beta = Tg\left(\frac{2\pi}{3} - \alpha\right)$$
$$Tg\beta = \frac{Tg(2\pi/3) - Tg\alpha}{1 + Tg(2\pi/3).Tg\alpha}$$
$$Tg\beta = -\frac{\sqrt{3} + 2}{1 - 2\sqrt{3}}$$
Portanto, $$m = Tg(\pi - \beta) = \frac{\sqrt{3} + 2}{1 - 2\sqrt{3}}$$
Para encontrar o coeficiente linear, façamos:
$$Tg\beta = \frac{m(BF)}{m(FG)}$$
$$m(FG) = \frac{2 - 4\sqrt{3}}{sqrt{3} + 2}$$
Mas:
$$\bigtriangleup{HOG} \sim \bigtriangleup{BFG}$$
$$\frac{m(OH)}{m(FB)} = \frac{m(OG)}{m(FG)}$$
$$h = m(OH) = \frac{2.(4 - 2 - 4\sqrt{3}/\sqrt{3} + 2)}{-2-4\sqrt{3}/\sqrt{3} + 2}$$
$$h = 2 - \frac{4(\sqrt{3} + 2)}{1 - 2\sqrt{3}}$$
Assim:
$$y = \left(\frac{\sqrt{3} + 2}{1 - 2\sqrt{3}}\right)x + \left(2 - \frac{4(\sqrt{3} + 2)}{1 - 2\sqrt{3}}\right)$$
Racionalizando chegamos a:
$$(8 + 5\sqrt{3})x + 11y - (54 + 20\sqrt{3} ) = 0$$
O Marcos Valle também resolveu através de geometria analítica. Quem quiser as resoluções em .pdf entre em contato conosco pelo e-mail: [email protected]
Em breve outro desafio.
- Equação Do Segundo Grau - Parte Ii - Fórmula De Bhaskara E Outros
Olá, gente. Há um tempo eu postei algo sobre equações do segundo grau (clique aqui para ver).Analisaremos o caso em que temos , onde x é a incógnita, e . Para este caso, há 3 formas principais de resolver tal equação, são elas: I- Completar...
- Desafio - Física
Na figura, um bloco sobe um plano inclinado, com velocidade inicial $$V_0$$. Considere $$\mu$$ o coeficiente de atrito entre o bloco e a superfície. Indique sua velocidade ao passar pela posição inicial. A. $$V_0\sqrt{\frac{sen\theta - \mu cos\theta}{sen\theta...
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a}\ Dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a}\ dx = \frac{\displaystyle \text{arctg}\left( \frac{x}{\sqrt{a}}\right)}{\sqrt{a}}+C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2+a \neq...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Retificação Da Circunferência (parte 7)
Hoje, 14 de março, (do inglês 3/14), comemora-se o dia internacional do $\pi$. Como forma de homenagear esta constante, que desde os egípcios antigos persegue os matemáticos, desenvolvi esta construção com apenas régua e compasso, onde podemos...
Matemática
Desafio Resolvido
Parabéns Marcos Valle, por resolver um de nossos desafios
Abaixo segue a resolução:

clique na imagem para ver maior
Seja y = mx + h a equação da reta buscada.
$$\bigtriangleup{AOE} \sim \bigtriangleup{EFB}$$
Razão de semelhança linear: $$k = \frac{6}{2} = 3$$
Logo:
m(OE) = 3 e m(EF) = 1
Calculemos o coeficiente angular da reta BC:
$$Tg\alpha = \frac{m(BF)}{m(EF)} = 2$$
$$Tg\beta = Tg\left(\frac{2\pi}{3} - \alpha\right)$$
$$Tg\beta = \frac{Tg(2\pi/3) - Tg\alpha}{1 + Tg(2\pi/3).Tg\alpha}$$
$$Tg\beta = -\frac{\sqrt{3} + 2}{1 - 2\sqrt{3}}$$
Portanto, $$m = Tg(\pi - \beta) = \frac{\sqrt{3} + 2}{1 - 2\sqrt{3}}$$
Para encontrar o coeficiente linear, façamos:
$$Tg\beta = \frac{m(BF)}{m(FG)}$$
$$m(FG) = \frac{2 - 4\sqrt{3}}{sqrt{3} + 2}$$
Mas:
$$\bigtriangleup{HOG} \sim \bigtriangleup{BFG}$$
$$\frac{m(OH)}{m(FB)} = \frac{m(OG)}{m(FG)}$$
$$h = m(OH) = \frac{2.(4 - 2 - 4\sqrt{3}/\sqrt{3} + 2)}{-2-4\sqrt{3}/\sqrt{3} + 2}$$
$$h = 2 - \frac{4(\sqrt{3} + 2)}{1 - 2\sqrt{3}}$$
Assim:
$$y = \left(\frac{\sqrt{3} + 2}{1 - 2\sqrt{3}}\right)x + \left(2 - \frac{4(\sqrt{3} + 2)}{1 - 2\sqrt{3}}\right)$$
Racionalizando chegamos a:
$$(8 + 5\sqrt{3})x + 11y - (54 + 20\sqrt{3} ) = 0$$
O Marcos Valle também resolveu através de geometria analítica. Quem quiser as resoluções em .pdf entre em contato conosco pelo e-mail: [email protected]
Em breve outro desafio.
- Equação Do Segundo Grau - Parte Ii - Fórmula De Bhaskara E Outros
Olá, gente. Há um tempo eu postei algo sobre equações do segundo grau (clique aqui para ver).Analisaremos o caso em que temos , onde x é a incógnita, e . Para este caso, há 3 formas principais de resolver tal equação, são elas: I- Completar...
- Desafio - Física
Na figura, um bloco sobe um plano inclinado, com velocidade inicial $$V_0$$. Considere $$\mu$$ o coeficiente de atrito entre o bloco e a superfície. Indique sua velocidade ao passar pela posição inicial. A. $$V_0\sqrt{\frac{sen\theta - \mu cos\theta}{sen\theta...
- Resolução Da Integral $\displaystyle \int \frac{1}{x^2+a}\ Dx$
Nesta postagem, vamos provar que: \begin{equation*} \int \frac{1}{x^2+a}\ dx = \frac{\displaystyle \text{arctg}\left( \frac{x}{\sqrt{a}}\right)}{\sqrt{a}}+C \end{equation*} onde $a$ é uma constante, tal que $a \in \mathbb{R}^\ast$, sendo $x^2+a \neq...
- Resolução Da Integral $\int \frac{x^2}{(4-x^2)^{3/2}}dx$
Li em um livro, talvez no do Simmons ou do Foulis, que integrar é uma arte. E é verdade. Quanto mais resolvo, mais percebo que não basta apenas o trivial. Esta integral foi enviada por um leitor por e-mail. Só consegui resolvê-la com uma ajuda da...
- Retificação Da Circunferência (parte 7)
Hoje, 14 de março, (do inglês 3/14), comemora-se o dia internacional do $\pi$. Como forma de homenagear esta constante, que desde os egípcios antigos persegue os matemáticos, desenvolvi esta construção com apenas régua e compasso, onde podemos...
