Matemática

Retificação da Circunferência (Parte 7)

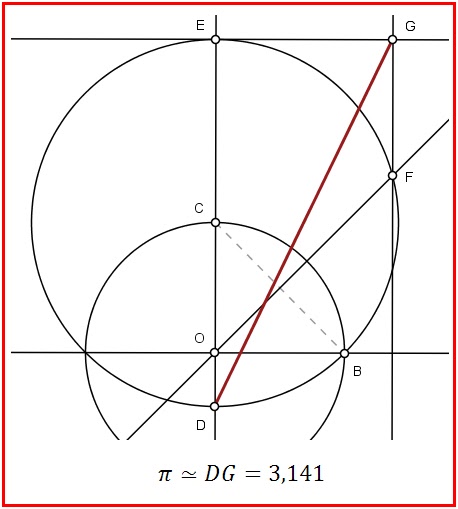
Hoje, 14 de março, (do inglês 3/14), comemora-se o dia internacional do $\pi$. Como forma de homenagear esta constante, que desde os egípcios antigos persegue os matemáticos, desenvolvi esta construção com apenas régua e compasso, onde podemos aproximar $\pi$ em três casas decimais por um seguimento de reta.

Construção:

1) Trace um par de eixos ortogonais e descreva uma circunferência de raio unitário centrada na origem $O$ marcando os pontos $B$ e $C$ na intersecção com a circunferência.

2) Com centro em $C$ e raio $CB=\sqrt{2}$, descreva uma circunferência e marque os pontos $D$ e $E$ no eixo vertical.

3) Trace a bissetriz do ângulo $\angle BAC$ e marque o ponto $F$ na intersecção com a circunferência de centro $C$.

4) Trace um seguimento vertical por $F$ e um segmento horizontal por $E$. A intersecção desses segmentos gera o ponto $G$.

5) O segmento $DG$ aproxima $\pi$ em $\pi=3,141$.

Demonstração:

Seja $\alpha:x^2+y^2=1$ a circunferência de raio unitário centrada na origem. Seja $\beta$ a circunferência de raio $\sqrt{2}$ centrada no ponto $C(0,1)$, ou seja:

$$\beta:x^2+(y-1)^2=2$$

Vejam que $\beta$ intercepta o eixo dos $y$ nos pontos $y=1\pm \sqrt{2}$. Assim, $D(0,1-\sqrt{2})$ e $E(1+\sqrt{2})$.

Por construção, $BC$ é a bissetriz dos quadrantes ímpares e, portanto, o ponto $F$ é resultante da intersecção de $r$ com $\beta$ e é dado pelo sistema de equações:

$$
\left\{\begin{matrix}
x^2+(y-1)^2&=&2\\
y&=&x
\end{matrix}\right.
$$
ou seja:
\begin{matrix}
x^2+(x+1)^2=2\\
2x^2-2x-1=0\\
x_F=\frac{1+\sqrt{3}}{2}\\
\end{matrix}
Assim, as coordenadas do ponto $G$ são $x_F$ e $y_E$, ou seja:
$$G\left (\frac{1+\sqrt{3}}{2},1+\sqrt{2}\right )$$
Logo,
\begin{matrix}
DG^2=\left (\frac{1+\sqrt{3}}{2}-0 \right)^2 + \left (1+\sqrt{2}-1+\sqrt{2}\right)^2\\
DG^2=\frac{(1+\sqrt{3})^2}{4}+(2\sqrt{2})^2\\
DG^2=9+\frac{\sqrt{3}}{2}\\
DG=\sqrt{\frac{18+\sqrt{3}}{2}}\\
DG\simeq 3,141\\
\end{matrix}

Uma curiosidade nesta construção é que temos a presença de uma outra constante irracional, o número prateado, representado por $\delta_S=1+\sqrt{2}$.

Veja mais:

Retificação da Circunferência (Parte 6) - Método de Specht
Newton e a Série Infinita para $\pi$
Aproximação de $\pi$ Como Soma de Dois Números Irracionais
O Número Prateado

- Desafio Resolvido
Parabéns Marcos Valle, por resolver um de nossos desafios Abaixo segue a resolução: clique na imagem para ver maior Seja y = mx + h a equação da reta buscada. $$\bigtriangleup{AOE} \sim \bigtriangleup{EFB}$$ Razão de semelhança linear: $$k = \frac{6}{2}...

- Resolução Da Integral $\displaystyle \int$ $\frac{1}{ax^2+bx+c}\ Dx$
Nesta postagem, vamos demonstrar que: \begin{equation*} \int \frac{1}{ax^2+bx+c}\ dx = 2\ \text{arctg}\left( \frac{2ax+b}{\displaystyle \sqrt{a}\sqrt{4c-\frac{b^2}{a}}} \right) + C \end{equation*} onde $a$, $b$ e $c$ são constantes, onde $a$, $b$ e $c$ ...

- Construção De Um Pentágono Regular Com Régua E Compasso (parte 4) - Método De Hirano
Esta é uma elegante construção do pentágono regular pelos métodos euclidianos, elaborado por Yoshifusa Hirano. A construção foi incluída num manuscrito Sanpo Jyojutu Kaigi, por Chorin Kawakita $(1840-1919)$ que escreveu:"Hirano descobriu...

- Os $10$ Problemas De Apolônio: Problema $1:[ppp]$ Problema Dos Três Pontos
Este é o mais simples dos problemas sobre tangências de Apolônio, que se resume em descrever uma circunferência que passa por três pontos dados não-colineares. Sejam três pontos não-colineares quaisquer $A$, $B$ e $C$ no plano. Para descrevermos...

- A Equação Da Elipse
Consideremos num plano, dois pontos $F_1$ e $F_2$ distantes um do outro por $2c>0$ e seja $a>c$. Definição $1$:Elipse é o lugar geométrico dos pontos de um plano onde a soma das distâncias a dois pontos fixos desse plano é constante. Dá-se...

Matemática