Matemática

Divisão de um Segmento de Reta em n Partes Iguais

Às vezes precisamos relembrar certos conceitos, pois ficam esquecidos em nossa mente. Algo simples como dividir um segmento de reta em partes n iguais faltou a minha memória. Fui buscar então a resposta e aproveito para expor aqui a resolução.

Este problema consiste em dividir um segmento de reta em n partes iguais, mas sem utilizar a graduação de uma régua. Como fazer então?

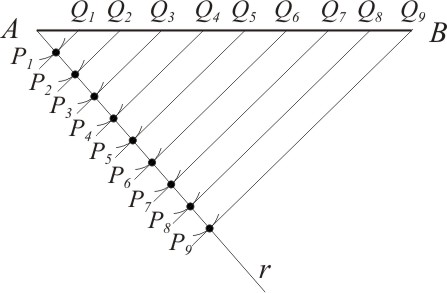
Iniciemos com o segmento de reta AB onde pretendemos dividi-lo em n partes iguais. Como forma de exemplo, vamos dividi-lo em 9 partes iguais. Para isso, tracemos a reta r passando pelo ponto A, com comprimento indefinido. Pode ser aproximadamente o mesmo tamanho do segmento AB, não precisamos exagerar. Já o ângulo, melhor que seja agudo, pois ficam mais fáceis os traçados. Feito isso, utilizando um compasso, vamos descrever arcos de circunferências com raio qualquer.

Posicione a ponta seca do compasso sobre o ponto A e descreva um arco interceptando a reta r, marcando o ponto P₁; Com a ponta seca do compasso em P₁ e com mesmo raio, descreva um novo arco sobre a reta r, marcando o ponto P₂; Repita este processo o número de vezes em que se deseje dividir o segmento AB, em nosso caso 9 partes.

Feito isso, trace uma reta transversal passando pelo ponto B e P₉. Agora, trace retas paralelas a este segmento de tal modo que passem pelos pontos P_1,P_{2, ... ,}P_n. As intersecções dessas retas com o segmento AB, geram os pontos Q_n dividindo-o em 9 partes iguais.

Veja quem este processo é simples e muito eficaz e não precisamos ficar medindo os espaços. Funciona sempre. Um velho conceito que não sai de moda.

Veja mais:

Construções Geométricas Utilizando Régua e Compasso

- Como Desenhar Um Ovo De Galinha Com Régua E Compasso (parte 1)
Este é o primeiro post de uma série que pretendo publicar aqui no blog sobre a construção geométrica do ovo de galinha. Não são aproximações, são curvas reais dos ovos. Robert Dixon, em seu livro Mathographics, de 1987, denomina essas curvas...

- Retificação Da Circunferência (parte 4)
Ficou provado que é impossível a construção de um quadrado com mesma área que um círculo utilizando instrumentos euclidianos. O que conseguimos são somente boas aproximações. Encontrar um segmento de reta que aproxime $\pi$ também mobiliza muitos...

- Construção Geométrica Da Espiral De Arquimedes Com Régua E Compasso
Os trabalhos de Arquimedes são obras-primas de exposição matemática. Além de exibirem grande originalidade, habilidade computacional e rigor nas demonstrações, são escritos numa linguagem altamente acabada e objetiva. Cerca de dez tratados de...

- Construção Geométrica Da Parábola Com Régua E Compasso
Considere em um plano uma reta $d$ e um ponto $F$ não pertencente à $d$. A parábola é o lugar geométrico dos pontos do plano que estão equidistantes a $d$ e a $F$. Temos que: $\bullet$ O ponto $F$ é o foco da parábola; $\bullet$ A reta $d$ é...

- Retificação Da Circunferência (parte 1)
Neste post faremos a retificação da circunferência. O segmento encontrado nos remeterá a um valor aproximado de π. Dada uma circunferência de raio R, como determinar o valor de seu comprimento? Podemos utilizar a conhecida fórmula: C = 2πR. Vamos...

Matemática