Matemática
Função é a relação do conjunto de chegada com o conjunto de partida, a forma que assumir essa relação poderá definir uma função como sendo par ou ímpar.
Função par
Será uma função par a relação onde o elemento simétrico do conjunto do domínio tiver a mesma imagem no conjunto de chegada. Ou seja, uma função será par se f(x) = f(-x).
Por exemplo: a função A→B, com A = {-2,-1,0,1,2} e B = {1,2,5} definida pela fórmula f(x) = x2 + 1, obedece o seguinte diagrama:
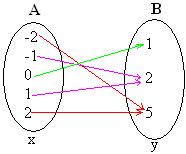
Veja nesse diagrama que os elementos simétricos do domínio, como o 2 e -2, possuem a mesma imagem. Por isso, essa função é uma função par.
Outra forma de verificar se uma função é par é a seguinte: para que uma função seja par é preciso que f(x) = f(-x), então, se for dada a seguinte função f(x) = x2 + 1, basta substituir.
Como f(x) = f(-x), então f(-x) = (-x)2 – 1 → f (-x) = x2 – 1. A função continuou a mesma depois da substituição, portanto, ela é uma função par.
Função ímpar
Será uma função ímpar a relação onde os elementos simétricos do conjunto do domínio terão imagens simétricas no conjunto de chegada. Ou seja, uma função será ímpar se
f(-x) = -f(x).
Por exemplo: a função A→B, com A = {-2,-1,0,1,2} e B = {-10,-5,0,5,10} definida pela fórmula f(x) = 5x, obedece o seguinte diagrama:
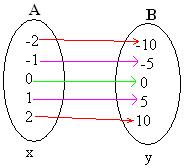
Veja que os elementos simétricos do conjunto A como -2 e 2 possuem imagens simétricas. Por isso, essa função é uma função ímpar.
Outra forma de verificar se uma função é ímpar é a seguinte: para que uma função seja ímpar é preciso que f(-x) = -f(x), então se for dada a seguinte função f(x) = 5x, basta testar se ela seria par.
Como f(x) = f(-x), então f(-x) = 5 . (-x) → f (-x) = -5x. Como a função f(x) ≠ f(-x) e
f(-x) = -f(x), dizemos que essa função é uma função ímpar.
mundoeducacao
- Função Inversa
O objetivo de uma função inversa é criar funções a partir de outras. Uma função somente será inversa se for bijetora, isto é, os pares ordenados da função f deverão pertencer à função inversa f –1 da seguinte maneira: (x,y) Є f –1...
- Relação E Função
Se em uma relação de dois conjuntos A e B, todos os elementos x de A estiver relacionados com um elemento y de B, dizemos que essa relação é uma função bijetora. Toda função bijetora tem a sua forma inversa. Veja um exemplo de função bijetora...
- Função Inversa
O objetivo de uma função inversa é criar funções a partir de outras. Uma função somente será inversa se for bijetora, isto é, os pares ordenados da função f deverão pertencer à função inversa f –1 da seguinte maneira: (x,y) Є f –1...
- Propriedades De Uma Função
As funções, independentes do grau que ela seja, são caracterizadas conforme a ligação entre os elementos dos conjuntos onde é feita a relação. Uma função A →B pode ser: sobrejetora, injetora, e bijetora. Para identificarmos essas características...
- Propriedades De Uma Função
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com ...
Matemática
Função par e função ímpar
Função é a relação do conjunto de chegada com o conjunto de partida, a forma que assumir essa relação poderá definir uma função como sendo par ou ímpar.
Função par
Será uma função par a relação onde o elemento simétrico do conjunto do domínio tiver a mesma imagem no conjunto de chegada. Ou seja, uma função será par se f(x) = f(-x).
Por exemplo: a função A→B, com A = {-2,-1,0,1,2} e B = {1,2,5} definida pela fórmula f(x) = x2 + 1, obedece o seguinte diagrama:
Veja nesse diagrama que os elementos simétricos do domínio, como o 2 e -2, possuem a mesma imagem. Por isso, essa função é uma função par.
Outra forma de verificar se uma função é par é a seguinte: para que uma função seja par é preciso que f(x) = f(-x), então, se for dada a seguinte função f(x) = x2 + 1, basta substituir.
Como f(x) = f(-x), então f(-x) = (-x)2 – 1 → f (-x) = x2 – 1. A função continuou a mesma depois da substituição, portanto, ela é uma função par.
Função ímpar
Será uma função ímpar a relação onde os elementos simétricos do conjunto do domínio terão imagens simétricas no conjunto de chegada. Ou seja, uma função será ímpar se
f(-x) = -f(x).
Por exemplo: a função A→B, com A = {-2,-1,0,1,2} e B = {-10,-5,0,5,10} definida pela fórmula f(x) = 5x, obedece o seguinte diagrama:
Veja que os elementos simétricos do conjunto A como -2 e 2 possuem imagens simétricas. Por isso, essa função é uma função ímpar.
Outra forma de verificar se uma função é ímpar é a seguinte: para que uma função seja ímpar é preciso que f(-x) = -f(x), então se for dada a seguinte função f(x) = 5x, basta testar se ela seria par.
Como f(x) = f(-x), então f(-x) = 5 . (-x) → f (-x) = -5x. Como a função f(x) ≠ f(-x) e
f(-x) = -f(x), dizemos que essa função é uma função ímpar.
mundoeducacao
- Função Inversa
O objetivo de uma função inversa é criar funções a partir de outras. Uma função somente será inversa se for bijetora, isto é, os pares ordenados da função f deverão pertencer à função inversa f –1 da seguinte maneira: (x,y) Є f –1...
- Relação E Função
Se em uma relação de dois conjuntos A e B, todos os elementos x de A estiver relacionados com um elemento y de B, dizemos que essa relação é uma função bijetora. Toda função bijetora tem a sua forma inversa. Veja um exemplo de função bijetora...
- Função Inversa
O objetivo de uma função inversa é criar funções a partir de outras. Uma função somente será inversa se for bijetora, isto é, os pares ordenados da função f deverão pertencer à função inversa f –1 da seguinte maneira: (x,y) Є f –1...
- Propriedades De Uma Função
As funções, independentes do grau que ela seja, são caracterizadas conforme a ligação entre os elementos dos conjuntos onde é feita a relação. Uma função A →B pode ser: sobrejetora, injetora, e bijetora. Para identificarmos essas características...
- Propriedades De Uma Função
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br www.accbarrosogestar.wordpress.com ...
