Matemática
Na equação de primeiro grau 2x - 6 = 0, temos que x = 3, ou seja, a raiz da equação vale 3 ou, ainda, o valor de x que torna verdadeira a sentença é 3, pois 2.3 - 6 = 0.
Agora, vamos pensar na inequação, isto é, na desigualdade:
Na inequaçãode primeiro grau 2x - 6 > 0, x = 3 não faz parte dos valores de x que tornam verdadeira a sentença, pois 2.3 -6 = 0 e não maior do que zero, como a inequação propõe.
Os valores de x que satisfazem a desigualdade são x > 3. Por exemplo, x = 3,1 já satisfaz. Além disso, x = 4 ou x = 10 também. Assim, qualquer número maior do que 3 satisfaz a desigualdade.
Por isso, escrevemos a solução da inequaçãoassim:
(qualquer x maior do que três no conjunto dos reais; lemos: x pertence aos reais, tal que x é maior do que três), no caso do conjunto universo ser o dos reais.
Agora vamos à resolução de inequações.
No caso da inequaçãode primeiro grau, "isola-se" o x como na equação de primeiro grau, observando as propriedades da desigualdade.
Exemplos:
Assim, nesse último caso, ao multiplicarmos os dois membros da desigualdade por -1, o sinal da desigualdade é invertido, para que a sentença continue verdadeira. Basta observarmos o exemplo 2 < 3. Se multiplicarmos os dois membros por -1, a desigualdade deixa de ser verdadeira (-2 < -3 é falso!), obrigando-nos a inverter o sinal da desigualdade (-2 > -3).
Mas existem outros tipos de inequações.
Vejamos dois exemplos:
No exemplo 1, a primeira idéia que podemos ter para resolver é a de aplicarmos a propriedade distributiva, assim:
Porém, como resolver a inequaçãodo segundo grau que surgiu?
Será que devemos pensar no caso da inequaçãode primeiro grau, que é resolvida praticamente da mesma forma que equação de primeiro grau (isolando o x), e tentarmos resolver a inequaçãode segundo grau como a equação, aplicando a fórmula de Bhaskara?
Nesse caso, obteríamos os seguintes valores de x:
Mas, e agora? Como achar a resposta da inequaçãoa partir dos valores encontrados para x? Como a inequaçãoé (x + 5).(- 2x + 4) > 0, poderíamos pensar em x > 2 e x > -5, mas isso não teria muito significado.
Assim, a forma mais correta de resolver as inequaçõespropostas, denominadas, respectivamente, de inequaçãoproduto e inequaçãoquociente, seria pensar da seguinte forma:
no exemplo 1, temos o produto de duas expressões e queremos saber para quais valores de x esse produto é estritamente positivo;
no exemplo 2, temos o quociente de duas expressões e desejamos saber para quais valores de x esse quociente é negativo ou igual a zero.
Assim, seria interessante conhecer os sinais dessas expressões, em ambos os casos, pois conhecemos as regras de sinais da multiplicação e da divisão. Conhecendo os sinais dessas expressões, podemos decidir quando o produto ou quociente serão positivos ou negativos.
Devemos então estudar o sinal das expressões, como se faz com as funções.
Voltemos aos exemplos:
Depois de estudarmos os sinais das duas expressões, devemos analisar o sinal do produto das duas, pois é o que queremos. Assim, devemos colocar as duas funções no mesmo sistema de eixos. Uma forma mais prática e bastante utilizada de se fazer isso é utilizar o quadro de sinais ou "varal".
Assim, podemos fazer as regras de sinais, de acordo com o sinal de cada função, antes de -5, entre -5 e 2 e depois de 2.
Como nos interessa saber quando esse produto é positivo, destacamos o intervalo entre -5 e 2 - utilizando as notações adequadas de intervalos reais - pois foi onde isso aconteceu.
Logo, a solução dessa inequação é
É importante destacar que -5 e 2 não fazem parte da solução, pois são valores onde as funções são nulas, e queremos os valores de x que tornam positivo o produto, não nulo. Isso fica representado no quadro de sinais pelo "buraco" na reta, nesses dois valores. E, na solução, isso fica representado pelo sinal de <, e não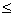 .
.
Essa inequação poderia também ser resolvida se aplicássemos a propriedade distributiva, mas também por meio do estudo do sinal, nesse caso do estudo do sinal da função de segundo grau.
Percebemos que o estudo do sinal revela a mesma solução, ou seja, a função do segundo grau tem as mesmas raízes e os mesmos sinais que o produto das duas funções de primeiro grau estudadas anteriormente. Assim, interessa-nos o intervalo da reta real entre -5 e 2, onde a função é positiva.
Sem precisar traçar os gráficos, podemos esboçá-los, conhecendo as raízes e o crescimento de cada uma, olhando para o sinal do coeficiente de x.
A) coeficiente de x = -1 < 0
Função decrescente
Raiz = 2
B) coeficiente de x = 2 > 0
Função crescente
Raiz =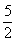
Atenção: Não é o sinal da raiz que determina o crescimento ou decrescimento da função, mas o sinal do coeficiente de x. Esse é um erro bem comum! Cuidado!
Estudados os sinais, vamos ao quadro de sinais:
É importante notar: apesar de querermos os valores de x que tornam o quociente negativo ou nulo, não devemos incluir nunca na solução o valor de x que anula o denomidador da fração (a raiz da expressão do denominador), pois não existe fração com denominador nulo. Esse é outro erro comum!
Logo, a solução é
Michele Viana Debus de França
- Inequação Produto
Algumas inequações apresentam, no 1º membro, produto de funções que para obter a resolução dessas inequações é preciso fazer o estudo do sinal de todas as funções, a solução seria a intersecção do estudo dos sinais das funções que pertencem...
- Inequação Produto
Algumas inequações apresentam, no 1º membro, produto de funções que para obter a resolução dessas inequações é preciso fazer o estudo do sinal de todas as funções, a solução seria a intersecção do estudo dos sinais das funções que pertencem...
- Inequação De 2º Grau
Inequação do 2º grau na variável x é uma expressão matemática de desigualdade escrita nas seguintes formas redutíveis: ax² + bx + c > 0 ax² + bx + c < 0 ax² + bx + c ≥ 0 ax² + bx + c ≤ 0 onde a, b e c pertencem ao conjunto dos números...
- Inequação Produto
Inequação Produto Resolver uma inequação produto consiste em encontrar os valores de x que satisfazem a condição estabelecida pela inequação. Para isso utilizamos o estudo do sinal de uma função. Observe a resolução da seguinte equação produto:...
- Gráfico De Inequações Do 1º Grau
Diferente das equações, as inequações são expressões matemáticas que apresentam em sua configuração sinais de desigualdade. Veja: >: maior que <: menor que ≥: maior ou igual que ≤: menor ou igual que As inequações são utilizadas...
Matemática
Inequação Produto e inequação quociente
Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email [email protected]
www.ensinodematemtica.blogspot.com.br
www.accbarrosogestar.blogspot.com.br
WWW.profantoniocarneiro.com
Na equação de primeiro grau 2x - 6 = 0, temos que x = 3, ou seja, a raiz da equação vale 3 ou, ainda, o valor de x que torna verdadeira a sentença é 3, pois 2.3 - 6 = 0.
Agora, vamos pensar na inequação, isto é, na desigualdade:
Na inequaçãode primeiro grau 2x - 6 > 0, x = 3 não faz parte dos valores de x que tornam verdadeira a sentença, pois 2.3 -6 = 0 e não maior do que zero, como a inequação propõe.
Os valores de x que satisfazem a desigualdade são x > 3. Por exemplo, x = 3,1 já satisfaz. Além disso, x = 4 ou x = 10 também. Assim, qualquer número maior do que 3 satisfaz a desigualdade.
Por isso, escrevemos a solução da inequaçãoassim:
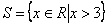 |
(qualquer x maior do que três no conjunto dos reais; lemos: x pertence aos reais, tal que x é maior do que três), no caso do conjunto universo ser o dos reais.
Agora vamos à resolução de inequações.
No caso da inequaçãode primeiro grau, "isola-se" o x como na equação de primeiro grau, observando as propriedades da desigualdade.
Exemplos:
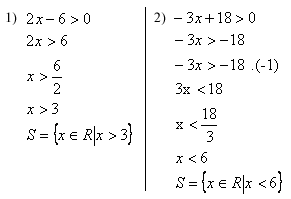 |
Assim, nesse último caso, ao multiplicarmos os dois membros da desigualdade por -1, o sinal da desigualdade é invertido, para que a sentença continue verdadeira. Basta observarmos o exemplo 2 < 3. Se multiplicarmos os dois membros por -1, a desigualdade deixa de ser verdadeira (-2 < -3 é falso!), obrigando-nos a inverter o sinal da desigualdade (-2 > -3).
Mas existem outros tipos de inequações.
Vejamos dois exemplos:
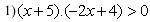 |
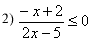 |
No exemplo 1, a primeira idéia que podemos ter para resolver é a de aplicarmos a propriedade distributiva, assim:
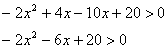 |
Porém, como resolver a inequaçãodo segundo grau que surgiu?
Será que devemos pensar no caso da inequaçãode primeiro grau, que é resolvida praticamente da mesma forma que equação de primeiro grau (isolando o x), e tentarmos resolver a inequaçãode segundo grau como a equação, aplicando a fórmula de Bhaskara?
Nesse caso, obteríamos os seguintes valores de x:
 |
Mas, e agora? Como achar a resposta da inequaçãoa partir dos valores encontrados para x? Como a inequaçãoé (x + 5).(- 2x + 4) > 0, poderíamos pensar em x > 2 e x > -5, mas isso não teria muito significado.
Assim, a forma mais correta de resolver as inequaçõespropostas, denominadas, respectivamente, de inequaçãoproduto e inequaçãoquociente, seria pensar da seguinte forma:
Assim, seria interessante conhecer os sinais dessas expressões, em ambos os casos, pois conhecemos as regras de sinais da multiplicação e da divisão. Conhecendo os sinais dessas expressões, podemos decidir quando o produto ou quociente serão positivos ou negativos.
Devemos então estudar o sinal das expressões, como se faz com as funções.
Voltemos aos exemplos:
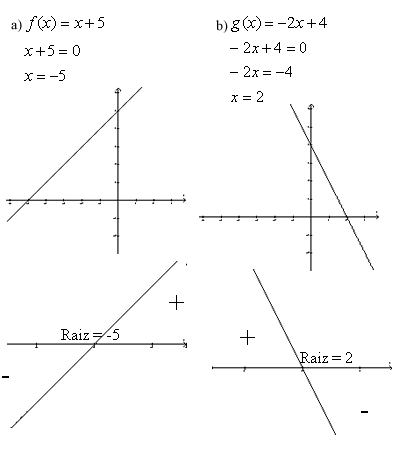 |
Depois de estudarmos os sinais das duas expressões, devemos analisar o sinal do produto das duas, pois é o que queremos. Assim, devemos colocar as duas funções no mesmo sistema de eixos. Uma forma mais prática e bastante utilizada de se fazer isso é utilizar o quadro de sinais ou "varal".
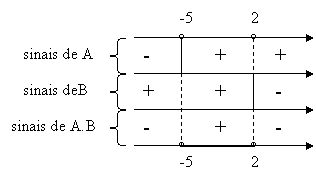 |
Assim, podemos fazer as regras de sinais, de acordo com o sinal de cada função, antes de -5, entre -5 e 2 e depois de 2.
Como nos interessa saber quando esse produto é positivo, destacamos o intervalo entre -5 e 2 - utilizando as notações adequadas de intervalos reais - pois foi onde isso aconteceu.
Logo, a solução dessa inequação é
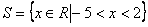 |
É importante destacar que -5 e 2 não fazem parte da solução, pois são valores onde as funções são nulas, e queremos os valores de x que tornam positivo o produto, não nulo. Isso fica representado no quadro de sinais pelo "buraco" na reta, nesses dois valores. E, na solução, isso fica representado pelo sinal de <, e não
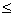 .
. Essa inequação poderia também ser resolvida se aplicássemos a propriedade distributiva, mas também por meio do estudo do sinal, nesse caso do estudo do sinal da função de segundo grau.
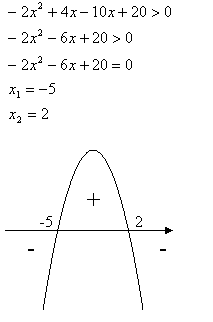 |
Percebemos que o estudo do sinal revela a mesma solução, ou seja, a função do segundo grau tem as mesmas raízes e os mesmos sinais que o produto das duas funções de primeiro grau estudadas anteriormente. Assim, interessa-nos o intervalo da reta real entre -5 e 2, onde a função é positiva.
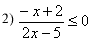 |
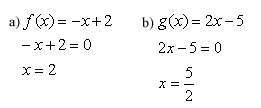 |
Sem precisar traçar os gráficos, podemos esboçá-los, conhecendo as raízes e o crescimento de cada uma, olhando para o sinal do coeficiente de x.
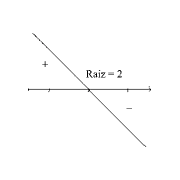
A) coeficiente de x = -1 < 0
Função decrescente
Raiz = 2
 |
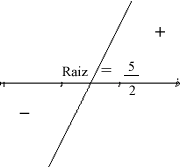
B) coeficiente de x = 2 > 0
Função crescente
Raiz =
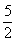
 |
Atenção: Não é o sinal da raiz que determina o crescimento ou decrescimento da função, mas o sinal do coeficiente de x. Esse é um erro bem comum! Cuidado!
Estudados os sinais, vamos ao quadro de sinais:
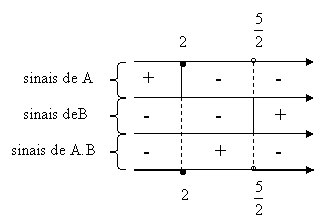 |
É importante notar: apesar de querermos os valores de x que tornam o quociente negativo ou nulo, não devemos incluir nunca na solução o valor de x que anula o denomidador da fração (a raiz da expressão do denominador), pois não existe fração com denominador nulo. Esse é outro erro comum!
Logo, a solução é
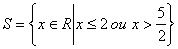 |
- Inequação Produto
Algumas inequações apresentam, no 1º membro, produto de funções que para obter a resolução dessas inequações é preciso fazer o estudo do sinal de todas as funções, a solução seria a intersecção do estudo dos sinais das funções que pertencem...
- Inequação Produto
Algumas inequações apresentam, no 1º membro, produto de funções que para obter a resolução dessas inequações é preciso fazer o estudo do sinal de todas as funções, a solução seria a intersecção do estudo dos sinais das funções que pertencem...
- Inequação De 2º Grau
Inequação do 2º grau na variável x é uma expressão matemática de desigualdade escrita nas seguintes formas redutíveis: ax² + bx + c > 0 ax² + bx + c < 0 ax² + bx + c ≥ 0 ax² + bx + c ≤ 0 onde a, b e c pertencem ao conjunto dos números...
- Inequação Produto
Inequação Produto Resolver uma inequação produto consiste em encontrar os valores de x que satisfazem a condição estabelecida pela inequação. Para isso utilizamos o estudo do sinal de uma função. Observe a resolução da seguinte equação produto:...
- Gráfico De Inequações Do 1º Grau
Diferente das equações, as inequações são expressões matemáticas que apresentam em sua configuração sinais de desigualdade. Veja: >: maior que <: menor que ≥: maior ou igual que ≤: menor ou igual que As inequações são utilizadas...
