Matemática
Os logaritmos criados por John Napier e Jobst Burgi, e posteriormente adaptados por Henry Briggs, possuem a seguinte lei de formação:
logab = x, onde:
a = base do logaritmo
b = logaritmando
x = logaritmo
O logaritmo de um número b em uma base a é o expoente x que se deve aplicar à base a para se ter o número b. Dessa forma:
logab = x ↔ ax = b
Exemplos:
log39 ↔ 32 = 9
log10100 ↔ 102 = 100
log216 ↔ 24 = 16
log981 ↔ 92 = 81
A partir dessa definição podemos apresentar algumas definições que auxiliarão no desenvolvimento de algumas situações envolvendo logaritmo. Veja:
O logaritmo do número 1 em qualquer base sempre será igual a 0.
loga1 = 0, pois a0 = 1
O logaritmo de qualquer número a na própria base a será igual a 1.
logaa = 1, pois a1 = a
O logaritmo de uma potência da base é o expoente, em qualquer base.
logaam = m, pois m * logaa = m * 1 = m
A potência de base a e expoente logab é igual a b.
alogab = b, pois logab = x → ax = b
Dois logaritmos são iguais, quando seus logaritmandos forem iguais.
logab = logac ↔ b = c
Exemplos
Aplicar a definição de logaritmo para calcular o valor de x em cada caso:
a) log327 = x → 3x = 27 → x = 3
b) log81x = 3/4 → x = 813/4 → x = (34)3/4 → x = 312/4 → x = 33 → x = 27
c) log4√2 = x → 4x = √2 → 22x = √2 → 22x = 21/2 → 2x = 1/2 → x = 1/4
d) logx8 = 2 → x2 = 8 → √x = √8 → x = 2√2
e) log4(2x – 1) = 1/2 → 2x – 1 = 41/2 → 2x – 1 = √4 → 2x – 1 = 2 → 2x = 3 → x = 3/2
f) log1818 = x → 18x = 18 → x = 1
g) logx1024 = 2 → x2 = 1024 → √x² = √1024 → x = 32
h) log40,25 = x → 4x = 0,25 → 4x = 25/100 → 4x = 1/4 → 4x = 4–1 → x = –1
i) 16log25 = (24)log25 = (2log25)4 = 54 = 625
j) log0,01 = x → 10x = 0,01 → 10x = 1/100 → 10x = 10–2 → x = –2Os logaritmos foram criados no intuito de facilitar os cálculos envolvendo números muito grandes ou muito pequenos. Os logaritmos reduzem esses números a algumas bases, a mais utilizada é a base decimal. As propriedades operatórias dos logaritmos possuem o objetivo de transformar multiplicações em somas, divisões em subtrações, potenciações em multiplicações e radiciações em divisões. Essas transformações facilitam os cálculos mais extensos.
Logaritmo de um produto
Considerando a, b e c números reais positivos e a ≠ 1, temos a seguinte propriedade:
loga(b*c) = logab + logac
Exemplo 1
Dados log2 = 0,301 e log3 = 0,477, determine o log12.
log12 → log12 = log(2 * 2 * 3) → log12 = log2 + log2 + log3 → log12 = 0,301 + 0,301 + 0,477 → log 12 = 1,079
Exemplo 2
Determine o valor de log2(8*32).
log2(8*32) = log28 + log232 = 3 + 5 = 8
Logaritmo de um quociente
Considerando a, b e c números reais positivos e a ≠ 1, temos a seguinte propriedade:
loga(b/c) = logab – logac
Exemplo 3
Sabendo que log30 = 1,477 e log5 = 0,699, determine log6.
log6 = (30/5) = log30 – log5 = 1,477 – 0,699 = 0,778
Exemplo 4
log3(6561/81) = log36561 – log381 = 8 – 4 = 5
Logaritmo de uma potência
Considerando a e b números reais positivos, com a ≠ 1, e m um número real, temos a seguinte propriedade:
logabm = m * logab
Exemplo 5
Sabendo que log 2 = 0,3010, calcule o valor de log 64.
log 64 = log 26 = 6 * log 2 = 6 * 0,3010 = 1,806
Exemplo 6
Dado log 2x = 2,4 e log 2 = 0,3, calcule x.
log 2x = 2,4 → x*log 2 = 2,4 → x * 0,3 = 2,4 → x = 2,4/0,3 → x = 8
Mudança de base
Para passarmos logab, com a e b positivos e a ≠ 1, para a base c, com c > 0 e c ≠ 1, utilizamos a seguinte expressão:
logab = logcb/ logca, com logca ≠ 0
Exemplo 7
Passando log49 para a base 2.
log49 = log29 / log24 = log29 / 2
Exemplo 8
Sabendo que log 4 = 0,60 e log 5 = 0,70, calcule log54.
log54 = log4 / log5 = 0,60 / 0,70 → log54 = 0,86
Transformando base e para a base decimal.
Considere o número real positivo x, para tal temos:
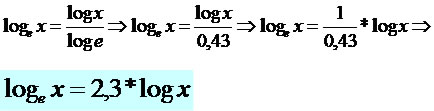
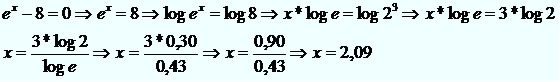
Exemplo 4
Calcular o valor de y na equação,
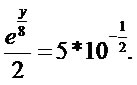
Resolução:
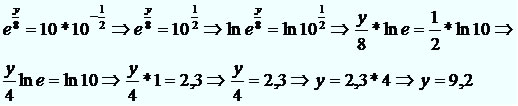
Exemplo 5
A corrente elétrica que atravessa um circuito é dada por i = 10 * e–0,02*t, em que i0 é o valor da corrente no instante t = 0 e i é o valor da corrente decorridos t segundos. Determine em quantos segundos a corrente atinge 2% do seu valor inicial. (dado: ln 0,02 = – 4)
Resolução: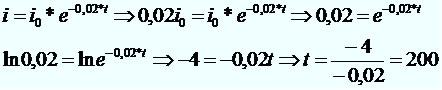
A corrente elétrica leva 200 segundos para atingir 2% do seu valor inicial.
www.mundoeducacao.com.br
- Logaritmo
Teoria dos Logaritmos 1. DEFINIÇÃO Sejam a e b números reais positivos diferentes de zero e b1. Chama-se logaritmo de a na base b o expoente x tal que bx = a: logb a = x bx = az Na sentença logb a = x temos: a) a é o logaritmando; b) b é a base...
- Equações Logaritmicas
Os logaritmos possuem várias aplicações na Matemática e em diversas áreas do conhecimento, como Física, Biologia, Química, Medicina, Geografia entre outras. Iremos através de exemplos demonstrar a utilização das técnicas de logaritmos na busca...
- Logaritmos
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com...
- Logaritmos
Os logaritmos criados por John Napier e Jobst Burgi, e posteriormente adaptados por Henry Briggs, possuem a seguinte lei de formação: logab = x, onde: a = base do logaritmo b = logaritmando x = logaritmo O logaritmo de um número b em uma base a é...
- Logaritmo
Os logaritmos criados por John Napier e Jobst Burgi, e posteriormente adaptados por Henry Briggs, possuem a seguinte lei de formação: logab = x, onde: a = base do logaritmo b = logaritmando x = logaritmo O logaritmo de um número b em uma base a é...
Matemática
Logaritmos
Os logaritmos criados por John Napier e Jobst Burgi, e posteriormente adaptados por Henry Briggs, possuem a seguinte lei de formação:
logab = x, onde:
a = base do logaritmo
b = logaritmando
x = logaritmo
O logaritmo de um número b em uma base a é o expoente x que se deve aplicar à base a para se ter o número b. Dessa forma:
logab = x ↔ ax = b
Exemplos:
log39 ↔ 32 = 9
log10100 ↔ 102 = 100
log216 ↔ 24 = 16
log981 ↔ 92 = 81
A partir dessa definição podemos apresentar algumas definições que auxiliarão no desenvolvimento de algumas situações envolvendo logaritmo. Veja:
O logaritmo do número 1 em qualquer base sempre será igual a 0.
loga1 = 0, pois a0 = 1
O logaritmo de qualquer número a na própria base a será igual a 1.
logaa = 1, pois a1 = a
O logaritmo de uma potência da base é o expoente, em qualquer base.
logaam = m, pois m * logaa = m * 1 = m
A potência de base a e expoente logab é igual a b.
alogab = b, pois logab = x → ax = b
Dois logaritmos são iguais, quando seus logaritmandos forem iguais.
logab = logac ↔ b = c
Exemplos
Aplicar a definição de logaritmo para calcular o valor de x em cada caso:
a) log327 = x → 3x = 27 → x = 3
b) log81x = 3/4 → x = 813/4 → x = (34)3/4 → x = 312/4 → x = 33 → x = 27
c) log4√2 = x → 4x = √2 → 22x = √2 → 22x = 21/2 → 2x = 1/2 → x = 1/4
d) logx8 = 2 → x2 = 8 → √x = √8 → x = 2√2
e) log4(2x – 1) = 1/2 → 2x – 1 = 41/2 → 2x – 1 = √4 → 2x – 1 = 2 → 2x = 3 → x = 3/2
f) log1818 = x → 18x = 18 → x = 1
g) logx1024 = 2 → x2 = 1024 → √x² = √1024 → x = 32
h) log40,25 = x → 4x = 0,25 → 4x = 25/100 → 4x = 1/4 → 4x = 4–1 → x = –1
i) 16log25 = (24)log25 = (2log25)4 = 54 = 625
j) log0,01 = x → 10x = 0,01 → 10x = 1/100 → 10x = 10–2 → x = –2Os logaritmos foram criados no intuito de facilitar os cálculos envolvendo números muito grandes ou muito pequenos. Os logaritmos reduzem esses números a algumas bases, a mais utilizada é a base decimal. As propriedades operatórias dos logaritmos possuem o objetivo de transformar multiplicações em somas, divisões em subtrações, potenciações em multiplicações e radiciações em divisões. Essas transformações facilitam os cálculos mais extensos.
Logaritmo de um produto
Considerando a, b e c números reais positivos e a ≠ 1, temos a seguinte propriedade:
loga(b*c) = logab + logac
Exemplo 1
Dados log2 = 0,301 e log3 = 0,477, determine o log12.
log12 → log12 = log(2 * 2 * 3) → log12 = log2 + log2 + log3 → log12 = 0,301 + 0,301 + 0,477 → log 12 = 1,079
Exemplo 2
Determine o valor de log2(8*32).
log2(8*32) = log28 + log232 = 3 + 5 = 8
Logaritmo de um quociente
Considerando a, b e c números reais positivos e a ≠ 1, temos a seguinte propriedade:
loga(b/c) = logab – logac
Exemplo 3
Sabendo que log30 = 1,477 e log5 = 0,699, determine log6.
log6 = (30/5) = log30 – log5 = 1,477 – 0,699 = 0,778
Exemplo 4
log3(6561/81) = log36561 – log381 = 8 – 4 = 5
Logaritmo de uma potência
Considerando a e b números reais positivos, com a ≠ 1, e m um número real, temos a seguinte propriedade:
logabm = m * logab
Exemplo 5
Sabendo que log 2 = 0,3010, calcule o valor de log 64.
log 64 = log 26 = 6 * log 2 = 6 * 0,3010 = 1,806
Exemplo 6
Dado log 2x = 2,4 e log 2 = 0,3, calcule x.
log 2x = 2,4 → x*log 2 = 2,4 → x * 0,3 = 2,4 → x = 2,4/0,3 → x = 8
Mudança de base
Para passarmos logab, com a e b positivos e a ≠ 1, para a base c, com c > 0 e c ≠ 1, utilizamos a seguinte expressão:
logab = logcb/ logca, com logca ≠ 0
Exemplo 7
Passando log49 para a base 2.
log49 = log29 / log24 = log29 / 2
Exemplo 8
Sabendo que log 4 = 0,60 e log 5 = 0,70, calcule log54.
log54 = log4 / log5 = 0,60 / 0,70 → log54 = 0,86
O sistema de logaritmos neperianos possui como base o número irracional e (e = 2,718...). Esse sistema também é conhecido como sistema de logaritmos naturais, com a condição x > 0. Ele pode ser expresso por:
logex = ln x
logex = ln x
Transformando base e para a base decimal.
Considere o número real positivo x, para tal temos:
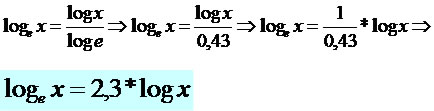
Através da relação demonstrada, podemos resolver os problemas propostos envolvendo a base decimal e a base e.
Exemplo 1
Sabendo que log 5 = 0,70, determine ln5.
Resolução:
ln x = 2,3 * log x → ln 5 = 2,3 * log 5 → ln 5 = 2,3 * 0,70 → ln 5 = 1,61
Exemplo 2
Sendo ln 0,02 = – 3,9, determine log 0,02.
Resolução:Se ln x = 2,3 * log x, então:
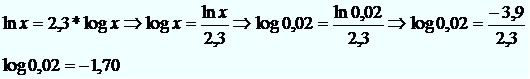
Exemplo 3
Dados log 2 = 0,30 e log e = 0,43, calcule o valor de x na equação ex – 8 = 0.
Resolução:
Exemplo 1
Sabendo que log 5 = 0,70, determine ln5.
Resolução:
ln x = 2,3 * log x → ln 5 = 2,3 * log 5 → ln 5 = 2,3 * 0,70 → ln 5 = 1,61
Exemplo 2
Sendo ln 0,02 = – 3,9, determine log 0,02.
Resolução:Se ln x = 2,3 * log x, então:
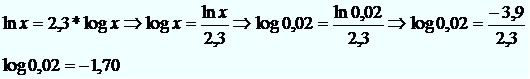
Exemplo 3
Dados log 2 = 0,30 e log e = 0,43, calcule o valor de x na equação ex – 8 = 0.
Resolução:
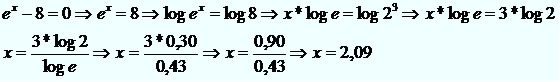
Exemplo 4
Calcular o valor de y na equação,
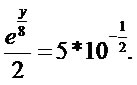
Resolução:
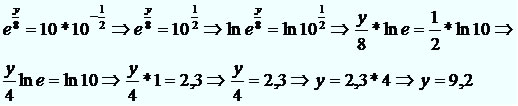
Exemplo 5
A corrente elétrica que atravessa um circuito é dada por i = 10 * e–0,02*t, em que i0 é o valor da corrente no instante t = 0 e i é o valor da corrente decorridos t segundos. Determine em quantos segundos a corrente atinge 2% do seu valor inicial. (dado: ln 0,02 = – 4)
Resolução:
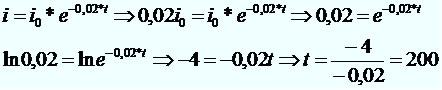
www.mundoeducacao.com.br
- Logaritmo
Teoria dos Logaritmos 1. DEFINIÇÃO Sejam a e b números reais positivos diferentes de zero e b1. Chama-se logaritmo de a na base b o expoente x tal que bx = a: logb a = x bx = az Na sentença logb a = x temos: a) a é o logaritmando; b) b é a base...
- Equações Logaritmicas
Os logaritmos possuem várias aplicações na Matemática e em diversas áreas do conhecimento, como Física, Biologia, Química, Medicina, Geografia entre outras. Iremos através de exemplos demonstrar a utilização das técnicas de logaritmos na busca...
- Logaritmos
Professor de Matemática e Biologia Antônio Carlos Carneiro BarrosoColégio Estadual Dinah Gonçalvesemail [email protected] www.ensinodematemtica.blogspot.com.brwww.accbarrosogestar.blogspot.com.br WWW.profantoniocarneiro.com...
- Logaritmos
Os logaritmos criados por John Napier e Jobst Burgi, e posteriormente adaptados por Henry Briggs, possuem a seguinte lei de formação: logab = x, onde: a = base do logaritmo b = logaritmando x = logaritmo O logaritmo de um número b em uma base a é...
- Logaritmo
Os logaritmos criados por John Napier e Jobst Burgi, e posteriormente adaptados por Henry Briggs, possuem a seguinte lei de formação: logab = x, onde: a = base do logaritmo b = logaritmando x = logaritmo O logaritmo de um número b em uma base a é...