Matemática

Matemática Através de Problemas - I

Oi, pessoal!

Pra quem acompanha o blog com certa frequência, sabe que tínhamos, antes da paralisação da atividade, uma Seção de Problemas, onde postávamos problemas separados pela área olímpica da qual pertenceriam. Desse modo, não postávamos problemas que envolvessem uma base teórica muito forte, mas sim apenas a vontade e a habilidade para se resolver problemas.

Porém, como sabemos, existem problemas extremamente difíceis para todo e qualquer tipo de conhecimento matemático, e isso causa que alguns dos desafios mais intrigantes da matemática sejam ignorados se nos restringirmos ao mundo elementar.

Portanto, não devemos ter mais uma Seção de Problemas, como antigamente. Devido às (pequenas!) divergências estilísticas dos dois autores, ambos vão enviar vez ou outra pequenas postagens, com o intuito de propor e, eventualmente, resolver problemas intrigantes, bonitos e desafiadores da matemática.

Assim, a parcela de contribuição do João para esse pequeno "projeto" de seções de problemas terá o título do Post: "Matemática Através de Problemas". Como esse é o primeiro, temos o "I" ao lado do nome :)

Espero que vocês gostem do novo estilo que estamos propondo.

Problema 1 - Seja N um número natural múltiplo de 9 tal que, ao ser escrito em base 10, existe um dígito tal que, se o retirarmos de N e considerarmos o inteiro assim formado, este será N/9, e ainda será múltiplo de 9.

(i) Prove que a divisão deste número novo por 9 é efetuada, também, retirando-se um de seus dígitos.

(ii) Encontre todos os números que têm tal propriedade.

Problema 2 (Equação Diferencial de Euler) - Seja u uma solução da equação diferencial parcial de Euler:

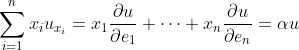
$\sum_{i=1}^n x_i u_{x_i} = x_1 \frac{\partial u}{\partial e_1}+\cdots + x_n \frac{\partial u}{\partial e_n} = \alpha u$

Mostre que u é homogênea de parâmetro alfa, ou seja, que

, para todo x em

. Reciprocamente, mostre que toda u homogênea de parâmetro alfa e de classe C ¹ satisfaz tal equação.

Problema 3 - (a) Sejam A, B dois conjuntos de medida não nula. Prove que o conjunto

$A+B = \{a+b, a \in A, b \in B \}$

Contém um intervalo.

(b) Use a parte (a) para provar que uma função mensurável

que satisfaz

$f(x+y) = f(x)+f(y) \;\; \forall\; x,y \in \mathbb{R}$

necessariamente é da forma

para algum c constante real. (A equação acima é a chamada equação de Cauchy, e tem generalizações para espaços muito mais gerais que a reta)

Problema 4 - Seja R um retângulo no plano. Suponha que R pode ser escrito como uma união

De retângulos com interiores disjuntos e com lados paralelos aos lados do retângulo original. Suponha também que cada um dos retângulos tem um lado de medida inteira. Prove que R tem um lado de medida inteira.

Problema 5 - Seja n um número natural. Mostre que existem números reais positivos

tais que os polinômios (tomados fazendo uma escolha de sinal)

Têm todas as raízes reais.

Dicas e Sugestões

Problema 1 - Analise as possibilidades para o dígito que foi retirado e veja que pode ser apenas um zero ou um nove. Uma das duas é impossível, e, na outra, é fácil determinar a posição do dígito, da esquerda pra direita: se

em expansão decimal, então mostre que o dígito retirado foi um zero e que foi o

.

Problema 2 - Para a primeira implicação, fixe um x e depois transforme a EDP numa EDO: defina

, encontre a EDO que esta função satisfaz e resolva. Para a segunda, derive os dois lados da igualdade em relação a

.

Problema 3 - (a) Reduza ao caso de medida finita primeiro. Depois, considere a convolução das características dos dois conjuntos e use as propriedades da convolução para concluir.

(b) Considere os conjuntos

. Pela suposição, são mensuráveis. Algum desses tem medida positiva (pois sua união é a reta), logo, seja

. Usando isto e o fato de que se f satisfaz a equação de Cauchy e é limitada em um intervalo, então ela é contínua, conclua.

Problema 4 - Calcule a integral

$\int_{R}e^{2i\pi(x_1 + x_2)}dx_1 dx_2$

de duas maneiras diferentes. Mais explicitamente, mostre que tal integral tem que resultar em zero, da condição dos retângulos menores terem um lado inteiro. Use isto para concluir.

Problema 5 - Indução. Se temos k números que satisfazem as propriedades, considere os polinômios obtidos multiplicando os que já tínhamos por x e trabalhe com estes.

Na próxima "edição" teremos mais alguns problemas interessantes. Além dos problemas daqui, estamos abertos a sugestões de problemas interessantes de outras Seções de Problemas que vocês querem ver solução, e também estamos abertos e encorajamos o envio de soluções de problemas por leitores. As melhores poderão ser escolhidas para aparecer na página.

- Matemática Através De Problemas - Vi
Oi, pessoal! Dada a falta de tempo dos administradores do blog, não estamos conseguindo postar muito conteúdo. Para compensar a falta de material novo, apresentamos aqui mais uma leva de problemas interessantes: 1 - Ache todas as funções contínuas...

- Matemática Através De Problemas - V
Olá, pessoal! Aqui vamos apresentar mais alguns problemas interessantes, e mostrar algumas soluções pros problemas propostos da ultima vez. Problemas Propostos 1 - (OMERJ-2011) Dada uma sequência de N inteiros não-negativos $a_j$ tal...

- Matemática Através De Problemas - Iv
Trazemos aqui mais uma seção de problemas interessantes: 1 - Seja f uma função real duas vezes diferenciável tal que, para todo x real, vale que Onde g é uma função mensurável e positiva. Prove que f é limitada. ...

- Desafio Da Semana
Olá, pessoal! Hoje venho propor uma nova seção, o Desafio da Semana. Toda semana vamos postar um problema desafiador, e, caso alguém mande soluções para nós, publicaremos as melhores aqui no blog, antes de propor o novo problema da semana! Então,...

- Equação De 2º Grau
1. Calcular o discriminante de cada equação e analisar as raízes em cada caso:a) x² + 9 x + 8 = 0 (R:-1 e -8) b) 9 x² - 24 x + 16 = 0 (R:4/3) c) x² - 2 x...

Matemática