Matemática
A busca de processos exatos ou mesmo aproximados para o cálculo de área $S$ da região limitada por uma curva fechada deu a Arquimedes (século $IIIa.C.$ aproximadamente) a glória de ser considerado um dos maiores matemáticos de todos os tempos. Com seu método da exaustão, conseguiu calcular áreas de regiões limitadas por inúmeros tipos de curvas.
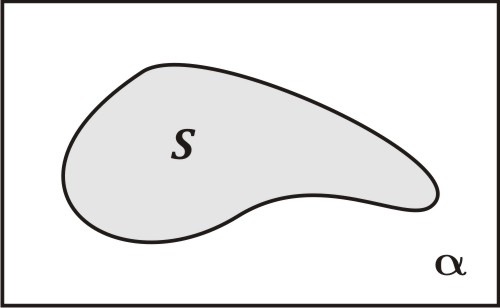
Após Arquimedes, só no século $XVII$, por volta de $1670$, é que o processo definitivo, com a invenção do Cálculo Integral, simultaneamente por Newton, na Inglaterra, e por Leibniz, na Alemanha.
A ideia do método é, resumidamente, a seguinte: seja $f(x)$ uma função contínua e "positiva" $(f(x) \geq 0)$ num intervalo $[a,b]$.

Vamos escolher no intervalo $[a,b]$ uma sequência de pontos, que chamaremos de sequência de partição:
\begin{equation}
P={a=x_0,x_1,x_2,\cdots , x_{n-1}, x_n=b}, \quad \text{sendo}\ n \geq 2
\end{equation}
com a condição:
\begin{equation}
a=x_0<x_1<x_2<\cdots <x_{n-1}<x_n=b
\end{equation}
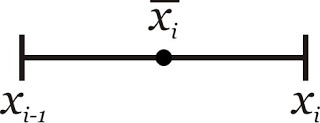
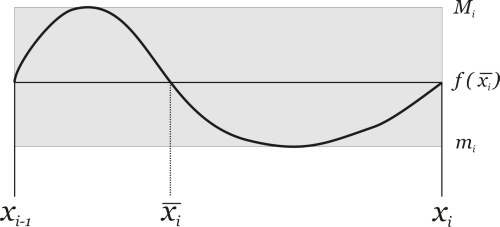
Cada intervalo terá a extensão $dx_i=x_i-x_{i-1}$, sendo $i=1,2,\cdots n$ e nesse i-ésimo intervalo a função $f$ terá os valores máximos e mínimos $M_i$ e $m_i$, respectivamente.
Escolhido um ponto amostral $\overline{x_i}$ nesse intervalo, a imagem $f(\overline{x_i})$ será com valor amostral de $f$.
A figura abaixo sugere os cálculos das seguintes áreas elementares:
\begin{equation}
m_idx_i, f(\overline{x_i}), M_idx_i
\end{equation}
Se variarmos o índice $i$ de $1$ a $n$, teremos os somatórios:
relativas à sequência de partição escolhida:
\begin{gather}
A_n = \sum_{i=1}^n m_idx_i \longrightarrow \text{Soma inferior}\\
B_n = \sum_{i=1}^n f(\overline{x_i})dx_i \longrightarrow \text{Soma amostral}\\
C_n = \sum_{i=1}^n M_idx_i \longrightarrow \text{Soma superior}
\end{gather}
Uma primeira propriedade dessas somas salta logo à vista:
\begin{equation}
A_n \leq B_n \leq C_n
\end{equation}
Isto decorre da desigualdade $m_i \leq f(\overline{x_i}) \leq M_i$ e das propriedades algébricas das desigualdades.
Esses números $A_n \leq B_n \leq C_n$ constituem atraentes aproximações da área $S$ procurada (da região entre a curva e o eixo dos $x$, no intervalo $[a,b]$).
É de esperar também que se procure melhorar as aproximações, como era feito por Arquimedes: aumentando muito, muito mesmo, o número $n$ de divisões de $[a,b]$, isto levando certamente ao uso da palavra limite na procura da aproximação ideal, aquela que deverá ser considerada como, por definição, o valor da área $S$.
Para alguns tipos de funções, sendo as mais importantes as contínuas, prova-se que existe um, e somente um, número real $S$, tal que:
\begin{equation}
S=\lim_{n\rightarrow \infty}A_n = \lim_{n \rightarrow \infty}B_n = \lim_{n \rightarrow \infty}C_n
\end{equation}
desde que em cada sequência de partição a máxima extensão $dx_i$ tenda a zero. Portanto:
\begin{equation}
S = \lim_{n \rightarrow \infty}\sum_{i=1}^n m_idx_i = \lim_{n \rightarrow \infty} \sum_{i=1}^n f(\overline{x_i})dx_i = \lim_{n \rightarrow \infty} \sum_{i=1}^n M_idx_i
\end{equation}
desde que $\max (dx_i) \rightarrow 0$ e que esses limites sejam de fato iguais, isto é, que $f(x)$ seja integrável em $[a,b]$.
Esse número $S$ recebeu o nome de Integral de $f(x)$ no intervalo $[a,b]$ e é indicado por:
\begin{equation}
S=\int_a^b f(x)dx
\end{equation}
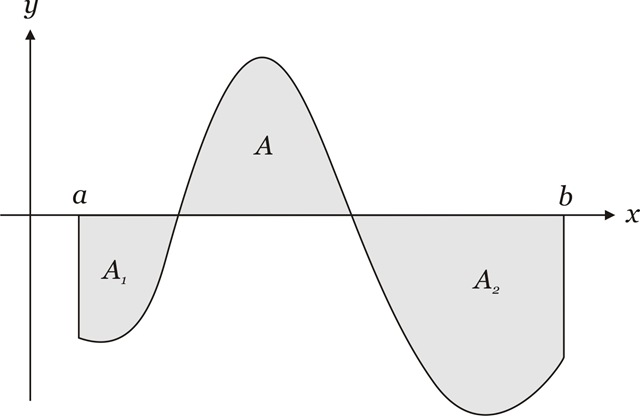
Se tiramos a condição $f(x) \geq 0$, a integral acima pode não representar a área entre a curva no intervalo $[a,b]$, como nos casos sugeridos pelas figuras seguintes:
$\displaystyle \bullet \int_a^b f(x)dx = -S$
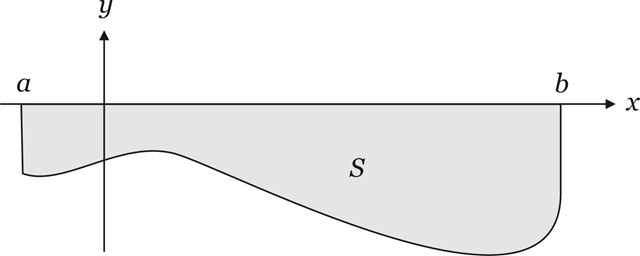
$\displaystyle \bullet \int_a^b f(x)dx = A-A_1-A_2$
Método de Integração por Substituição
Integração por substituição trigonométrica

- A Função Erro E Outras Funções Relacionadas
Por:Kleber KilhianPaulo Sérgio Costa Lino A função erro $erf(x)$ tem uma longa história que começa com os artigos de De Moivre $(1718-1733)$ e Laplace $(1774)$, onde foi expressa através da seguinte integral:$$\int e^{-t^2}dt$$ Mais tarde, Kramp...
- Integrais Impróprias Com Limites Finitos
Quando escrevemos uma integral definida como: \begin{equation} \int_a^b f(x)dx \end{equation} admitimos que o limite de integração são números finitos e que o integrando $f(x)$ é uma função contínua no intervalo limitado $a \leq x \leq b$. Sua...
- Demonstração Da Derivada Da Função Exponencial
Neste artigo, veremos como encontrar a derivada da função exponencial. Para isso utilizaremos limites e o conceito de derivada. Vamos demonstrar que, se $f(x)=e^x$, então sua derivada será $f '(x)=e^x$. Demonstração:Primeiramente, vamos provar...
- Demonstração Do Limite Fundamental Exponencial
O número e tem grande importância em diversos ramos das ciências, pois está presente em vários fenômenos naturais como por exemplo: crescimento populacional, crescimento de população de bactérias, datação por carbono, circuitos elétricos,...
- Demonstração Da Derivada Da Função Logarítmica
Neste artigo, veremos uma demonstração de como encontrar a derivada da função logarítmica usando o conceito de derivada e limites. Iremos provar que, se $ f(x) = \ln(x)$, então sua derivada será $\displaystyle f'(x) = \frac{1}{x}$. Demonstração:Seja...
Matemática
O Cálculo Integral: O Cálculo da Áreas
A busca de processos exatos ou mesmo aproximados para o cálculo de área $S$ da região limitada por uma curva fechada deu a Arquimedes (século $IIIa.C.$ aproximadamente) a glória de ser considerado um dos maiores matemáticos de todos os tempos. Com seu método da exaustão, conseguiu calcular áreas de regiões limitadas por inúmeros tipos de curvas.

Após Arquimedes, só no século $XVII$, por volta de $1670$, é que o processo definitivo, com a invenção do Cálculo Integral, simultaneamente por Newton, na Inglaterra, e por Leibniz, na Alemanha.
A ideia do método é, resumidamente, a seguinte: seja $f(x)$ uma função contínua e "positiva" $(f(x) \geq 0)$ num intervalo $[a,b]$.

Vamos escolher no intervalo $[a,b]$ uma sequência de pontos, que chamaremos de sequência de partição:
\begin{equation}
P={a=x_0,x_1,x_2,\cdots , x_{n-1}, x_n=b}, \quad \text{sendo}\ n \geq 2
\end{equation}
com a condição:
\begin{equation}
a=x_0<x_1<x_2<\cdots <x_{n-1}<x_n=b
\end{equation}
Cada intervalo terá a extensão $dx_i=x_i-x_{i-1}$, sendo $i=1,2,\cdots n$ e nesse i-ésimo intervalo a função $f$ terá os valores máximos e mínimos $M_i$ e $m_i$, respectivamente.
Escolhido um ponto amostral $\overline{x_i}$ nesse intervalo, a imagem $f(\overline{x_i})$ será com valor amostral de $f$.
A figura abaixo sugere os cálculos das seguintes áreas elementares:
\begin{equation}
m_idx_i, f(\overline{x_i}), M_idx_i
\end{equation}

Se variarmos o índice $i$ de $1$ a $n$, teremos os somatórios:

relativas à sequência de partição escolhida:
\begin{gather}
A_n = \sum_{i=1}^n m_idx_i \longrightarrow \text{Soma inferior}\\
B_n = \sum_{i=1}^n f(\overline{x_i})dx_i \longrightarrow \text{Soma amostral}\\
C_n = \sum_{i=1}^n M_idx_i \longrightarrow \text{Soma superior}
\end{gather}
Uma primeira propriedade dessas somas salta logo à vista:
\begin{equation}
A_n \leq B_n \leq C_n
\end{equation}
Isto decorre da desigualdade $m_i \leq f(\overline{x_i}) \leq M_i$ e das propriedades algébricas das desigualdades.
Esses números $A_n \leq B_n \leq C_n$ constituem atraentes aproximações da área $S$ procurada (da região entre a curva e o eixo dos $x$, no intervalo $[a,b]$).
É de esperar também que se procure melhorar as aproximações, como era feito por Arquimedes: aumentando muito, muito mesmo, o número $n$ de divisões de $[a,b]$, isto levando certamente ao uso da palavra limite na procura da aproximação ideal, aquela que deverá ser considerada como, por definição, o valor da área $S$.
Para alguns tipos de funções, sendo as mais importantes as contínuas, prova-se que existe um, e somente um, número real $S$, tal que:
\begin{equation}
S=\lim_{n\rightarrow \infty}A_n = \lim_{n \rightarrow \infty}B_n = \lim_{n \rightarrow \infty}C_n
\end{equation}
desde que em cada sequência de partição a máxima extensão $dx_i$ tenda a zero. Portanto:
\begin{equation}
S = \lim_{n \rightarrow \infty}\sum_{i=1}^n m_idx_i = \lim_{n \rightarrow \infty} \sum_{i=1}^n f(\overline{x_i})dx_i = \lim_{n \rightarrow \infty} \sum_{i=1}^n M_idx_i
\end{equation}
desde que $\max (dx_i) \rightarrow 0$ e que esses limites sejam de fato iguais, isto é, que $f(x)$ seja integrável em $[a,b]$.
Esse número $S$ recebeu o nome de Integral de $f(x)$ no intervalo $[a,b]$ e é indicado por:
\begin{equation}
S=\int_a^b f(x)dx
\end{equation}
Se tiramos a condição $f(x) \geq 0$, a integral acima pode não representar a área entre a curva no intervalo $[a,b]$, como nos casos sugeridos pelas figuras seguintes:
$\displaystyle \bullet \int_a^b f(x)dx = -S$

$\displaystyle \bullet \int_a^b f(x)dx = A-A_1-A_2$

Referências
[1] Cálculo 1 - Luiz Mauro Rocha - Ed. Atlas, 1987Veja mais
Método de Integração por PartesMétodo de Integração por Substituição
Integração por substituição trigonométrica
Atualização
Post atualizado em 22/11/2015
- A Função Erro E Outras Funções Relacionadas
Por:Kleber KilhianPaulo Sérgio Costa Lino A função erro $erf(x)$ tem uma longa história que começa com os artigos de De Moivre $(1718-1733)$ e Laplace $(1774)$, onde foi expressa através da seguinte integral:$$\int e^{-t^2}dt$$ Mais tarde, Kramp...
- Integrais Impróprias Com Limites Finitos
Quando escrevemos uma integral definida como: \begin{equation} \int_a^b f(x)dx \end{equation} admitimos que o limite de integração são números finitos e que o integrando $f(x)$ é uma função contínua no intervalo limitado $a \leq x \leq b$. Sua...
- Demonstração Da Derivada Da Função Exponencial
Neste artigo, veremos como encontrar a derivada da função exponencial. Para isso utilizaremos limites e o conceito de derivada. Vamos demonstrar que, se $f(x)=e^x$, então sua derivada será $f '(x)=e^x$. Demonstração:Primeiramente, vamos provar...
- Demonstração Do Limite Fundamental Exponencial
O número e tem grande importância em diversos ramos das ciências, pois está presente em vários fenômenos naturais como por exemplo: crescimento populacional, crescimento de população de bactérias, datação por carbono, circuitos elétricos,...
- Demonstração Da Derivada Da Função Logarítmica
Neste artigo, veremos uma demonstração de como encontrar a derivada da função logarítmica usando o conceito de derivada e limites. Iremos provar que, se $ f(x) = \ln(x)$, então sua derivada será $\displaystyle f'(x) = \frac{1}{x}$. Demonstração:Seja...
