Matemática


cujo valor é aproximadamente 2,718 281 828 459 045 235 360 287.
Aqui n! representa o fatorial de n.
A função ex (função exponencial de base e) pode ser representada da seguinte forma:
Ou, de forma mais simplificada (sequência [[OEIS:{{{1}}}|{{{1}}}]] na OEIS):
que pode ser escrita mais harmoniozamente com a utilização do zero:
- Prova De Irracionalidade Do Número De Euler
Na matemática, o número de Euler é uma das mais importantes constantes reais. A demonstração de que este número é irracional é considerada um dos mais elegantes teoremas de matemática. A demonstração baseia-se...
- Conjectura De Goldbach, O Que é?
A conjectura de Goldbach afirma que todo número par maior que 2 pode ser escrito como a soma de primos. Veja alguns exemplos: 4 = 2 + 2 48 = 41 + 7 12 = 5 +...
- O Número π (pi) E O Seu Dia
Hoje vou falar sobre o π (pi), você já o conhece? Pois bem, saiba que π (pi) é um número irracional e transcendente, que representa o quociente entre o perímetro de uma circunferência e o seu diâmetro, matematicando: se uma circunferencia tem...
- A Existência De "e"
Nesse post iremos tratar do famoso número de Euler , assim chamado em homenagem ao matemático suiço Leonard Euler, e o mesmo é a base dos logaritmos naturais. Iremos mostrar sua existência e que é limitado, . Definimos como sendo...
- A Mediana De Euler
Leonhard Euler $(1707-1783)$ foi um dos maiores matemáticos (ou o maior) do século $XVIII$, pois sua obra é impressionante, pela quantidade e pela diversidade. Dentre algumas áreas em que Euler contribuiu, podemos citar a Álgebra, Teoria dos Números,...
Matemática
O Número de Euler

Fonte: http://pt.wikipedia.org/
Na matemática , número de Euler, assim chamado em homenagem ao matemático suíço Leonhard Euler, é a base dos logaritmos naturais. As variantes do nome do número incluem: número de Napier, constante de Néper, número neperiano, constante matemática e número exponencial, etc.
O número e é um número irracional e mesmo transcendente (como pi). A irracionalidade de e foi demonstrada por Lambert em 1761 e mais tarde por Euler. A prova da transcendência de e foi estabelecida por Hermite em 1873. Conjecturou-se que e é um número normal ou aleatório. Ele aparece (com outras constantes fundamentais) na identidade de Euler, considerada a expressão mais "bela" da matemática:
Leonhard Euler começou a usar a letra e para representar a constante em 1727, e o primeiro uso de e foi na publicação Euler?s Mechanica (1736). As verdadeiras razões para escolha da letra são desconhecidas, mas especula-se que seja porque e é a primeira letra da palavra exponencial.
Outra aparição do número de Euler é na probabilidade: caso se escolham números entre zero e 1 até que o seu total ultrapasse 1, o número mais provável de seleções será igual a e.
A primeira referência à constante foi publicada em 1618 na tabela de um apêndice de um trabalho sobre logaritmos de John Napier. No entanto, este não contém a constante propriamente dita, mas apenas uma simples lista de logaritmos naturais calculados a partir desta. A primeira indicação da constante foi descoberta por Jakob Bernoulli, quando tentava encontrar um valor para a seguinte expressão (muito comum no cálculo de juros compostos):

cujo valor é aproximadamente 2,718 281 828 459 045 235 360 287.
Caracterizações Menos Triviais do Número de Euler
O número e pode ser representado e calculado por meio da utilização da série de Taylor para ex quando x=1, como a soma da seguinte série infinita:
Aqui n! representa o fatorial de n.
A função ex (função exponencial de base e) pode ser representada da seguinte forma:
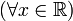 , exp(x) = ex
, exp(x) = ex
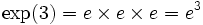 ou ainda
ou ainda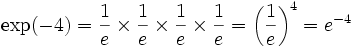
Ou, de forma mais simplificada (sequência [[OEIS:{{{1}}}|{{{1}}}]] na OEIS):
que pode ser escrita mais harmoniozamente com a utilização do zero:
Muitas outras séries, seqüências, frações contínuas e produtos infinitos que representam e já foram desenvolvidas.
O Número de Euler no Cálculo
A função exponencial y = ex tem a intrigante propriedade de ser sua própria derivada, i.e.:Isto significa que e tem a notável propriedade de que a taxa de variação de ex no ponto x = t vale et. Daí sua importância no cálculo diferencial e integral, e seu papel único como base do logaritmo natural. Além desta, pela regra da multiplicação por constante, as funções y = kex, 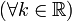 também são suas próprias derivadas.
também são suas próprias derivadas.
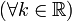 também são suas próprias derivadas.
também são suas próprias derivadas.Trabalhando com integrais, pode-se ainda definir e como sendo o único número maior que zero tal que:
Número de Euler como Séries Infinitas
Dentre as várias séries infinitas que resultam em e, têm-se, além da trivial:Número de Euler Como Limites e Produtos Infinitos
Os produtos infinitos:e
- O Número de Euler com os primeiros 510 dígitos decimais;
- Prova De Irracionalidade Do Número De Euler
Na matemática, o número de Euler é uma das mais importantes constantes reais. A demonstração de que este número é irracional é considerada um dos mais elegantes teoremas de matemática. A demonstração baseia-se...
- Conjectura De Goldbach, O Que é?
A conjectura de Goldbach afirma que todo número par maior que 2 pode ser escrito como a soma de primos. Veja alguns exemplos: 4 = 2 + 2 48 = 41 + 7 12 = 5 +...
- O Número π (pi) E O Seu Dia
Hoje vou falar sobre o π (pi), você já o conhece? Pois bem, saiba que π (pi) é um número irracional e transcendente, que representa o quociente entre o perímetro de uma circunferência e o seu diâmetro, matematicando: se uma circunferencia tem...
- A Existência De "e"
Nesse post iremos tratar do famoso número de Euler , assim chamado em homenagem ao matemático suiço Leonard Euler, e o mesmo é a base dos logaritmos naturais. Iremos mostrar sua existência e que é limitado, . Definimos como sendo...
- A Mediana De Euler
Leonhard Euler $(1707-1783)$ foi um dos maiores matemáticos (ou o maior) do século $XVIII$, pois sua obra é impressionante, pela quantidade e pela diversidade. Dentre algumas áreas em que Euler contribuiu, podemos citar a Álgebra, Teoria dos Números,...

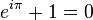
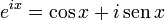
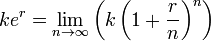
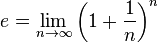
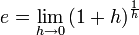
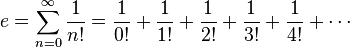
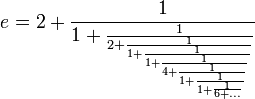
![e = [[2; 1, \textbf{2}, 1, 1, \textbf{4}, 1, 1, \textbf{6}, 1, 1, \textbf{8}, 1, 1, \ldots, \textbf{2n}, 1, 1, \ldots]], \,](matematica/matematica-5631d2107cc39.png)
![e = [[ 1 , \textbf{0} , 1 , 1, \textbf{2}, 1, 1, \textbf{4}, 1 , 1 , \textbf{6}, 1, 1, \textbf{8}, 1, 1, \ldots]], \,](matematica/matematica-5631d210c0243.png)
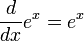
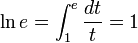
![e = \left [ \sum_{k=0}^\infty \frac{(-1)^k}{k!} \right ]^{-1}](matematica/matematica-5631d211bf29b.png)
![e = \left [ \sum_{k=0}^\infty \frac{1-2k}{(2k)!} \right ]^{-1}](matematica/matematica-5631d21203a1c.png)
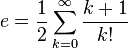
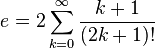
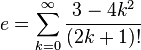
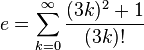
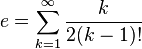
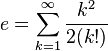
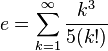
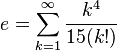
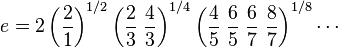
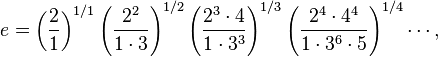
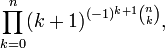
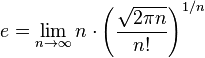
![e=\lim_{n \to \infty} \frac{n}{\sqrt[n]{n!}}](matematica/matematica-5631d2155c74d.png)
![e=\lim_{n \to \infty} \left [ \frac{(n+1)^{n+1}}{n^n}- \frac{n^n}{(n-1)^{n-1}} \right ]](matematica/matematica-5631d215a5c67.png)