Matemática
Um sistema de coordenadas no plano permite-nos associar um par ordenado de números a cada ponto do plano. Essa ideia simples e profunda que surgiu nos trabalhos dos matemáticos René Descartes e Pierre de Fermat, no século $XVII$ permite juntamente com o Cálculo investigar as propriedades das curvas através das ferramentas da Álgebra.

Na maioria dos casos, é abordado apenas o sistema de coordenadas retangulares ou cartesianas, no qual a ênfase é colocada sobre as distâncias de um ponto a dois eixos perpendiculares. Em algumas aplicações, tais como a curva descrita por um planeta em torno do sol, é mais vantajoso usar um outro sistema de coordenadas cuja posição de um ponto é descrito por sua direção a partir da origem, e por sua distância da origem. Um tal sistema é chamado de sistema de coordenadas polares.
Na figura acima, temos um ponto $P$ juntamente com suas coordenadas. A semirreta $OA$ é chamado eixo polar e $OP = r$ é o raio vetor. A direção especificada por um ângulo $\theta$ em radianos, medida a partir de $OA$. Este ângulo $\theta$ é positivo se for medido no sentido anti-horário e negativo se for medido no sentido horário exatamente como se faz na Trigonometria. A distância é dada pela distância orientada $r$, medida a partir da origem ao longo do lado terminal do ângulo $\theta$. Os dois números $r$ e $\theta$ escritos nesta ordem e denotados por $(r,\theta)$ chamam-se coordenadas polares do ponto. Observe que a semirreta $\theta = 0$ é o semi-eixo positivo dos $x$ e $\theta = \pi/2$ é o semi-eixo positivo dos $y$ e $r = 0$ indica-se a origem ou polo do sistema de coordenadas polares.
O termo "distância orientada" é devido ao fato de que em algumas situações encontramos $r$ negativo. Nesse caso, subentende-se que em vez de sair da origem no sentido indicado pelo lado terminal de $\theta$ nos dirigimos para a origem a ponto, percorrendo uma distância $r$ no sentido oposto a ele. Para compreender melhor este caso observe a figura abaixo.
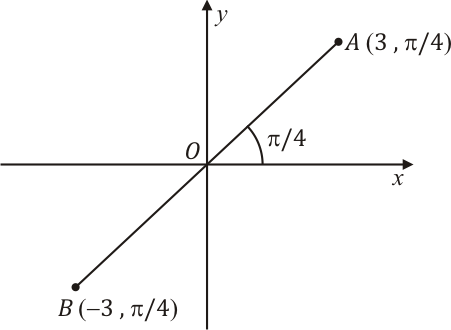
Podemos associar o sistema de coordenadas polares com o sistema de coordenadas cartesianas colocando o eixo polar sobre o eixo $x$, de modo que eixo polar $OA$ aponte para o sentido positivo do eixo $x$ como na figura acima. Nesta figura, o ponto $A$ possui coordenadas $(3,\pi/4)$, mas este ponto também tem coordenadas polares dadas por $A(3,\pi/4 + 2\pi)$. Assim, todo múltiplo de $2\pi$ somado ou subtraído da coordenada $\theta$ de um ponto produz um outro ângulo com o mesmo lado terminal; portanto, temos uma outra coordenada $\theta$ do mesmo ponto.
Simmons comenta em seu livro de Cálculo com Geometria Analítica que: "o fato de que um ponto não é representado por um único par de coordenadas polares é um aborrecimento, embora pequeno. Contudo, é verdade que qualquer par de coordenadas polares dado determina o correspondente ponto sem nenhuma ambiguidade."
Agora, já temos dois sistemas de coordenadas no plano e próximo passo é descobrir o modo de transformar as coordenadas de um sistema nas coordenadas do outro e vice-versa. Para isso, considere a figura abaixo:

Do triângulo retângulo, temos $\cos (\theta) = \cfrac{x}{r}$ e $\text{sen} (\theta) = \cfrac{y}{r}$. Assim, para transformar coordenadas polares em coordenadas cartesianas, usamos as expressões:
\begin{cases}
x = r\cos (\theta)\\
y = r\ \text{sen} (\theta)
\end{cases}
Novamente deste triângulo retângulo, temos
\begin{equation*}
\text{tg} (\theta) = \frac{y}{x} \Longrightarrow \theta = \text{arctg} \left(\frac{y}{x}\right)
\end{equation*}
e pelo teorema de Pitágoras,
\begin{equation*}
x^2 + y^2 = r^2
\end{equation*}
Estas expressões nos fornece o caminho para transformar coordenadas cartesianas em polares, isto é,
\begin{cases}
\theta = \text{arctg} \left(\cfrac{y}{x}\right)\\
r = \sqrt{x^2 + y^2}
\end{cases}
$a)$ $(3,4)$ para coordenadas polares;
$b)$ $(2,\pi/3)$ para coordenadas cartesianas.
Resolução:
$a)$ Neste caso, $r = \sqrt{3^2 + 4^2} = 5$ e $\text{tg} (\theta) = \cfrac{4}{3} \Longrightarrow \theta = \text{arctg}\left(\cfrac{4}{3}\right)$.
$b)$ Analogamente, usando as expressões acima, temos
\begin{equation*}
x = 2\cos \left(\frac{\pi}{3}\right) = 2\cdot \frac{1}{2} = 1
\end{equation*}
e
\begin{equation*}
y = 2~\text{sen} \left(\frac{\pi}{3}\right) = \sqrt{3}
\end{equation*}
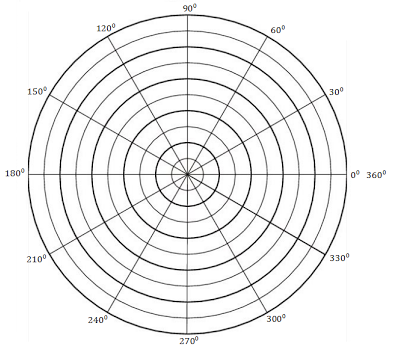
Se o raio vetor $r$ está relacionado com $\theta$ através da expressão $r = f(\theta)$, então se a função $f(\theta)$ é razoavelmente simples, podemos esboçar o seu gráfico escolhendo uma sequência adequada de valores de $\theta$ e calculando os valores correspondentes de $r$. O gráfico polar abaixo nos auxilia nesta tarefa.
Outros gráficos podem ser gerados desta forma, tais como circunferências, limaçons, lemniscatas, espirais, rosáceas, entre outros.
* Este artigo é uma republicação. O link do artigo original encontra-se nas referências.
Área em coordenadas polares
Centro de gravidade de áreas planas

- Desafio Resolvido
Parabéns Romero Morais conseguiu resolver este desafio! Resolução: Temos: $$N = P_y = m.g cos\theta$$ $$Fat = \mu . N = \mu . m.g.cos\theta$$ $$P_x = m.g.sen\theta$$ $$d$$ é a distância genérica percorrida pelo bloco. Trabalho na ida: $$\tau_T...
- Desafio - Física
Na figura, um bloco sobe um plano inclinado, com velocidade inicial $$V_0$$. Considere $$\mu$$ o coeficiente de atrito entre o bloco e a superfície. Indique sua velocidade ao passar pela posição inicial. A. $$V_0\sqrt{\frac{sen\theta - \mu cos\theta}{sen\theta...
- Integral De $\displaystyle \frac{\sqrt{16-x^2}}{4x^2}dx$
Às vezes surgem dúvidas de leitores que valem um post. A resolução desta integral é interessante e usa o método de substituição trigonométrica. Seja a integral: \begin{equation*} \int \frac{\sqrt{16-x^2}}{4x^2}dx = I \end{equation*} Vejam o artigo...
- Retas Perpendiculares
Veremos nesta postagem como determinar se duas retas são perpendiculares entre si, dados seus coeficientes angulares.Considere duas retas $r_1$ e $r_2$ não perpendiculares a nenhum dos eixos $x$ e $y$. Sejam $m_1$ e $m_2$ os coeficientes angulares das...
- Demonstração Da Relação Trigonométrica Fundamental
Nesta artigo, veremos como encontrar a relação trigonométrica fundamental no círculo trigonométrico utilizando o teorema de Pitágoras. Considere o círculo trigonométrico abaixo de raio unitário: O ponto $C$ é um ponto genérico sobre a circunferência...
Matemática
O sistema de coordenadas polares
Um sistema de coordenadas no plano permite-nos associar um par ordenado de números a cada ponto do plano. Essa ideia simples e profunda que surgiu nos trabalhos dos matemáticos René Descartes e Pierre de Fermat, no século $XVII$ permite juntamente com o Cálculo investigar as propriedades das curvas através das ferramentas da Álgebra.

Na maioria dos casos, é abordado apenas o sistema de coordenadas retangulares ou cartesianas, no qual a ênfase é colocada sobre as distâncias de um ponto a dois eixos perpendiculares. Em algumas aplicações, tais como a curva descrita por um planeta em torno do sol, é mais vantajoso usar um outro sistema de coordenadas cuja posição de um ponto é descrito por sua direção a partir da origem, e por sua distância da origem. Um tal sistema é chamado de sistema de coordenadas polares.
Na figura acima, temos um ponto $P$ juntamente com suas coordenadas. A semirreta $OA$ é chamado eixo polar e $OP = r$ é o raio vetor. A direção especificada por um ângulo $\theta$ em radianos, medida a partir de $OA$. Este ângulo $\theta$ é positivo se for medido no sentido anti-horário e negativo se for medido no sentido horário exatamente como se faz na Trigonometria. A distância é dada pela distância orientada $r$, medida a partir da origem ao longo do lado terminal do ângulo $\theta$. Os dois números $r$ e $\theta$ escritos nesta ordem e denotados por $(r,\theta)$ chamam-se coordenadas polares do ponto. Observe que a semirreta $\theta = 0$ é o semi-eixo positivo dos $x$ e $\theta = \pi/2$ é o semi-eixo positivo dos $y$ e $r = 0$ indica-se a origem ou polo do sistema de coordenadas polares.
O termo "distância orientada" é devido ao fato de que em algumas situações encontramos $r$ negativo. Nesse caso, subentende-se que em vez de sair da origem no sentido indicado pelo lado terminal de $\theta$ nos dirigimos para a origem a ponto, percorrendo uma distância $r$ no sentido oposto a ele. Para compreender melhor este caso observe a figura abaixo.

Podemos associar o sistema de coordenadas polares com o sistema de coordenadas cartesianas colocando o eixo polar sobre o eixo $x$, de modo que eixo polar $OA$ aponte para o sentido positivo do eixo $x$ como na figura acima. Nesta figura, o ponto $A$ possui coordenadas $(3,\pi/4)$, mas este ponto também tem coordenadas polares dadas por $A(3,\pi/4 + 2\pi)$. Assim, todo múltiplo de $2\pi$ somado ou subtraído da coordenada $\theta$ de um ponto produz um outro ângulo com o mesmo lado terminal; portanto, temos uma outra coordenada $\theta$ do mesmo ponto.
Simmons comenta em seu livro de Cálculo com Geometria Analítica que: "o fato de que um ponto não é representado por um único par de coordenadas polares é um aborrecimento, embora pequeno. Contudo, é verdade que qualquer par de coordenadas polares dado determina o correspondente ponto sem nenhuma ambiguidade."
Agora, já temos dois sistemas de coordenadas no plano e próximo passo é descobrir o modo de transformar as coordenadas de um sistema nas coordenadas do outro e vice-versa. Para isso, considere a figura abaixo:

Do triângulo retângulo, temos $\cos (\theta) = \cfrac{x}{r}$ e $\text{sen} (\theta) = \cfrac{y}{r}$. Assim, para transformar coordenadas polares em coordenadas cartesianas, usamos as expressões:
\begin{cases}
x = r\cos (\theta)\\
y = r\ \text{sen} (\theta)
\end{cases}
Novamente deste triângulo retângulo, temos
\begin{equation*}
\text{tg} (\theta) = \frac{y}{x} \Longrightarrow \theta = \text{arctg} \left(\frac{y}{x}\right)
\end{equation*}
e pelo teorema de Pitágoras,
\begin{equation*}
x^2 + y^2 = r^2
\end{equation*}
Estas expressões nos fornece o caminho para transformar coordenadas cartesianas em polares, isto é,
\begin{cases}
\theta = \text{arctg} \left(\cfrac{y}{x}\right)\\
r = \sqrt{x^2 + y^2}
\end{cases}
Exemplo $1$:
Transforme:$a)$ $(3,4)$ para coordenadas polares;
$b)$ $(2,\pi/3)$ para coordenadas cartesianas.
Resolução:
$a)$ Neste caso, $r = \sqrt{3^2 + 4^2} = 5$ e $\text{tg} (\theta) = \cfrac{4}{3} \Longrightarrow \theta = \text{arctg}\left(\cfrac{4}{3}\right)$.
$b)$ Analogamente, usando as expressões acima, temos
\begin{equation*}
x = 2\cos \left(\frac{\pi}{3}\right) = 2\cdot \frac{1}{2} = 1
\end{equation*}
e
\begin{equation*}
y = 2~\text{sen} \left(\frac{\pi}{3}\right) = \sqrt{3}
\end{equation*}
Se o raio vetor $r$ está relacionado com $\theta$ através da expressão $r = f(\theta)$, então se a função $f(\theta)$ é razoavelmente simples, podemos esboçar o seu gráfico escolhendo uma sequência adequada de valores de $\theta$ e calculando os valores correspondentes de $r$. O gráfico polar abaixo nos auxilia nesta tarefa.

Exemplo $2$:
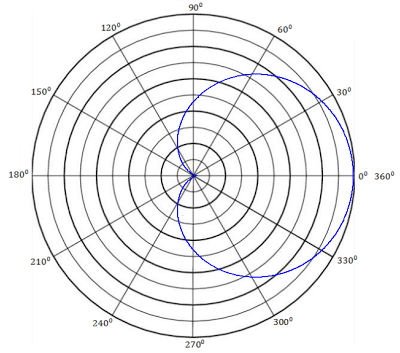
A curva cuja equação polar é $r = 2~(1 + \cos (\theta))$ é conhecida por cardioide (coração em latim). Sua representação no gráfico polar é dada na figura abaixo.
Outros gráficos podem ser gerados desta forma, tais como circunferências, limaçons, lemniscatas, espirais, rosáceas, entre outros.
* Este artigo é uma republicação. O link do artigo original encontra-se nas referências.
Referências:
[1] O sistema de coordenadas Polares no blog Fatos Matemáticos, originalmente escrito pelo prof. Paulo Sérgio C. LinoVeja mais:
Números complexosÁrea em coordenadas polares
Centro de gravidade de áreas planas

- Desafio Resolvido
Parabéns Romero Morais conseguiu resolver este desafio! Resolução: Temos: $$N = P_y = m.g cos\theta$$ $$Fat = \mu . N = \mu . m.g.cos\theta$$ $$P_x = m.g.sen\theta$$ $$d$$ é a distância genérica percorrida pelo bloco. Trabalho na ida: $$\tau_T...
- Desafio - Física
Na figura, um bloco sobe um plano inclinado, com velocidade inicial $$V_0$$. Considere $$\mu$$ o coeficiente de atrito entre o bloco e a superfície. Indique sua velocidade ao passar pela posição inicial. A. $$V_0\sqrt{\frac{sen\theta - \mu cos\theta}{sen\theta...
- Integral De $\displaystyle \frac{\sqrt{16-x^2}}{4x^2}dx$
Às vezes surgem dúvidas de leitores que valem um post. A resolução desta integral é interessante e usa o método de substituição trigonométrica. Seja a integral: \begin{equation*} \int \frac{\sqrt{16-x^2}}{4x^2}dx = I \end{equation*} Vejam o artigo...
- Retas Perpendiculares
Veremos nesta postagem como determinar se duas retas são perpendiculares entre si, dados seus coeficientes angulares.Considere duas retas $r_1$ e $r_2$ não perpendiculares a nenhum dos eixos $x$ e $y$. Sejam $m_1$ e $m_2$ os coeficientes angulares das...
- Demonstração Da Relação Trigonométrica Fundamental
Nesta artigo, veremos como encontrar a relação trigonométrica fundamental no círculo trigonométrico utilizando o teorema de Pitágoras. Considere o círculo trigonométrico abaixo de raio unitário: O ponto $C$ é um ponto genérico sobre a circunferência...
