Matemática
Romero Morais conseguiu resolver este desafio!

Resolução:
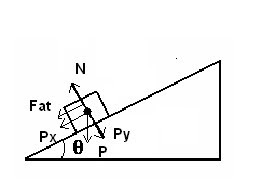
Temos:
$$N = P_y = m.g cos\theta$$
$$Fat = \mu . N = \mu . m.g.cos\theta$$
$$P_x = m.g.sen\theta$$
$$d$$ é a distância genérica percorrida pelo bloco.
Trabalho na ida:
$$\tau_T = \Delta{E_c}$$
$$\tau_{Fat} + \tau_{P_x} + \tau_{P_y} + \tau_N = E_{cF} - E_{cI}$$
$$\tau_{Fat} + \tau_{P_x} + E_{cF} = E_{cF} - E_{cI}$$
$$\tau_{Fat} + \tau_{P_x} = -E_{cI}$$
$$-\mu . m.g.cos\theta . d - m.g.sen\theta.d = -\frac{m.v^2}{2}$$
$$d = \frac{v^2}{2g(\mu cos\theta + sen\theta)}$$
Trabalho na volta:
$$\tau_T = \Delta{E_c}$$
$$\tau_{Fat} + \tau_{P_x} + \tau_{P_y} + \tau_N = E_{cF} - E_{cI}$$
$$\tau_{Fat} + \tau_{P_x} - E_{cI} = E_{cF} - E_{cI}$$
$$\tau_{Fat} +\tau_{P_x} = E_{cF}$$
$$-\mu.m.g.cos\theta.d + m.g.sen\theta.d = \frac{m.v^2}{2}(\div m)$$
$$-\mu.g.cos\theta \left[ \frac{V_0^2}{2g(\mu.cos\theta + sen\theta)}\right] + g.sen\theta \left[ \frac{V_0^2}{2g(\mu cos\theta + sen\theta)}\right] = \frac{V^2}{2}$$
$$V = V_0\sqrt{\frac{sen\theta - \mu cos\theta}{sen\theta + \mu cos\theta}}$$
Alternativa B.
- O Ciclo Trigonométrico
A definição das funções trigonométricas pode ser generalizada para um ângulo real qualquer através do ciclo trigonométrico. O ciclo trigonométrico é um...
- Uma Fórmula Para Calcular O Comprimento Da Elipse
Ao contrário de uma circunferência, não existe uma fórmula simples para calcular exatamente o comprimento (perímetro) de uma elipse. Neste post, veremos uma expressão aproximada em função do seu semieixo maior e de sua excentricidade. DeduçãoSeja...
- Integral De $\displaystyle \frac{\sqrt{16-x^2}}{4x^2}dx$
Às vezes surgem dúvidas de leitores que valem um post. A resolução desta integral é interessante e usa o método de substituição trigonométrica. Seja a integral: \begin{equation*} \int \frac{\sqrt{16-x^2}}{4x^2}dx = I \end{equation*} Vejam o artigo...
- Retas Perpendiculares
Veremos nesta postagem como determinar se duas retas são perpendiculares entre si, dados seus coeficientes angulares.Considere duas retas $r_1$ e $r_2$ não perpendiculares a nenhum dos eixos $x$ e $y$. Sejam $m_1$ e $m_2$ os coeficientes angulares das...
- Demonstração Da Relação Trigonométrica Fundamental
Nesta artigo, veremos como encontrar a relação trigonométrica fundamental no círculo trigonométrico utilizando o teorema de Pitágoras. Considere o círculo trigonométrico abaixo de raio unitário: O ponto $C$ é um ponto genérico sobre a circunferência...
Matemática
Desafio Resolvido
Parabéns
Romero Morais conseguiu resolver este desafio!
Resolução:

Temos:
$$N = P_y = m.g cos\theta$$
$$Fat = \mu . N = \mu . m.g.cos\theta$$
$$P_x = m.g.sen\theta$$
$$d$$ é a distância genérica percorrida pelo bloco.
Trabalho na ida:
$$\tau_T = \Delta{E_c}$$
$$\tau_{Fat} + \tau_{P_x} + \tau_{P_y} + \tau_N = E_{cF} - E_{cI}$$
$$\tau_{Fat} + \tau_{P_x} + E_{cF} = E_{cF} - E_{cI}$$
$$\tau_{Fat} + \tau_{P_x} = -E_{cI}$$
$$-\mu . m.g.cos\theta . d - m.g.sen\theta.d = -\frac{m.v^2}{2}$$
$$d = \frac{v^2}{2g(\mu cos\theta + sen\theta)}$$
Trabalho na volta:
$$\tau_T = \Delta{E_c}$$
$$\tau_{Fat} + \tau_{P_x} + \tau_{P_y} + \tau_N = E_{cF} - E_{cI}$$
$$\tau_{Fat} + \tau_{P_x} - E_{cI} = E_{cF} - E_{cI}$$
$$\tau_{Fat} +\tau_{P_x} = E_{cF}$$
$$-\mu.m.g.cos\theta.d + m.g.sen\theta.d = \frac{m.v^2}{2}(\div m)$$
$$-\mu.g.cos\theta \left[ \frac{V_0^2}{2g(\mu.cos\theta + sen\theta)}\right] + g.sen\theta \left[ \frac{V_0^2}{2g(\mu cos\theta + sen\theta)}\right] = \frac{V^2}{2}$$
$$V = V_0\sqrt{\frac{sen\theta - \mu cos\theta}{sen\theta + \mu cos\theta}}$$
Alternativa B.
- O Ciclo Trigonométrico
A definição das funções trigonométricas pode ser generalizada para um ângulo real qualquer através do ciclo trigonométrico. O ciclo trigonométrico é um...
- Uma Fórmula Para Calcular O Comprimento Da Elipse
Ao contrário de uma circunferência, não existe uma fórmula simples para calcular exatamente o comprimento (perímetro) de uma elipse. Neste post, veremos uma expressão aproximada em função do seu semieixo maior e de sua excentricidade. DeduçãoSeja...
- Integral De $\displaystyle \frac{\sqrt{16-x^2}}{4x^2}dx$
Às vezes surgem dúvidas de leitores que valem um post. A resolução desta integral é interessante e usa o método de substituição trigonométrica. Seja a integral: \begin{equation*} \int \frac{\sqrt{16-x^2}}{4x^2}dx = I \end{equation*} Vejam o artigo...
- Retas Perpendiculares
Veremos nesta postagem como determinar se duas retas são perpendiculares entre si, dados seus coeficientes angulares.Considere duas retas $r_1$ e $r_2$ não perpendiculares a nenhum dos eixos $x$ e $y$. Sejam $m_1$ e $m_2$ os coeficientes angulares das...
- Demonstração Da Relação Trigonométrica Fundamental
Nesta artigo, veremos como encontrar a relação trigonométrica fundamental no círculo trigonométrico utilizando o teorema de Pitágoras. Considere o círculo trigonométrico abaixo de raio unitário: O ponto $C$ é um ponto genérico sobre a circunferência...
